机器学习实战---用户流失预测
Python机器学习实战---用户流失预测
在过去的几年里,随着移动通讯设备和4G网络的普及,移动,电信,联通这三大通讯运营商之间的竞争愈发激烈,如何获取新用户?如何减少老用户流失?成了三大运营商头疼的问题,此次案例我们根据某个运营商的真实数据,通过数据分析和建立用户流失预测模型,来理解用户流失的一些重要规律。
本次案例分为这么几个部分:
- 数据导入及预处理
- 数据探索性分析
- 数据建模(采用决策树模型)
- 模型结果评价
- 决策树可视化
- 总结和思考
【数据导入及预处理】
1.数据来源:
本次案例数据取自“狗熊会”公众号上分享的手机客户流失数据,大家有兴趣可以关注一下这个公众号,上面有很多关于数据分析和建模的行业案例,并提供一些行业数据下载练习。
2.数据导入:
下载的文件为 ' CustomerSurvival.csv ',我们将数据导入到Python中:
# 导入分析用到的模块
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use('ggplot')
import seaborn as sns
sns.set_style('darkgrid')
sns.set_palette('muted')
# 导入csv文件
df = pd.read_csv('C:/Users/Administrator/Desktop/CustomerSurvival.csv',encoding='utf-8')
df.head()

3. 数据理解及变量解释
先看一下数据的概况:
df.info()

一共10个字段,且都是数值型变量,4975行数据,为便于分析,我们将中文字段改为英文:
df.columns = ['id','pack_type','extra_time','extra_flow','pack_change',
'contract','asso_pur','group_user','use_month','loss']
df.info()

变量含义及解释:
- id -- 用户的唯一标识
- pack_type -- 用户的月套餐的金额,1为96元以下,2为96到225元,3为225元以上
- extra_time -- 用户在使用期间的每月额外通话时长,这部分需要用户额外交费。数值是每月的额外通话时长的平均值,单位:分钟
- extra_flow -- 用户在使用期间的每月额外流量,这部分需要用户额外交费。数值是每月的额外流量的平均值,单位:兆
- pack_change -- 是否曾经改变过套餐金额,1=是,0=否
- contract -- 用户是否与联通签订过服务合约,1=是,0=否
- asso_pur -- 用户在使用联通移动服务过程中是否还同时办理其他业务,1=同时办理一项其他业务,2=同时办理两项其他业务,0=没有办理其他业务
- group_use -- 用户办理的是否是集团业务,相比个人业务,集体办理的号码在集团内拨打有一定优惠。1=是,0=否
- use_month -- 截止到观测期结束(2012.1-2014.1),用户使用联通服务的时间长短,单位:月
- loss -- 在25个月的观测期内,用户是否已经流失。1=是,0=否
---因变量是 'loss',是否流失,也是我们预测的目标值
---自变量分为三类:
# 连续型变量:extra_time,extra_flow, use_month
# 二元分类变量:pack_change,contract, group_use
# 多元分类变量:pack_type,asso_pur
4. 数据的预处理
先看一下各个字段是否有缺失:
df.isnull().any()
每个字段都没有缺失值,数据很完整,可以不作缺失值处理。
再判断一下用户的id是否唯一:
len(df.id.unique())
输出为:4975,与行数目一致,id没有重复值,每条记录都是唯一的。
【数据的探索性分析】
1. 数据的描述性统计:
df.describe()

可以看到extra_time和extra_flow有正负值,正数表示用户有额外的通话时长和流量,负数为用户在月底时剩余的套餐时长和流量。从四分位数中可看出超过一半的用户有额外通话时间,流量的话只有小部分用户超额使用了。另外其他的分类型变量在描述统计上并未发现有异常的地方。
在这里特别注意下use_month这个变量,数据的观测区间为2012.1-2014.1,一共25个月,且案例中关于流失的定义为:
超过一个月没有使用行为(包括通话,使用流量)的用户判定为流失。
在数据集中use_month小于25个月的基本都是流失状态,所以这个变量对于流失的预测并没有什么关键作用,后续导入模型时需剔除这个变量。
2. 变量的分布
首先看一下两个连续型变量:extra_time和extra_flow的数据分布:
plt.figure(figsize = (10,5))
plt.subplot(121)
df.extra_time.hist(bins = 30)
plt.subplot(122)
df.extra_flow.hist(bins = 30)

extra_time呈现的是右偏分布,extra_flow近似服从正态分布,与描述统计中的情况大致吻合
接下来看看分类型变量的分布:
fig,axes = plt.subplots(nrows = 2,ncols = 3, figsize = (10,6))
sns.countplot(x = 'pack_type',data = df,ax=axes[0,0])
sns.countplot(x = 'pack_change',data = df,ax=axes[0,1])
sns.countplot(x = 'contract',data = df,ax=axes[0,2])
sns.countplot(x = 'asso_pur',data = df,ax=axes[1,0])
sns.countplot(x = 'group_user',data = df,ax=axes[1,1])
sns.countplot(x = 'loss',data = df,ax=axes[1,2])
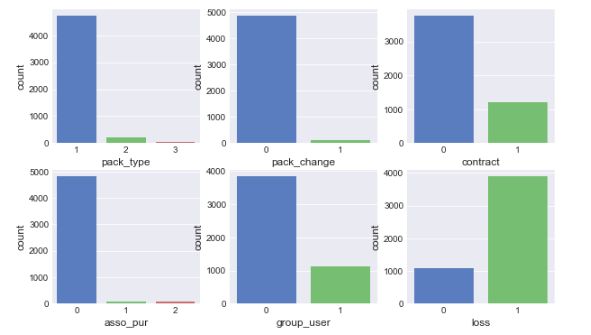
可以看到pack_type, pack_change, asso_pur的类型分布非常不均衡,例如asso_pur,办理过套餐外业务的用户数量极少,导致样本缺乏足够的代表性,可能会对模型的最终结果产生一定的影响。
3. 自变量与因变量之间的关系:
对于extra_time和extra_flow绘制散点图观察:
plt.figure(figsize = (10,6))
df.plot.scatter(x='extra_time',y='loss')
df.plot.scatter(x='extra_flow',y='loss')
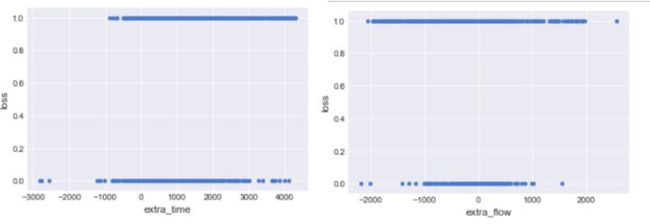
从散点图上似乎感觉两个自变量与是否流失并无关系,为了更好的展示其相关性,我们对extra_time和extra_flow进行分箱处理,再绘制条形图:
# 增加分箱后的两个字段
bin1 = [-3000,-2000,-500,0,500,2000,3000,5000]
df['time_label'] = pd.cut(df.extra_time,bins = bin1)
bin2 = [-3000,-2000,-500,0,500,2000,3000]
df['flow_label'] = pd.cut(df.extra_flow,bins = bin2)
# 观察一下分箱后的数据分布
time_amount = df.groupby('time_label').id.count().sort_values().reset_index()
time_amount['amount_cumsum'] = time_amount.id.cumsum()
time_amount['prop'] = time_amount.apply(lambda x:x.amount_cumsum/4975,axis =1)
flow_amount = df.groupby('flow_label').id.count().sort_values().reset_index()
flow_amount['amount_cumsum'] = flow_amount.id.cumsum()
flow_amount['prop'] = flow_amount.apply(lambda x:x.amount_cumsum/4975,axis=1)

---对extra_time进行累加统计,发现【-500,500】这个区间的用户占了80%,符合二八定律
---对extra_flow进行累加统计,发现【-500,500】占了95%,且(-500,0】的用户占80%,可以说只有小部分用户每月会超额使用流量。
绘制条形图:
sns.countplot(x = 'time_label',hue = 'loss',data =df)
sns.countplot(x = 'flow_label',hue = 'loss',data =df)
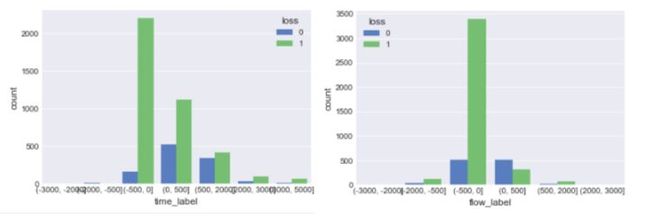
可以明显的看出用户使用的通话时间和流量越多,流失概率越低,这些超额使用的用户在用户分类中属于'高价值用户',用户粘性很高,运营商应该把重点放在这些用户身上,采取有效的手段预防其流失。
接着看其他自变量与流失的关系:
fig,axes = plt.subplots(nrows = 2,ncols = 3, figsize = (12,8))
sns.countplot(x = 'pack_type',hue = 'loss',data =df,ax = axes[0][0])
sns.countplot(x = 'pack_change',hue = 'loss',data =df,ax = axes[0][1])
sns.countplot(x = 'contract',hue = 'loss',data =df,ax = axes[0][2])
sns.countplot(x = 'asso_pur',hue = 'loss',data =df,ax = axes[1][0])
sns.countplot(x = 'group_user',hue = 'loss',data =df,ax = axes[1][1])
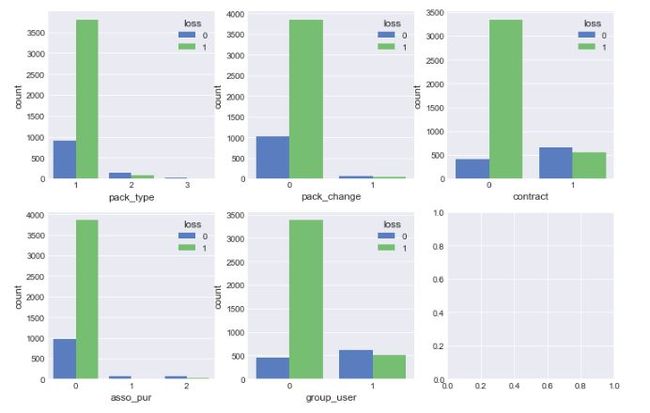
初步得出以下结论:
1).套餐金额越大,用户越不易流失,套餐金额大的用户忠诚度也高
2).改过套餐的用户流失的概率变小
3).签订过合约的流失比例较小,签订合约也意味着一段时间内(比如2年,3年)用户一般都不会更换运营商号码,可以说签订合约的用户比较稳定
4).办理过其它套餐业务的用户因样本量太少,后续再研究
5).集团用户的流失率相比个人用户低很多
最后通过相关性矩阵热力图观察各变量之间的相关性:
internal_chars = ['extra_time','extra_flow','pack_type',
'pack_change','contract','asso_pur','group_user','loss']
corrmat = df[internal_chars].corr()
f, ax = plt.subplots(figsize=(10, 7))
plt.xticks(rotation='0')
sns.heatmap(corrmat, square=False, linewidths=.5, annot=True)
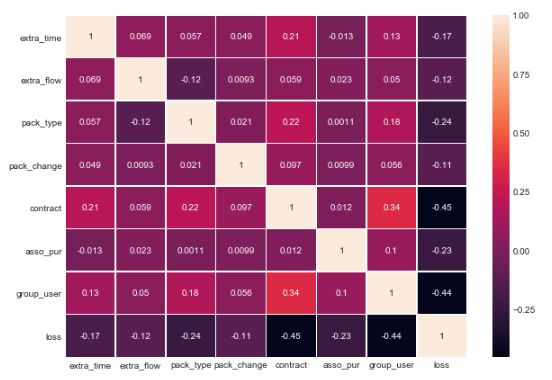
各自变量之间的相关性程度很低,排除了共线性问题。在对因变量的相关性上contract和group_user的系数相比其它变量较高,但也不是很强。
【数据建模】
因为自变量大多数为分类型,所以用决策树的效果比较好,而且决策树对异常值的敏感度很低,生成的结果也有很好的解释性。
1.特征的预处理
根据前面的探索性分析,并基于业务理解,我们决定筛选这几个特征进入模型:
extra_time,extra_flow,pack_type, pack_change, asso_pur
contract以及group_use,这些特征都对是否流失有一定的影响。
对于extra_time,extra_flow这两个连续型变量我们作数据转换,变成二分类变量,这样所有特征都是统一的度量。
df['time_tranf'] = df.apply(lambda x:1 if x.extra_time>0 else 0,axis =1)
df['flow_tranf'] = df.apply(lambda x:1 if x.extra_flow>0 else 0,axis =1)
df.head()
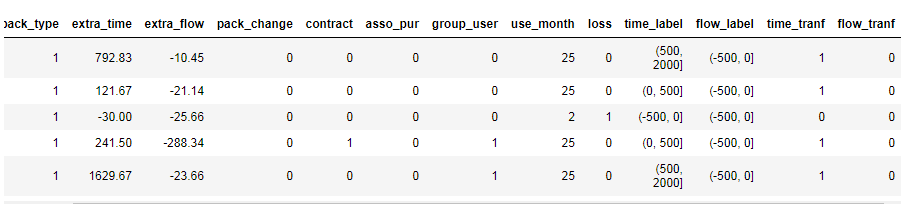
将没有超出套餐的通话时间和流量记为0,超出的记为1。
2. 建立自变量x, 因变量y的二维数组:
x = df.loc[:,['pack_type','time_tranf','flow_tranf','pack_change','contract','asso_pur','group_user']]
x = np.array(x)
x

y = df.loss
y = y[:, np.newaxis]
y

3. 拆分训练集和测试集,比例为7:3
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.3)
4. 建立决策树模型并拟合训练:
from sklearn import tree
clf = tree.DecisionTreeClassifier(criterion='gini', --设置衡量的系数
splitter='best', --选择分类的策略
max_depth=5, --设置树的最大深度
min_samples_split=10,--节点的最少样本数
min_samples_leaf=5 -- 叶节点的最少样本数
)
clf = clf.fit(x_train,y_train) -- 拟合训练
这里我们采用决策树中CART算法,基于gini系数进行分类,设置树的最大深度为5,区分一个内部节点需要的最少的样本数为10,一个叶节点所需要的最小样本数为5。
决策树最大的缺点是容易出现过拟合,所以我们先看一下模型对于训练数据和测试数据两者的评分情况:
train_score = clf.score(x_train,y_train) # 训练集的评分
test_score = clf.score(x_test,y_test) # 测试集的评分
'train_score:{0},test_score:{1}'.format(train_score,test_score)
可以看到针对训练集评分为0.874,针对测试集评分为0.867,两者近乎相等,说明模型较好的拟合训练集与测试集数据。
5.优化模型参数
对于决策树来说,可调参数有max_depth,min_samples_leaf,min_samples_split,
min_impurity_split等,一般用来解决模型过拟合的问题,也是一种“前剪枝”的方法。
我们以优化max_depth为例:
# 模型的参数调优--max_depth
# 创建一个函数,使用不同的深度来训练模型,并计算评分数据
def cv_score(d):
clf2 = tree.DecisionTreeClassifier(max_depth=d)
clf2 = clf2.fit(x_train,y_train)
tr_score = clf2.score(x_train,y_train)
cv_score = clf2.score(x_test,y_test)
return (tr_score, cv_score)
# 构造参数范围,在这个范围内构造模型并计算评分
depths = range(2,15)
scores = [cv_score(d) for d in depths]
tr_scores = [s[0] for s in scores]
cv_scores = [s[1] for s in scores]
# 找出交叉验证数据集最高评分的那个索引
best_score_index = np.argmax(cv_scores)
best_score = cv_scores[best_score_index]
best_param = depth[best_score_index]
print('best_param : {0},best_score: {1}'.format(best_param,best_score))
最优的深度为5,最佳评分为0.868,这与我们一开始设置的最大深度相同。
我们还可以将模型参数与评分的关系画出来,更可以清楚地看到其变化规律:
plt.figure(figsize = (4,2),dpi=150)
plt.grid()
plt.xlabel('max_depth')
plt.ylabel('best_score')
plt.plot(depths, cv_scores,'.g-',label = 'cross_validation scores')
plt.plot(depths,tr_scores,'.r--',label = 'train scores')
plt.legend()
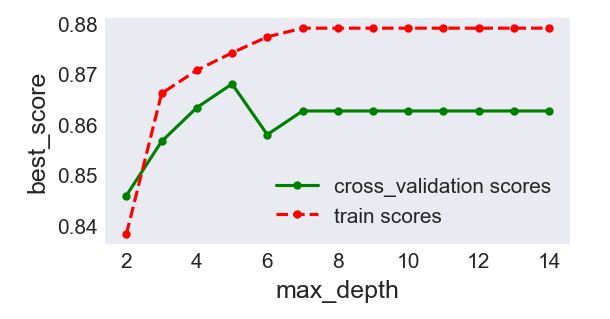
在生成的图中可以看出当深度为5时,交叉验证数据集的评分与训练集的评分比较接近,且两者的评分比较高,当深度超过5以后,俩者的差距变大,交叉验证数据集的评分变低,出现了过拟合情况。
【模型结果评价】
可以调用Scikit-learn的classification_report模块,生成分析报告。
from sklearn.metrics import classification_report
print(classification_report(y_test, y_pred))
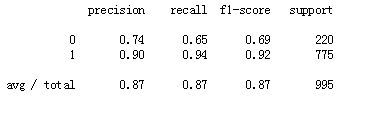
这里说一下评价模型好坏的指标:
精确率,召回率,F1,AUC和ROC曲线,KS值。
以这个用户流失预测模型为例,它是一个有监督的二分类模型,我们把模型应用在测试集数据后会产生一个“预测表现”和“实际表现”,形成一个混淆矩阵:
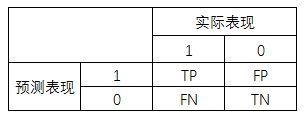
精确率 = TP/(TP+FP) :在预测为流失的用户中,预测正确的(实际也是流失)用户占比
召回率 = TP/(TP+FN) : 在实际为流失的用户中,预测正确的(预测为流失的)用户占比
F1值为精确率和召回率的调和均值,相当于这两个的综合评价指标。
通过输出的分析报告可以得出建立的预测模型的精确率为0.87,说明在预测为流失的用户中,实际流失的用户占87%,召回率也为0.87,说明实际为流失的用户中,预测为流失的占87%,F1值为0.87,说明模型的综合评价还不错。
ROC曲线和AUC值经常作为衡量一个模型拟合程度的指标,ROC曲线是对多个混淆矩阵的结果组合,每个混淆矩阵都会计算TPR(召回率)和FPR,FPR为实际为不流失的用户中,预测为流失的占比(FP/(FP+TN)),以FPR为x轴,TPR为y轴,就得到了ROC曲线图:
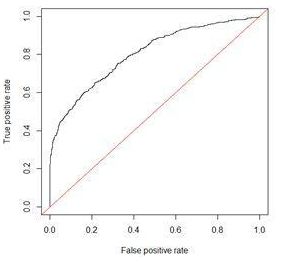
而AUC的值为ROC曲线下面的面积,如果这个模型十分精确,则ROC曲线经过(0,1)点,且AUC的值为1,不过在实际情形中,不会出现这么精确的模型,一般AUC的值在0.5到1之间,如果AUC=0.5或小于0.5,说明这个模型很差。
画ROC曲线的代码如下(小伙伴们可以直接copy跑一下):
from sklearn import svm, datasets
from sklearn.metrics import roc_curve, auc # 计算roc和auc
from sklearn import cross_validation
random_state = np.random.RandomState(0)
n_samples, n_features = x.shape
X = np.c_[x, random_state.randn(n_samples, 200 * n_features)]
X_train, X_test, y_train2, y_test2 = cross_validation.train_test_split(X, y, test_size=.2,random_state=0)
svm = svm.SVC(kernel='linear', probability=True,random_state=random_state)
y_score = svm.fit(X_train, y_train2).decision_function(X_test)
fpr,tpr,threshold = roc_curve(y_test, y_score) # 计算真正率和假正率
roc_auc = auc(fpr,tpr) # 计算auc的值
plt.figure()
lw = 2
plt.figure(figsize=(6,6))
plt.plot(fpr, tpr, color='darkorange',
lw=lw, label='ROC curve (area = %0.2f)' % roc_auc) ###假正率为横坐标,真正率为纵坐标做曲线
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()
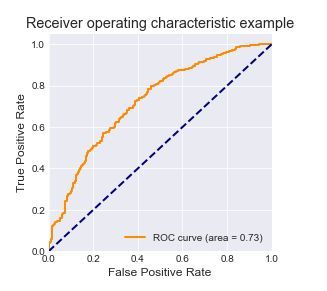
AUC的值为0.73,模型的拟合程度还有一定的提升空间。
除此之外,在评价模型时也会用到KS值,KS =max(TPR - FPR),KS值可以反映模型的最优区分效果。
在实际业务中,选择哪个指标作为依据是要根据应用场景的,比如用户流失预测案例,我们会更关注召回率,模型的目的要尽可能的找全实际将流失的用户,也就是实际流失的用户中,模型能预测到多少,这是评价这个模型结果的关键指标。所以在今后模型的优化中,我们要尽可能提高TPR。
【决策树可视化】
决策树最大的好处是可以生成可视化的树结构,有助于我们对模型的理解。
在可视化前我们需要下载graphviz并安装,安装完后打开将其bin目录添加到电脑的环境变量中,关于如何添加环境变量大家自行百度,操作非常简单。
接下来导入graphviz模块,绘制树结构并导出到外部文件。
from sklearn.tree import export_graphviz
with open('D:/dataset/userloss.dot','w')as f:
f=export_graphviz(clf,
feature_names=['pack_type','time_tranf','flow_tranf'
,'pack_change','contract','asso_pur','group_user'],
class_names=['loss','not loss'],
filled=True, rounded=True,
special_characters=True,
out_file=f
)
执行这个程序后会在指定的文件夹里生成一个dot文件,我们需要通过cmd命令进入到这个文件所在的目录下,然后通过‘ dot -Tpng 文件名 -o 输出文件名’的形式进行转化,将dot文件转为png的图片格式:
最后的可视化结果如下图:

放大看一下:
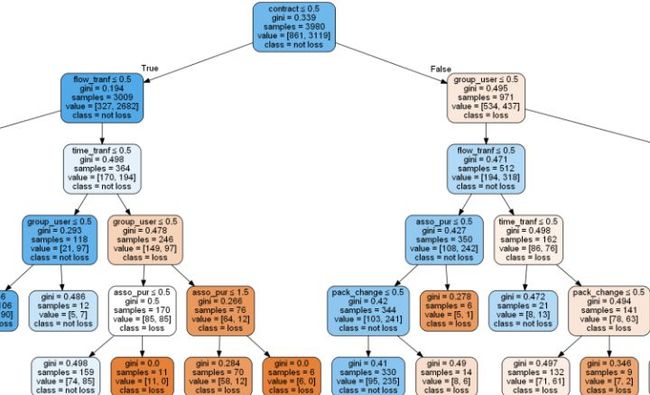
因为之前建模的时候设置的深度为5,所以树有5层,里面包含了分类的特征选择和对应的样本数,非常清晰直观。
【总结和思考】
- 从数据的探索性分析中我们可以看出,运营商关注的重点应该放在那些高价值的用户上,比如使用通话和流量比较多的,套餐金额比较大的这些用户。应采取相应的运营策略预防其流失,并且可以分析用户流失的主要原因,是优惠福利不满意还是竞争对手在某些方面比自己有优势。在这个通讯行业激烈竞争的时代,且手机用户数量已基本饱和,维护老用户比获取新用户更容易。
- 在预测模型的优化上,还有很多的改进之处,比如调整决策树的参数,特征的精细化筛选,或者采用多种算法进行模型评估。而且这个数据还有很多东西值得分析挖掘,用户的分类,用户的生命周期分析,各变量之间的交叉分析等等,今后还需对这个项目进行多方面的改进。
今天的用户流失预测案例就写到这啦~~bye。。