数据结构与算法 -- 树结构与图结构
树的概念
形式化定义：算法的集合树(Tree)是由一个或多个结点组成的有限集合T，其中有一个特定的称为根的结点；其余结点可分为(m≥0)个互不相交的有限集T1,T2,T3,…,Tm，每一个集合本身又是一棵树，且称为根的子树。
逻辑结构：
树的表示：
- 图形表示法
- 表表示法：(A(B(E,F),C(G),D(H,I,J)))
树的术语：
- 结点的度：结点子树个数为结点的度
- 树的度：树中结点度的最大值
- 森林：0棵或多棵不相交的树的集合
树的存储结构可以采用具有多个指针域的多重链表，结点中指针域的个数应由树的度来决定。
二叉树
定义：二叉树是n（n≥0）个结点的有限集，它或者是空集（n=0），或者由一个根结点及两棵不相交的左子树和右子树组成。
特点：
- 在二叉树中，不存在度大于2的结点；
- 二叉树是有序树（树为无序树），其子树的顺序不能颠倒。
基本形态：二叉树有五种不同的形态。
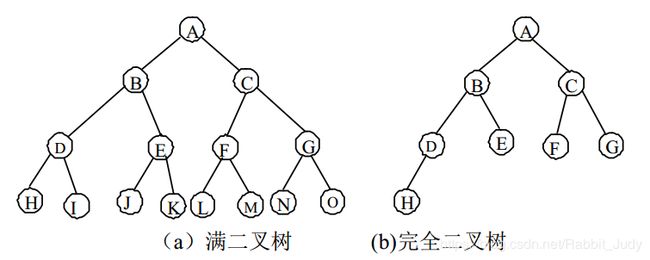
满二叉树：深度为k具有
个结点的二叉树，称为满二叉树。
完全二叉树：如果一棵具有n个结点的深度为k的二叉树，它的每一个结点都与深度为k的满二叉树中编号为1~n的结点一一对应，则称这棵二叉树为完全二叉树。完全二叉树又称为顺序二叉树。
性质：
-
若二叉树的层数从1开始，则二叉树的第k层结点数，最多为
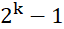个（k≥1）。 - 深度（高度）为k的二叉树最多结点数为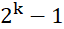（k≥1）。
- 若对任意一棵二叉树，如果叶子结点(度为0)个数为
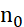，度为2的结点个数为
，则有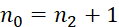
。 - 具有n个结点的完全二叉树高度为
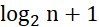或
。
遍历二叉树：令L,R,T分别代表二叉树的左子树、右子树、根结点，若规定二叉树中必须先左后右(左右顺序不能颠倒)，则只有TLR、LTR、LRT三种遍历规则。
- TLR称为前根遍历(或前序遍历、先序遍历、先根遍历)
- LTR称为中根遍历(或中序遍历)
- LRT称为后根遍历(或后序遍历)
二叉树的存储结构:
- 顺序存贮结构：将一棵二叉树按完全二叉树顺序存放到一个一维数组中。
- 二叉链表存贮结构：将对于非完全二叉树，宜采用链式存储结构。
二叉树例程：
/**
* 二叉树
* @author wangfei
*
*/
public class TestBinaryTree {
public static void main(String[] args) {
//创建一棵树
BinaryTree binaryTree = new BinaryTree();
//创建一个根节点
Node root = new Node(1);
//把根节点赋值给树
binaryTree.setRoot(root);
//创建一个左节点
Node rootL = new Node(2);
//把新创建的节点设置为根节点的子节点
root.setLeftNode(rootL);
//创建一个右节点
Node rootR = new Node(3);
//把新创建的节点设置为根节点的子节点
root.setRightNode(rootR);
//为第二层创建两个子节点
root.setLeftNode(new Node(4));
root.setRightNode(new Node(5));
//前序遍历树
binaryTree.frontShow();
System.out.println("===========================");
//中序遍历树
binaryTree.midShow();
System.out.println("===========================");
//后序遍历树
binaryTree.afterShow();
System.out.println("===========================");
//前序查找
Node result = binaryTree.frontSearch(5);
System.out.println(result);
System.out.println("===========================");
//删除一个子树
binaryTree.delete(4);
binaryTree.frontShow();
}
}
public class BinaryTree {
Node root;
//设置根节点
public void setRoot(Node root) {
this.root = root;
}
//获取根节点
public Node getRoot(Node root) {
return root;
}
//前序遍历
public void frontShow() {
if(root!=null) {
root.frontShow();
}
}
//中序遍历
public void midShow() {
if(root!=null) {
root.midShow();
}
}
//后序遍历
public void afterShow() {
if(root!=null) {
root.afterShow();
}
}
//前序查找
public Node frontSearch(int i) {
return root.frontSearch(i);
}
//删除一个子树
public void delete(int i) {
if(root.value==i) {
root = null;
}else {
root.delete(i);
}
}
}
public class Node {
//节点的权
int value;
//左儿子
Node leftNode;
//右儿子
Node rightNode;
public Node(int value) {
this.value = value;
}
//设置左儿子
public void setLeftNode(Node leftNode) {
this.leftNode = leftNode;
}
//设置右儿子
public void setRightNode(Node rightNode) {
this.rightNode = rightNode;
}
//前序遍历
public void frontShow() {
//先遍历当前节点内容
System.out.println(value);
//左节点
if(leftNode!=null) {
leftNode.frontShow();
}
//右节点
if(rightNode!=null) {
rightNode.frontShow();
}
}
//中序遍历
public void midShow() {
//左子节点
if(leftNode!=null) {
leftNode.midShow();
}
//当前节点
System.out.println(value);
//右子节点
if(rightNode!=null) {
rightNode.midShow();
}
}
//后序遍历
public void afterShow() {
//左子节点
if(leftNode!=null) {
leftNode.afterShow();
}
//右子节点
if(rightNode!=null) {
rightNode.afterShow();
}
//当前节点
System.out.println(value);
}
//前序查找
public Node frontSearch(int i) {
Node target = null;
//对比当前节点的值
if(this.value==i) {
return this;
//当前节点的值不是要查找的节点
}else {
//查找左儿子
if(leftNode!=null) {
//查不到的话，target还是null
target = leftNode.frontSearch(i);
}
//如果不为空，说明在左儿子中已经找到
if(target!=null) {
return target;
}
//查找右儿子
if(rightNode!=null) {
target = rightNode.frontSearch(i);
}
}
return target;
}
//删除节点
public void delete(int i) {
Node parent = this;
//判断左儿子
if(parent.leftNode!=null && parent.leftNode.value==i) {
parent.leftNode = null;
return;
}
//判断右儿子
if(parent.rightNode!=null && parent.rightNode.value==i) {
parent.rightNode = null;
return;
}
//递归检查并删除左儿子
parent = leftNode;
if(parent!=null) {
parent.delete(i);
}
//递归检查并删除右儿子
parent = rightNode;
if(parent!=null) {
parent.delete(i);
}
}
}
图的概念
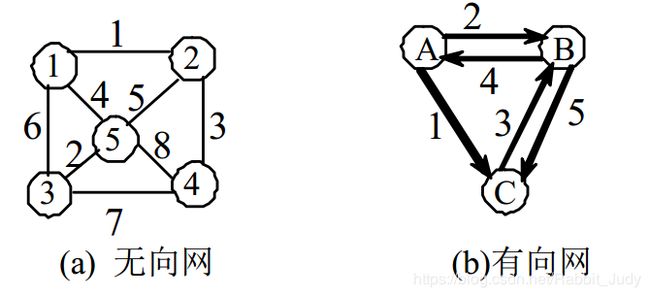
定义：图是由顶点集V和顶点间的关系集合E（边的集合）组成的一种数据结构，可以用二元组定义为：G=（V，E）。
有向图和无向图：为新的对话框类添加方在图中，若用箭头标明了边是有方向性的，则称这样的图为有向图，否则称为无向图。
上图可描述为：
G1=(V1,E)，V1={a,b,c,d},E1={(a,b),(a,c),(a,d),(b,d),(c,d)}
G2=(V2,E2)， V2={1,2,3}，E2={<1,2>,<1,3>,<2,3>,<3,1>}
度、入度、出度：具有n个顶点，在图中，一个顶点依附的边或弧的数目，称为该顶点的度。在有向图中，一个顶点依附的弧头数目，称为该顶点的入度。一个顶点依附的弧尾数目，称为该顶点的出度，某个顶点的入度和出度之和称为该顶点的度。
另外，若图中有n个顶点，e条边或弧，第i个顶点的度为di，则有
权：若在图的边或弧中给出相关的数，称为权。权可以代表一个顶点到另一个顶点的距离，耗费等，带权图一般称为网。
连通图和非连通图：在无向图中，若任意两个顶点都是连通的，则称此无向图为连通图，否则称为非连通图。
强连通图和非强连通图：在有向图中，若图中任意两个顶点都是连通的，则称此有向图为强连通图，否则称为非强连通图
图的邻接矩阵
定义：
在邻接矩阵表示中，除了存放顶点本身信息外，还用一个矩阵表示各个顶点之间的关系。若（i，j）∈E(G)或〈i，j〉∈E(G),则矩阵中第i行第j列元素值为1，否则为0。
从无向图的邻接矩阵可以得出如下结论：
- 矩阵是对称的；
- 第i行或第i列1的个数为顶点i的度；
- 矩阵中1的个数的一半为图中边的数目；
- 很容易判断顶点i和顶点j之间是否有边相连（看矩阵中i行j列值是否为1）。
从有向图的邻接矩阵可以得出如下结论：
- 矩阵不一定是对称的；
- 第i行中1的个数为顶点i的出度；
- 第i列中1的个数为顶点i的入度；
- 矩阵中1的个数为图中弧的数目；
- 很容易判断顶点i和顶点j是否有弧相连。
图的邻接表
定义：将每个结点的边用一个单链表链接起来，若干个结点可以得到若干个单链表，每个单链表都有一个头结点，所有头结点组成一个一维数组，称这样的链表为邻接表。
从无向图的邻接表可以得到如下结论：
- 第i个链表中结点数目为顶点i的度；
- 所有链表中结点数目的一半为图中的边数；
- 占用的存储单元数目为n+2e（e：边数）。
从有向图的邻接表可以得到如下结论：
- 第i个链表中结点数目为顶点i的出度；
- 所有链表中结点数目为图中弧数；
- 占用的存储单元数目为n+e。
深度优先搜索思想：深度优先搜索遍历类似于树的先序遍历。假定给定图G的初态是所有顶点均未被访问过，在G中任选一个顶点i作为遍历的初始点，则深度优先搜索遍历可定义如下：
- 首先访问顶点i，并将其访问标记置为访问过，即visited[i] =1；
- 然后搜索与顶点i有边相连的下一个顶点j，若j未被访问过，则访问它，并将j的访问标记置为访问过，visited[j]=1，然后从j开始重复此过程，若j已访问，再看与i有边相连的其它顶点；
- 若与i有边相连的顶点都被访问过，则退回到前一个访问顶点并重复刚才过程，直到图中所有顶点都被访问完止。
广度优先搜索的思想：广度优先搜索遍历类似于树的按层次遍历。设图G的初态是所有顶点均未访问，在G中任选一顶点i作为初始点，则广度优先搜索的基本思想是：
- 首先访问顶点i，并将其访问标志置为已被访问，即visited[i]=1；
- 接着依次访问与顶点i有边相连的所有顶点W1，W2，…，Wt；
- 然后再按顺序访问与W1，W2，…，Wt有边相连又未曾访问过的顶点；
- 依此类推，直到图中所有顶点都被访问完为止。
图结构例程：
/**
* 图
* @author wangfei
*
*/
public class Graph {
private Vertex[] vertexs;
private int currentSize;
public int[][] adjMat;
private MyStack stack = new MyStack();
//当前遍历的下标
private int currentIndex;
public Graph(int size) {
vertexs = new Vertex[size];
adjMat = new int[size][size];
}
/**
* 向图中加入一个顶点
* @param v
*/
public void addVertex(Vertex v) {
vertexs[currentSize++] = v;
}
/**
* 向相邻顶点添加连接线
* @param v1
* @param v2
*/
public void addEdge(String v1, String v2) {
//找出两个顶点的下标
int index1 = 0;
for(int i=0; i/**
* 顶点类
* @author wangfei
*
*/
public class Vertex {
private String value;
public boolean visited;
public String getValue() {
return value;
}
public void setValue(String value) {
this.value = value;
}
public Vertex(String value) {
super();
this.value = value;
}
@Override
public String toString() {
return value;
}
}
public class MyStack {
//栈的底层我们使用数组来存储数据
int[] elements;
public MyStack() {
elements = new int[0];
}
//压入元素
public void push(int element) {
// 创建一个新的数组
int[] newArr = new int[elements.length + 1];
// 把原数组中的元素复制到新数组中
for (int i = 0; i < elements.length; i++) {
newArr[i] = elements[i];
}
// 把添加的元素放入新数组中
newArr[elements.length] = element;
// 使用新数组替换旧数组
elements = newArr;
}
//取出栈顶元素
public int pop() {
//栈中没有元素
if(elements.length==0) {
throw new RuntimeException("stack is empty");
}
//取出数组的最后一个元素
int element = elements[elements.length-1];
//创建一个新的数组
int[] newArr = new int[elements.length-1];
//原数组中除了最后一个元素的其它元素都放入新的数组中
for(int i=0;i