Predicting Multi-step Citywide Passenger Demands Using Atention-based Neural Networks
1. 背景
这是一篇发表在 WSDM 2018上的文章,其所要解决的问题同前篇文章介绍的一样,都是解决流量预测的问题。只是这篇论文是预测接下来几个时刻的流量(Multi-step)。而为什么作者要提出Multi-step demand prediction呢?
作者认为,Multi-step demand prediction不仅能够体现流量变化的趋势,而且能够表达处全局的变化,从而能够避免因临时突发的需求变化而导致整体预测失误。什么意思呢? 比如 t 1 , t 2 , t 3 , t 4 t_1,t_2,t_3,t_4 t1,t2,t3,t4时刻需求分别为 5 , 10 , 20 , 30 5,10,20,30 5,10,20,30:如果是按照单步(next-step)预测,由于在 t 1 t_1 t1时刻时需求量很小,则会把多余的资源分配到其它地方去,而又由于接下来的几个时刻需求量直线上升,又需要重其它地方紧急的分配资源过来;而如果是按照多步预测的话,在 t 1 t_1 t1时刻就能知道后续几个时刻的需求变化趋势,在 t 1 t_1 t1时刻分配资源时就尽可能的保留一些(若有多余资源尽可能保留),因为 t 2 , t 3 , t 4 t_2,t_3,t_4 t2,t3,t4时刻马上就要用到,而单步预测做不到这一点。
同时,作者还认为需求量(pickup demands)同dropoff demands时紧密相关的,因此需要将两者结合起来构成两个通道。(注:pickup demands 指的是从A地出发的流量,dropoff demands 指的是到达A地的流量;)
1.1 数据预处理
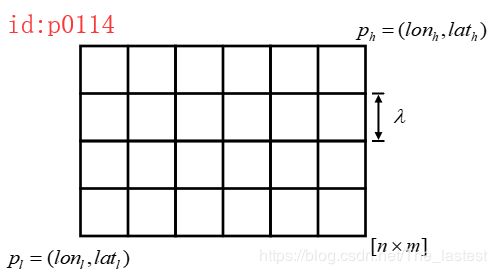
作者在这篇文章中使用的是出租车和单车数据,首先仍旧是将整个城市划分为若干个 m × n m\times n m×n的方格,且通过一个超参数 λ \lambda λ来控制方格的宽度。如图p0110所示,A、B、C分别表示三个区域,红色的通道表示pickup demand,蓝色部分表示dropoff demand。从表©中可以看出上一时刻的dropoff demand 会影响到下一时刻的pickup demand。
1.2 问题定义
作者在论文的第三部分给出了三个定义,分别是Grid Map, Pickup/Dropff Demand Maps, Multi-step Citywide Demands Precition。简单来说,这三个定义分别做了如下工作:
- Grid Map: 定义网格,将整个城市划分为若干个格子,且有一个能够控制网格宽度的参数 λ \lambda λ ,同时将所有的原始数据都映射到网格中;
-
统计每个时间间隔内,各个网格中的pickup/dropoff demand;
-
定义需要解决的问题;
若对数据的处理有疑惑可参考这篇论文中类似的处理方式
2. 网络模型
2.1 idea
作者在论文的摘要部分的第一段主要提到说单步预测不如多步预测,多步预测更能从全局的角度来考虑问题,使得从长远来看有着更优解而不是短期的一步(有点类似于强化学习的理念);然后第二段就介绍了论文中所用到的模型: Seq2Seq,Attention 和ConvLSTM。(若不熟悉这三个模型,可简单参考此处Seq2Seq, Attention,ConvLSTM)我们知道在Seq2Seq中使用注意力机制的话,需要用到所谓的’thought vector’,也就是根据编码时候各个时刻的输出和当前解码时刻的输出所计算出来的一个向量。 但是在这篇论文中,作者使用的却是 由"representative demand tensors"(下文称作 A A A )计算出的向量。那这个 A A A又是何方神圣呢?
我们都知道,对于任何(个人目前所知)场景下的流量预测问题,如某地区的订单量、人流量、车流量等等都是存在若干种规律的。在论文中,作者的观点认为对于某个任务来说,假如其存在 K K K种潜在规律,那么在解码预测的时候给输入作用上某种规律,则结果应该会更好。值得一提的是,在翻译模型的Seq2Seq模型种,注意力是作用在记忆单元的输出上的,而在这篇论文种却是作用在输入上的。
2.2 模型
整体的网络结构图如p0111所示,其中:
-
(1)编码: 对于Encoder部分主要包括了两个部分:CNN和ConvLSTM。对于输入的demand tesors { M 1 , ⋯ M N } \{\mathcal{M}_1,\cdots\mathcal{M}_N\} {M1,⋯MN},首先每一个demand tensor M t \mathcal{M}_t Mt都通过 L L L层的卷积处理得到 I t , L e I^e_{t,L} It,Le(,因此对于 N N N个demand tesors来说将得到 { I t , L e } t = 1 N \{I^e_{t,L}\}^N_{t=1} {It,Le}t=1N;接着,将 { I t , L e } t = 1 N \{I^e_{t,L}\}^N_{t=1} {It,Le}t=1N喂给多层的ConvLSTM网络。
-
(2)注意力: 为了能更清楚的说明解码部分,我们先来谈注意力;
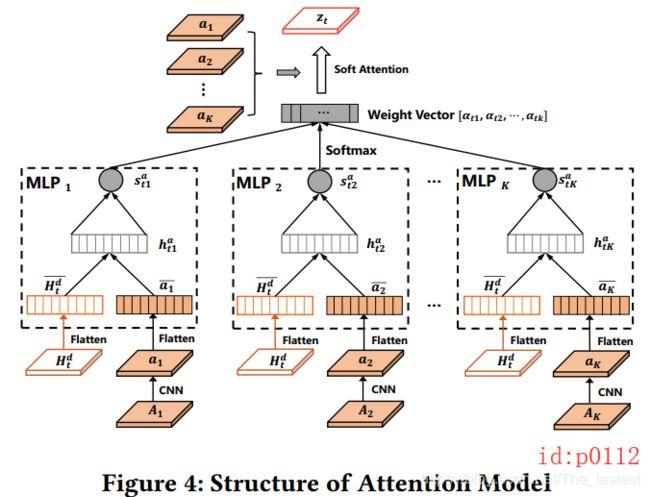
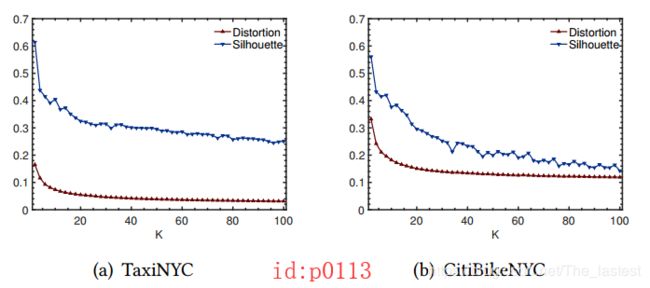
如图p0112所示为整个注意力计算的结构图;首先需要说明的就是这个demand tensors { A k } k = 1 K \{A_k\}^K_{k=1} {Ak}k=1K,没错这也就是我们在idea部分说到”representative demand tensor“,它也是一个3维的张量,其中 ( A k ) i j (A_k)_{ij} (Ak)ij 反映了区域 g i j g_{ij} gij受某种潜在规律作用后的pickup 和dropoff demands。什么意思呢?个人的理解是:由于每种流量数据都可能暗含着 K K K种潜在的变化规律,而 { A k } k = 1 K \{A_k\}^K_{k=1} {Ak}k=1K这 K K K个张量是最直接最能体现这 K K K种规律的张量。根据论文种的介绍, { A k } k = 1 K \{A_k\}^K_{k=1} {Ak}k=1K 就是将原始数据集聚类后的 K K K个簇中心。可能熟悉聚类算法的同学会问,那 K K K是怎么来的呢?原文中的实验部分提到,一个恰当的 K K K值应该满足较低的簇间距离(下图的distortion)和较高的轮廓系数(下图中的Silhouette);基于这样的原则作者在两个数据集上的 K K K分别是16和32.
在有了 { A } k \{A\}_k {A}k之后,进一步对其进行卷积操作得到 a k a_k ak;接着将编码部分最后一时刻的隐含状态 H t d H^d_t Htd分别同 a k a_k ak通过一个2层神经网络进行相似度计算得到 α t 1 , α t 2 , ⋯ α t k \alpha_{t1},\alpha_{t2},\cdots\alpha_{tk} αt1,αt2,⋯αtk,最后再进一步得到注意力向量 z t z_t zt。(具体计算公式如下:)
h t k a = f ( W h a H t − 1 d ‾ + W a a k ‾ + b h a ) , ∀ k ∈ [ 1 , K ] s t k a = f ( W s a h t k a ) , ∀ k ∈ [ 1 , K ] a t k = e x p ( s t k a ) ∑ k = 1 K e x p ( s t k a ) , ∀ k ∈ [ 1 , K ] z t = ∑ k = 1 K a t k a k \begin{aligned} h^a_{tk}&=f(W^a_h\overline{H^d_{t-1}}+W_a\overline{a_k}+b^a_h),\forall k\in[1,K]\\[2ex] s^a_{tk}&=f(W_s^ah^a_{tk}),\forall k \in[1,K]\\[2ex] a_{tk}&=\frac{exp(s^a_{tk})}{\sum^K_{k=1}exp(s^a_{tk})},\forall k \in[1,K]\\[2ex] z_t&=\sum^K_{k=1}a_{tk}a_k \end{aligned} htkastkaatkzt=f(WhaHt−1d+Waak+bha),∀k∈[1,K]=f(Wsahtka),∀k∈[1,K]=∑k=1Kexp(stka)exp(stka),∀k∈[1,K]=k=1∑Katkak
- (3)解码:清楚了注意力部分后,对于解码部分就容易得多了,计算公式如下:
i t d = σ ( W z i d ∗ z t + W h i d ∗ H t − 1 d + b i d ) f t d = σ ( W z f d ∗ z t + W h f d ∗ H t − 1 d + b f d ) o t d = σ ( W z o d ∗ z t + W h o d ∗ H t − 1 d + b o d ) C t d = f t d ∘ C t − 1 d + i t d ∘ t a n h ( W z c d ∗ z t + W h c d ∗ H t − 1 d + b c d ) H t d = o t d ∘ t a n h ( C t d ) \begin{aligned} i^d_t&=\sigma(W^d_{zi}*z_t+W^d_{hi}*H^d_{t-1}+b^d_i)\\[2ex] f^d_t&=\sigma(W^d_{zf}*z_t+W^d_{hf}*H^d_{t-1}+b^d_f)\\[2ex] o^d_t&=\sigma(W^d_{zo}*z_t+W^d_{ho}*H^d_{t-1}+b^d_o)\\[2ex] C^d_t&=f^d_t\circ C^d_{t-1}+i^d_t\circ tanh(W^d_{zc}*z_t+W^d_{hc}*H^d_{t-1}+b^d_c)\\[2ex] H^d_t&=o^d_t\circ tanh(C^d_t) \end{aligned} itdftdotdCtdHtd=σ(Wzid∗zt+Whid∗Ht−1d+bid)=σ(Wzfd∗zt+Whfd∗Ht−1d+bfd)=σ(Wzod∗zt+Whod∗Ht−1d+bod)=ftd∘Ct−1d+itd∘tanh(Wzcd∗zt+Whcd∗Ht−1d+bcd)=otd∘tanh(Ctd)
从公式中可以看到,ConvLSTM的输入除了上一时刻的 H t − 1 d , C t − 1 d H^d_{t-1},C^d_{t-1} Ht−1d,Ct−1d之外,还有的就是当前时刻的注意力向量。在得到多个时刻的输出 H t d H^d_t Htd 后,再经过多层(同编码部分的CNN一样)的卷积作为整个模型的输出。
3. 总结
对于论文中的需求预测问题,首先作者认为pickup demands应该是与收到dropoff demands影响的,应该将两者进行结合;其次作者认为对于流量预测问题应该从全局最优的角度来进行考虑,故而提出了multi-step;最后作者还认为每种流量数据都可能存在多种潜在的规律(latent mobility patterns),并且可以将这种潜在的规律作用于解码时的输入来提高预测结果。
4.交流
问: @hello怪:能不能解释一下这里用attention的原因? 大体感觉上是寻找离 h h h最近的一个聚类中心 a i a_i ai, 用 a i a_i ai代替 h h h的值(虽然都是soft),但是不太清楚为什么要这样做。一般的attention系数 α \alpha α不是应当和MLP输出的值做加权平均吗?为什么这个模型里面 α \alpha α和聚类中心去做加权平均了呢?
答:
第一点,为什么要用attention? 我在上面的博文中说到,“我们都知道,对于任何(个人目前所知)场景下的流量预测问题,如某地区的订单量、人流量、车流量等等都是存在若干种规律的。在论文中,作者的观点认为对于某个任务来说,假如该数据集存在K种潜在规律,那么在解码预测的时候给输入作用上某种规律,则结果应该会更好。“ 什么意思呢?由于这类数据通常存在着规律特性(且是多种,设为 K K K种),并且假如我们能找到这 K K K种规律,然后将符合当前时刻输出的规律再作用于当前时刻,这样就会使得预测的结果更准确。而聚类的作用就是用来找这 K K K种规律,Attension则是用来从 K K K种规律中找最符合当前时刻输出的那种规律特性。
第二点,一般的attention系数 α \alpha α不是应当和MLP输出的值做加权平均吗?为什么这个模型里面 α \alpha α和聚类中心去做加权平均了呢? 这个问题是你没描述清楚还是我没理解到位? 一般的attention中, α \alpha α通过MLP得到,然后再将 a l p h a alpha alpha作用于MLP的输入(文中是 a 1 , a 2 , . . . , a k a_1,a_2,...,a_k a1,a2,...,ak,也就是MLP的输入用CNN提取一次特征后的结果,形式上也差不多),你可以再仔细看看论文中的网络结构,再交流! 祝好!