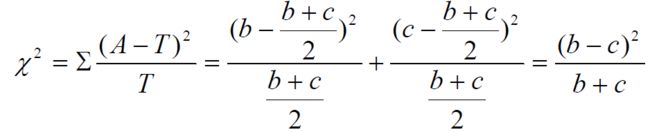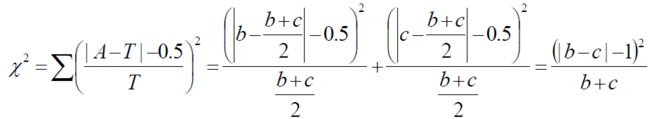统计推断——假设检验——卡方检验

一、独立样本四格表资料的检验

问题的提出：

检验：比较两个样本均数的差别是否有统计学意义。

检验：多个样本均数之间的差别是否有统计学意义。

在医学研究中，还常需对比两组或多组定性变量（如检验结果：愈合和未愈合）资料之间的差别，例如比较两种或多种治疗方法的治愈率是否不同。该怎么办？

1.1 检验的基本思想

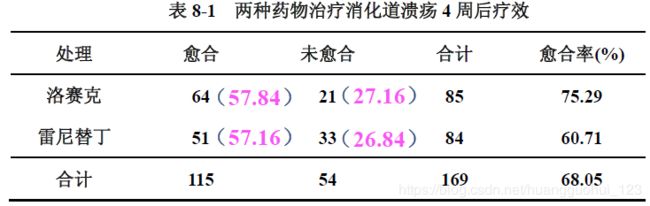
 假设两种药物治疗的愈合率是相等的（成立的条件下），那么这两种药物的愈合率就可以进行合并估计。即愈合的人数相加等于115人，合计的人数相加等于169人，愈合率115/169=68.05%。也就是说如果两组总体愈合率相等这个前提是成立的，那么68.05%就是对总体愈合率的最好估计，因为样本量更大了。

以此算成立的条件下，两种药物理论上的愈合人数（期望愈合数）和未愈合人数，如洛赛克的愈合人数等于85*68.05%=57.84，未愈合人数等于85*（1-85%）等于27.16。

即求实际数和理论数的相对误差（不吻合值），在进行累加，如果累加误差接近0，就说样本支持。分子平方的意义在于避免正的不吻合值和负的不吻合值发生抵消。

 

证明：

1.2 2×2列联表检验的基本步骤

1．建立检验假设，确定检验水准

：，即两种药物治疗消化道溃疡的愈合率相同

：，即两种药物治疗消化道溃疡的愈合率不同

= 0.05

2．计算统计量

3. 确定P值，做出推断

自由度为=(行数―1)×(列数―1)

按自由度等于1 , 检验水准等于0.05, 查附表得 = 3.84。本例= 4.13，可知<0.05。在=0.05水平上拒绝，两样本频率的差异具有统计学意义。

因为洛赛克的样本愈合率为75.29%，雷尼替丁的愈合率为60.71%，可以认为洛赛克的愈合率比雷尼替丁的愈合率高。

1.3 2×2列联表检验的专用公式

，其中为总体的样本量。

2×2列联表检验的校正公式

校正的原因：首先，卡方（界值）分布其为一个连续型的分布，但是实际数是不连续的，如上面例题中洛赛克组的愈合人数为64人，那么对于这样的实验结果，我们的另外一次实验它的愈合人数如果略多的话，就会是65人，66人，......，70人，实际频数它的变化是不连续的。每一次变化相对于理论数来讲都会是跨度为1的变化，这样的话查边的时候就使得64和（理论频数）之间的差距以及下一次抽样结果65和（理论频数）之间的差距，使得我们在理论连续分布的卡方界值的时候，效果不是很好，于是我们就把64和65中间的这段距离均分，所以0.5是为了让我们解决不连续的资料又要借助连续的分布这样一种条件下，做的一个小小的修正，使得应用效果更加接近卡方分布的曲线下面积的实际情况。

1.4 2×2列联表检验的注意事项

1.校正公式仅用于四格表资料，对多组样本分布，一般不作校正。

2．当四格表资料（总样本量）<40或<1（四个格子当中任意一个格子的理论频数小于1）时，校正值也不恰当，这时可以用Fisher确切概率法检验，见本章第四节。

3．两组疗效对比的必要前提之一，是两组患者“病情相似”，这一点非常重要（即要排除其他干扰因素），只有在两组对象其他方面“同质”的前提下才能比较两个频率，才能进行列联表的检验。

二、多个独立样本R×C列联表资料的检验

2.1 频率的比较

2.1.1 多样本之间的比较

 表示行，表示列，表示对应的列合计，表示对应的行合计。

注意：图中 ，自由度，，32.74远大于5.99，则，三个药品疗效的差异具有统计学意义。

2.1.2 多样本之间的两两比较

 注意：其中，自由度，反查界值表，，如果三者同时对比的时候取得，则需要校正，，不拒绝原假设，AB药品疗效的差异不具有统计学意义。

2.2 独立样本频率的比较

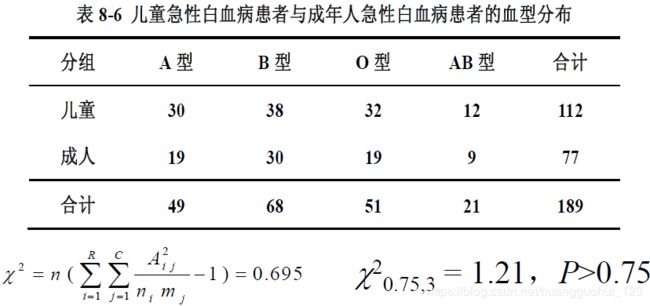
注意：其中，自由度，反查界值表，，，不拒绝原假设，两类患者的血型差异不具有统计学意义，可认为两类型患者的血型来自于同一个分布总体。

2.3 R×C列联表检验注意事项 

R×C列联表检验要求理论频数不宜太小，不宜有1/5以上格子的理论频数小于5，也不宜有一个理论频数小于1，否则有可能产生
偏性。如果出现理论频数不满足此要求，可考虑选择如下方法处理：
(1) 增加样本含量；
(2) 结合专业知识将该格所在行或列与别的行或列合并（例如将上面的A、B、O、AB变成A、B、其他）；
(3) Fisher确切概率法，借助软件实现。

三、配对设计资料的检验

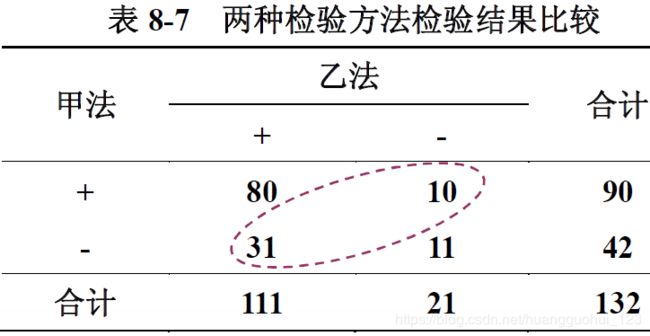
配对设计资料：如下图132个资料都是确诊为阳性的个体，接下来用甲法和乙法来检验两个方法成功检测出的比例。来测试两个方法检验的成功率，是否有高低之分。

甲法的成功率：90/132

乙法的成功率：111/132

两者阳性率的对比可以简化为分子90和111的对比，进一步转化为10和31之间的对比，即前面介绍的四格表资料的b格子和c格子之间的对比。

我们对两种方法成功率的检验可以转化为检测b格子和c格子中的频数是否来自于同一总体，如果b和c被认为来自于同一总体，那么最合理的数值水平大小应该是，因为从这样的总体里最合理的可以得到当前的抽样结局，因为b和c都距离距离相等，如果要回答两种方法成功率是否相等，即回答b和c水平是否能够代表这个总体的水平。

于是，我们先假设b和c来自这个总体，当成立的情况下，理论上b和c应该距离不远,于是我们分别计算b、c和的不吻合度。

1.1 基本思想

计算公式 

计算公式的校正(n=b+c<40)

 1.2 值的计算

此命题中b+c>40，则使用普通公式即可。

注意：按自由度等于1 , 检验水准等于0.05, 查附表得 = 3.84。本例= 10.76，可知<0.05。在=0.05水平上拒绝，两检验方法结果的差异具有统计学意义，且乙法的成功检出率（111/132）大于甲法的成功检出率（90/132）。 

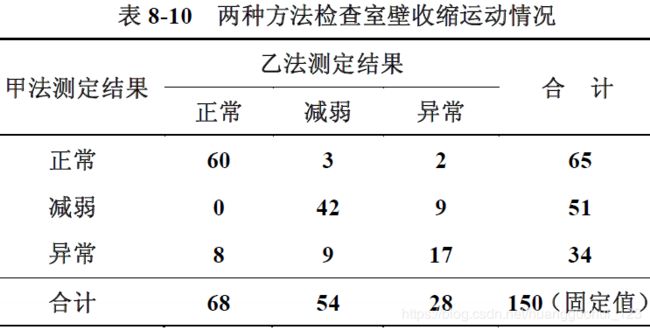
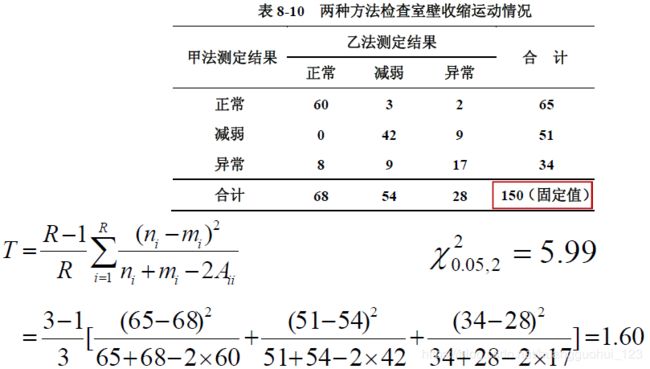
 1.3 配对R×R列联表资料的检验

注意：1、其中R 表示标签类别数。

           2、按自由度等于2 , 检验水准等于0.05, 查附表得 = 5.99。本例= 1.60<5.99，可知>0.05。在=0.05水平上不拒绝，两检验方法结果的差异不具有统计学意义。

           3、配对设计的样本必须是150的样本，必须是总体样本抽取出来的一份随机样本，然后在进行甲乙法的检验，以此相对立的，例如，抽取了甲法“正常”的65人进行乙法的测定，然后抽取了甲法“减弱”的51人进行乙法的测定，有抽取了甲法“异常”的34人进行乙法的测定，这样的检验方法不是配对设计的研究，我们要求的是随机抽取150个样本，分别用甲法乙法进行测定。

 四、列联表资料的确切概率法

注意：

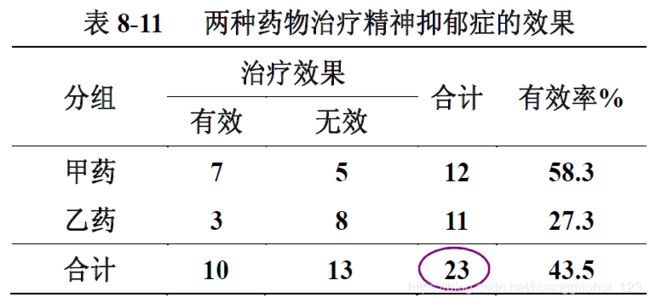
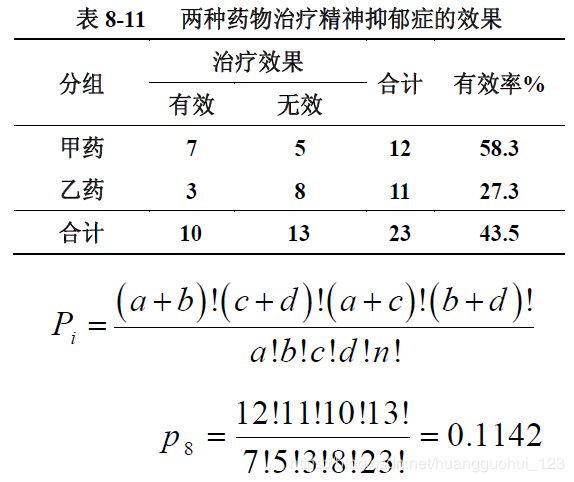
1、n=23<40，样本量太小，用卡方检验或者校正的卡方检验效果不是很好，因为样本量太小，利用连续型卡方来近似检验效果较差。

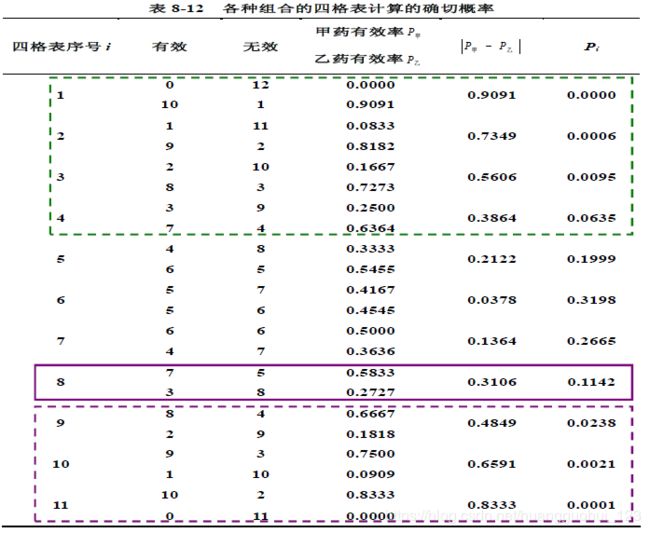
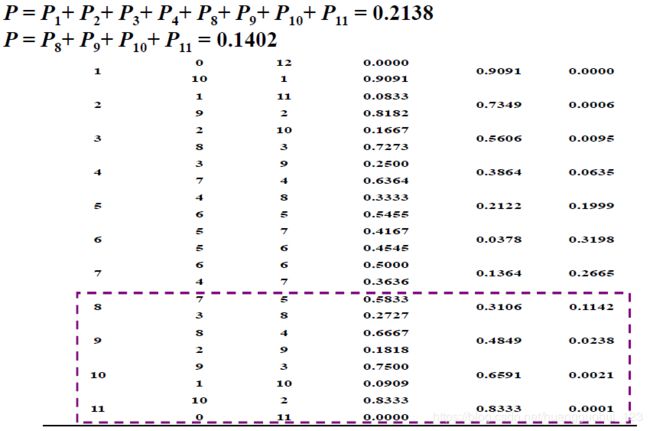
2、行合计和列合计分别为10、13、12、11，最小值为10，即在满足行合计和列合计成立的条件下，可以组合的四个表资料共有11种情况，如下表所示。

成立时所有可能结局有哪些？可能结局有11种。

本研究的“更极端状况”是哪些？即在 成立的情况下，当前结局及更极端状况有1/2/3/4/8/9/10/11这几种情况。

注意： ，表示双侧概率，即当前结局（发生的概率为）和更极端状况（比当前状况的有效率差值更大的情况发生的概率）的概率之和，表示单侧概率，双侧检验和单侧检验均>=0.05，即成立，不认为两种药品的疗效具有统计学意义。

 五、 检验用于拟合优度检验

判断一个定量变量是否服从正态分布，是我们进行参数检验？还是非参数检验？的前提条件。

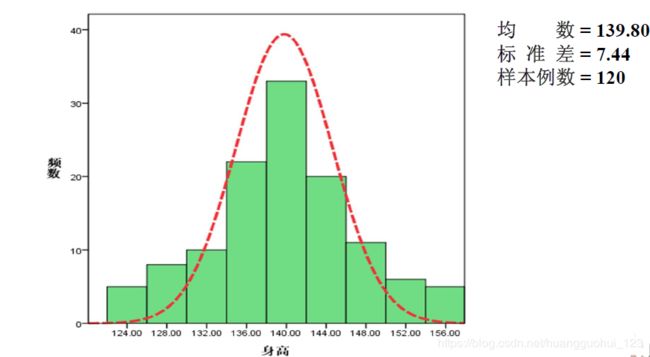
例：随机抽取了某地12岁男孩120名，测其身高如下：

试检验当地12岁男孩的身高是否服从正态分布？ 

注意：

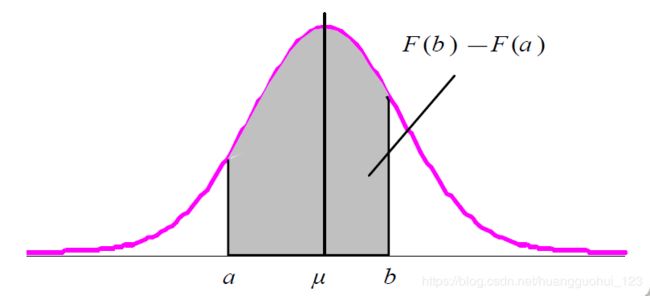
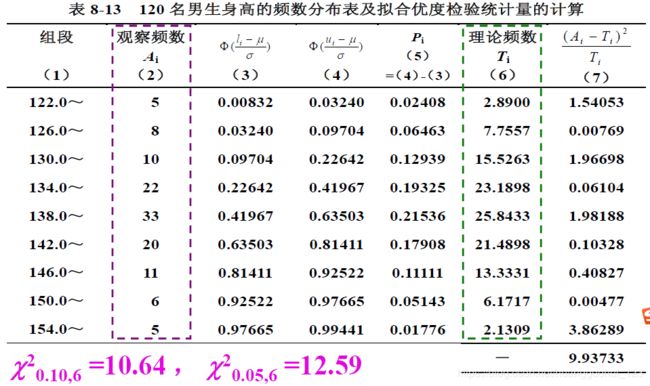
1、（3）表示组段的下边界进行Z转换之后的概率分布面积，（4）表示组段的上边界进行Z转换之后的概率分布面积，（4）-（3）即为组段的下边界和上边界的曲线下面积。[（4）-（3）]*N（N表示样本量，此处为120）即为各组段的理论频数（6）。求出每一个组段的不吻合度，并累加，即得到卡方。

2、自由度=组段数目-3（-1-1表示参数的数目（均值和标准差），-1表示总的样本量的限制），所以此题中的自由度为9-3=6。

3、根据自由度6，查卡方界值表，，，均大于9.93，则认为差异无统计学意义，即认为实际资料是按照理论假定的正太分布模式分布着的。

 拟合优度检验注意事项

1、每组中的理论频数不小于5，否则需要合并组段

2、 合并后样本含量仍不大，则应进行连续性校正（注意，对不符合样本含量条件的组段进行校正即可，其余组段无需校正）