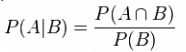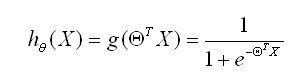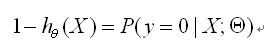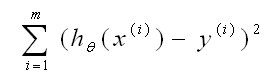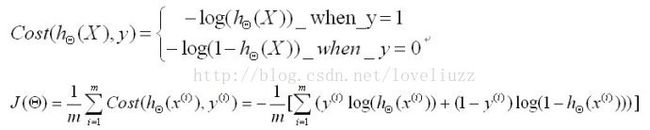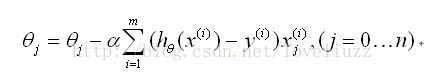机器学习——非线性回归（ Logistic Regression）及应用
1、概率
（1）定义：概率（Probability）：对一件事情发生的可能性的衡量。
（2）取值范围：0<=P<=1
（3）计算方法：根据个人置信、根据历史数据、根据模拟数据
（4）条件概率：在事件B已经发生的情况下，事件A发生的概率等于事件A、B同时发生的概率除以B事件发生的概率。
2、逻辑回归（Logistic Regression）
（1）例子：
h（x）>0.5（恶性），Malignant=1
h（x）>0.2，Malignant=1
比较两种情况，新的数值加入时需要不断调整阈值，说明用线性的方法进行回归不太合理。
（2）基本模型
测试数据为：X(x0,x1,...,xn)
要学习的参数为：
向量表示：
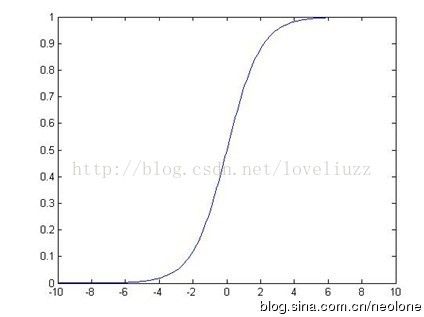
处理二值的数据（自变量x取任意值，因变量y只能取0或1），引入sigmoid函数将曲线平滑化：
，经过点（0,0.5）
预测函数：
用概率表示：
正例（y=1）：
，对于给定的一组数据自变量和一组参数，y=1的概率。
反例（y=0）：
（3）cost函数
线性回归：
使其最小
，在线性回归中，找到合适的
、
使上式最小。
逻辑回归（Logistic Regression）：
cost函数：
目标：找到合适的、使上式的值最小，求导数使其为0，即可求得。
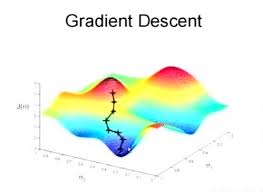
（4）解法：梯度下降（gredient descent）
梯度下降法是用负梯度方向为搜索方向的，最速下降法越接近目标值，步长越小，前进越慢。可以用于求解非线性方程组。
梯度下降法的计算过程就是沿梯度下降的方向求解极小值。
更新法则：
，i是指不同的实例。
3、梯度下降算法实现代码
#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author:ZhengzhengLiu
import numpy as np
import random
#梯度下降算法
def gradientDescent(x,y,theta,alpha,m,numIteration): #输入实例、分类标签、要学习的参数、学习率、实例个数、迭代次数
xTrans = x.transpose() #矩阵的转置
for i in range(0,numIteration):
hypothsis = np.dot(x,theta)
loss = hypothsis - y
cost = np.sum(loss**2)/(2*m)
print("Iteration %d / Cost:%f" %(i,cost))
gradient = np.dot(xTrans,loss)/m
theta = theta - alpha * gradient #更新法则
return theta
#创建数据，用作测试
def genData(numPoints,bais,variance): #实例（行数）、偏向、方差
x = np.zeros(shape=(numPoints,2)) #初始化numPoints行2列(x1,x2)的全零元素矩阵
y = np.zeros(shape=numPoints) #归类标签
for i in range(0,numPoints):
x[i][0] = 1 #所有行第1列为：1
x[i][1] = i #所有行第2列为：行的数目
y[i] = (i + bais) + random.uniform(0,1)*variance
return x,y
x,y = genData(100,25,10)
print("x:",x)
print("y:",y)
m,n = np.shape(x)
n_y = np.shape(y)
numIteration = 100000
alpha = 0.0005
theta = np.ones(n) #初始化theta
theta = gradientDescent(x,y,theta,alpha,m,numIteration)
print(theta)