概率统计（三）常见分布与假设检验

一、一般随机变量

根据随机变量可能取值的个数分为离散型和连续型两类。

• 离散型随机变量
  对于离散型随机变量，使用概率质量函数（PMF）来描述其分布规律。
  用到PMF的分布：二项分布、泊松分布
• 连续型随机变量
  对于连续型随机变量，使用概率密度函数（PDF）来描述其分布情况。
  用到PDF的分布：均匀分布、正态分布、指数分布
  连续型随机变量的特点在于取任何固定值的概率都为0，因此讨论其在特定值上的概率都是没有意义的，应当讨论其在某一个区间范围内的概率，这就用到了概率密度函数的概念
  假定连续型随机变量X，f(x)为概率密度函数，对于任意实数范围如[a, b]，有
  $$P(X)={\int }_a^{b}f(x)dx,a<=X<=b$$
  对于连续型随机变量，通常还会用到累积分布函数（CDF）来描述其性质，在数学上CDF是PDF的积分形式。
  分布函数F(x)在点x处的函数值表示X落在区间(-∞, x]内的 概率，所以分布函数就是定义域为R的一个普通函数，因此我们可以把概率问题转化为函数问题，从而可以利用普通的函数知识来研究概率问题，增大了概率的研究范围。

二、常见分布

在之前的文章中有介绍过数据的分布：概率统计（一）随机事件与随机变量
这里对之前未做介绍的内容做一个补充

1.离散型分布

（1）二项分布

• 二项分布需要满足以下条件：
  （1）试验次数是固定的
  （2）每次试验都是独立的
  （3）对于每次试验成功的概率都是一样的

（2）泊松分布

• 泊松分布需要满足的条件：
  （1）试验次数n趋向于无穷大
  （2）单次事件发生的概率p趋向于0
  （3）np是一个有限的数值

• 二项分布，泊松分布，正态分布的关系
  当n很大，p很小时，如n >= 100 and np <= 10，二项分布可近似为泊松分布
  当λ很大时，如λ >= 1000时，泊松分布可近似为正态分布
  当n很大时，np和n(1-p)都足够大时，如n >= 100 and np >= 10 and n(1-np) >= 10时，二项分布可近似为正态分布

（3）几何分布

• 定义
  考虑独立重复试验，几何分布描述的是经过k次试验才首次获得成功的概率，假定每次成功率为p，那么
  P{X = n} = (1 - p)^n-1p
• 特性
  它的一个重要性质是无记忆性
• 举例
  举个栗子，求婚101次，求婚成功的概率为0.5，第101次才被接受的概率，则
  P（求婚101次获得成功）=（1-0.5）¹⁰⁰ * 0.5
  几何分布的期望是E(x)=1/p，具体含义为，如果你每次求婚成功的概率为0.5，那么你可以期望自己求婚2次就获得成功

（4）负二项分布

• 定义
  考虑独立重复试验，负二项分布描述的是试验一直进行到成功r次的概率，假定每次成功率为p，那么
  

• 应用
  在实际的生活中，负二项分布可以应用到很多场景。一个人在获得r次满分前，没有获得满分的次数；一台机器在坏掉之前，可以使用的天数等等。

（5）超几何分布

如果样本容量n=1，即从有限总体中只抽取一个个案，且恰好抽到符合要求个案的概率，那么超几何分布可以还原成二项分布。

如果数据总体的容量N无穷大，也就是将有限总体换成无限总体，此时抽中的个案放回与不放回对于总体中符合要求的个案比例都没有影响，超几何分布也可视为二项分布。

在实际应用时，只要数据总体的个案数目是样本容量的10倍以上，即N > 10n，就可用二项分布近似描述超几何分布，通过两种概率质量函数计算得到的概率几乎相同。

2.连续型分布

（1）均匀分布

均匀分布指的是一类在定义域内概率密度函数处处相等的统计分布

（2）正态分布

• 定义
  正态分布只依赖于数据集的两个特征：样本的均值和方差：
  均值——样本所有取值的平均
  方差——该指标衡量了样本总体偏离均值的程度

正态分布的这种统计特性使得问题变得异常简单，任何具有正态分布的变量，都可以进行高精度分预测，大自然中发现的变量，大多近似服从正态分布。
正态分布很容易解释，这是因为正态分布的均值，模和中位数是相等的，且我们只需要用均值和标准差就能解释整个分布。

（3）指数分布

指数分布通常被广泛用在描述一个特定事件发生所需要的事件，在指数分布随机变量的分布中，有着很少的大树值和非常多的小数值。
指数分布是无记忆的，假定在等候事件发生的过程中已经过了一些事件，此时距离下一次事件发生的时间间隔的分布情况和最开始是完全一样的，不会对结果有任何影响。

（4）Γ分布

通常用来描述某个事件总共要发生n次的等待时间的分布。
Gamma分布常用于概率统计模型,它在水文学和气象学、可靠性和生存分析等领域都有广泛的应用。因此,对Gamma分布特别是Gamma分布的参数估计展开研究有着重要意义。
指数分布是伽马分布α = 1的特殊情况

（5）威布尔分布（Weibull）

常用来描述在工程领域中某类具有最弱链对象的寿命。

3.常见分布的均值和方差汇总

离散型分布：

连续型分布：

以及对各个分布做了一个对比汇总：

4.Python代码实战

（1）生成一组符合特定分布的随机数

import numpy as np
#生成大小为1000的符合b(10,0.5)二项分布的样本集
s_b = np.random.binomial(n=10,p=0.5,size=1000)
print(s_b)
#生成大小为1000的符合P(1)泊松分布的样本集
s_p = np.random.poisson(lam=1,size=1000)
print(s_p)
#生成大小为1000的符合U(0,1)均匀分布的样本集，注意在此方法中边界值为左闭右开区间
s_u = np.random.uniform(low=0,high=1,size=1000)
print(s_u)
#生成大小为1000的符合N(0,1)正态分布的样本集，可以用normal函数自定义均值、标准差，也可以直接使用standard_normal函数
s_n1 = np.random.normal(loc=0,scale=1,size=1000)
print(s_n1)
s_n2 = np.random.standard_normal(size=1000)
print(s_n2)
#生成大小为1000的符合E(1/2)指数分布的样本集，注意该方法中的参数为指数分布参数λ的倒数
s_e = np.random.exponential(scale=2,size=1000)
print(s_e)

（2）计算统计分布的PMF和PDF

from scipy import stats
import numpy as np
#计算二项分布B(10,0.5)的PMF
x_b = range(11)
p_b = stats.binom.pmf(x_b,n=10,p=0.5)
print(p_b)
#计算泊松分布P(1)的PMF
x_p = range(11)
p_p = stats.poisson.pmf(x_p,mu=1)
#计算均匀分布U(0,1)的PDF
x_u = np.linspace(0,1,100)
p_u = stats.uniform.pdf(x_u,loc=0,scale=1)
#计算正态分布N(0,1)的PDF
x_n = np.linspace(-3,3,1000)
p_n = stats.norm.pdf(x_n,loc=0,scale=1)
#计算指数分布E(1)的PDF
x_e = np.linspace(0,10,1000)
p_e = stats.expon.pdf(x_e,loc=0,scale=1)
#计算统计分布的CDF
x = np.linspace(-3,3,1000)
p = stats.norm.cdf(x,loc=0,scale=1)

（3）统计分布可视化

• 二项分布
  比较n=10,p=0.5的二项分布的真实概率质量和10000次随机抽样的结果

from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns

x = range(11) #二项分布成功的次数（x轴）
t = stats.binom.rvs(10,0.5,size=10000) #B(10,0.5)随机抽样10000次
p = stats.binom.pmf(x,10,0.5) #B(10,0.5)真是概率质量

fig,ax = plt.subplots(1,1)
sns.distplot(t,bins=10,hist_kws={'density':True},kde=False,label='Displot from 10000 samples')
sns.scatterplot(x,p,color='purple')
sns.lineplot(x,p,color='purple',label='True mass density')
plt.title('Binomial distribution')
plt.legend(bbox_to_anchor=(1.05,1))
plt.show()

查看输出结果：

• 泊松分布
  比较λ=2的泊松分布的真实概率质量和10000次随机抽样的结果

from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns

x = range(11)
t = stats.poisson.rvs(2,size=10000)
p = stats.poisson.pmf(x,2)

fig,ax = plt.subplots(1,1)
sns.distplot(t,bins=10,hist_kws={'density':True},kde=False,label='Distplot from 10000 samples')
sns.scatterplot(x,p,color='purple')
sns.lineplot(x,p,color='purple',label='True mass density')
plt.title('Poisson distribution')
plt.legend(bbox_to_anchor=(1.05,1))
plt.show()

查看输出结果：

比较不同参数λ对应的概率质量函数，可以验证随着参数增大，泊松分布开始逐渐变得对称，分布也越来越均匀，趋近于正态分布

from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns

x = range(50)
fig,ax = plt.subplots()
for lam in [1,2,5,10,20]:
    p = stats.poisson.pmf(x,lam)
    sns.lineplot(x,p,label='lamda='+str(lam))
plt.title('Poisson distribution')
plt.legend()
plt.show()

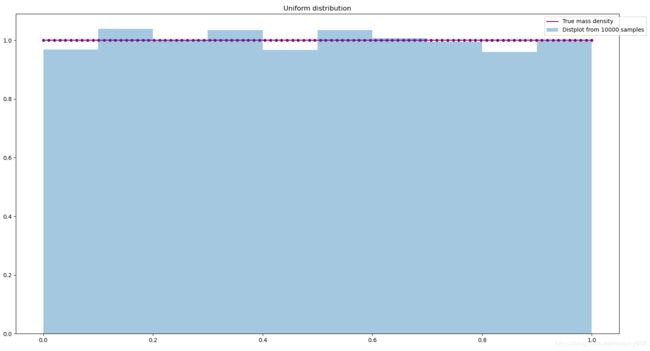
• 均匀分布
  比较U(0,1)的均匀分布的真实概率密度和10000次随机抽样的结果

from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

x = np.linspace(0,1,100)
t = stats.uniform.rvs(0,1,size=10000)
p = stats.uniform.pdf(x,0,1)

fig,ax = plt.subplots(1,1)
sns.distplot(t,bins=10,hist_kws={'density':True},kde=False,label='Distplot from 10000 samples')
sns.scatterplot(x,p,color='purple')
sns.lineplot(x,p,color='purple',label='True mass density')
plt.title('Uniform distribution')
plt.legend(bbox_to_anchor=(1.05,1))
plt.show()

• 正态分布
  比较N(0,1)的正态分布的真实概率密度和10000次随机抽样的结果

from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

x = np.linspace(-3,3,100)
t = stats.norm.rvs(0,1,size=10000)
p = stats.norm.pdf(x,0,1)

fig,ax = plt.subplots(1,1)
sns.distplot(t,bins=10,hist_kws={'density':True},kde=False,label='Distplot from 10000 samples')
sns.scatterplot(x,p,color='purple')
sns.lineplot(x,p,color='purple',label='True mass density')
plt.title('Normal distribution')
plt.legend(bbox_to_anchor=(1.05,1))
plt.show()

比较不同均值和标准差组合的正态分布的概率密度函数

from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

x = np.linspace(-6,6,100)
p = stats.norm.pdf(x,0,1)
fig,ax = plt.subplots()
for mean,std in [(0,1),(0,2),(3,1)]:
    p = stats.norm.pdf(x,mean,std)
    sns.lineplot(x,p,label='Mean:'+str(mean)+',std:'+str(std))
plt.title('Normal distribution')
plt.legend()
plt.show()

• 指数分布
  比较E(1)的指数分布的真实概率密度和10000次随机抽样的结果

from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

x = np.linspace(0,1,100)
t = stats.expon.rvs(0,1,size=10000)
p = stats.expon.pdf(x,0,1)

fig,ax = plt.subplots(1,1)
sns.distplot(t,bins=10,hist_kws={'density':True},kde=False,label='Distplot from 10000 samples')
sns.scatterplot(x,p,color='purple')
sns.lineplot(x,p,color='purple',label='True mass density')
plt.title('Exponential distribution')
plt.legend(bbox_to_anchor=(1,1))
plt.show()

比较不同参数的指数分布的概率密度函数

from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

x = np.linspace(0,10,100)
fig,ax = plt.subplots()
for scale in [0.2,0.5,1,2,5]:
    p = stats.norm.pdf(x,scale=scale)
    sns.lineplot(x,p,label='lamda:'+str(1/scale))
plt.title('Exponential distribution')
plt.legend()
plt.show()

三、假设检验

1.基本概念

• 假设检验
  （1）定义
  假设检验是统计推断中的一类重要问题，在总体分布函数完全未知，或只知其形式，不知其参数的情况，事先对总体参数或分布形式作出某种假设，然后利用样本信息来判断原假设是否成立，采用逻辑上的反证法，依据统计上的小概率原理，这类问题被称为假设检验。
  （2）核心思想
  假设检验的核心思想是小概率反证法，在假设的前提下，估算某事件发生的可能性，如果该事件是小概率事件，在一次研究中本来是不可能发生的，现在发生了，这时候就可以推翻之前的假设，接受备择假设。如果该事件不是小概率事件，我们就找不到理由来推翻之前的假设，实际中可引申为接受所做的原假设。
• H₀假设
  也称零假设或原假设，是在假设检验中被用来检验的假设，一般是我们希望能被推翻的假设。通常会将原假设描述成变量之间不存在某种差异，或不存在某种关联。
• H₁假设
  也称备择假设。它与零假设相互对立，拒绝零假设就自然接受备择假设。
• 小概率事件
  一般指概率小于等于0.05的事件，并且认定其在一次试验中基本上不会发生。
• 反证法
  这是假设检验的根本逻辑，前文我们提出因为不好直接得到总体的真实值，于是先提出一个假设，如果我们获得的样本信息不支持该假设，就拒绝该假设。
• 检验水准
  人为规定的一个数字，表示拒绝实际上成立的的最大允许概率，实际工作中常取0.05，用α表示。
• 检验统计量
  大家熟悉的z检验、t检验，这里的z和t就是检验统计量的一种，它实际上是把估计值与我们的假设值之间的差异进行的标准化，方便我们来评估总体参数之间的差异是否大，大家完全可以把它理解成一种“差”的概念，其值越大，代表差异越大。
• p值
  当原假设为真时所得到的样本观察结果或更极端结果出现的概率。
  如果P值很小，说明原假设情况的发生的概率很小，而如果出现了，根据小概率原理，我们就有理由拒绝原假设，P值越小，我们拒绝原假设的理由越充分。
  
• 单尾检验
  拒绝域落在可能的数据集的一侧
• 双尾检验
  拒绝域落在可能的数据集的两侧
  使用单尾检验还是双尾检验取决于备择假设的形式：
  
  
  举例理解假设检验：
  假设有一袋豆子，袋子里有红豆，也有黑豆，想知道红豆和黑豆是不是一样多。于是从袋子里拿了一把豆子，看看这把红豆多还是黑豆多。用这把豆子作为样本，去推断这袋豆子。既然是用样本推断总体，就有抽样误差的可能性。不管袋子里红豆多还是黑豆多，这一把不一定能真实反映这袋豆子，那怎么办呢？这就要用到假设检验了。
  原假设：袋子里红豆和黑豆是一样多的，如果观察到红豆黑豆不一样多完全是由抽样造成的。
  备择假设：袋子里红豆和黑豆的确不一样多。
  ①假定袋子里有100个豆子，50个红豆，50个黑豆。拿的这把豆子有3个红豆，7个黑豆。在原假设成立的前提下，也就是说红豆黑豆一样多的基础上，能拿到3个红豆、7个黑豆的概率为：
  C(50,3) * C(50,7) / C(100,10) = 0.113
  说明在红豆和黑豆一样多的假设下，拿到3个红豆7个黑豆的可能性为0.11，是很常见的，说明所做的假设是可以成立的，还没有理由能拒绝无效假设。
  ②假定袋子里有100个豆子，50个红豆，50个黑豆。拿的这把豆子有1个红豆，9个黑豆。在原假设成立的前提下，能拿到1个红豆、9个黑豆的概率为：
  C(50,1) * C(50,9) / C(100,10) = 0.007
  在红豆和黑豆一样多的假设下，拿到1个红豆9个黑豆的可能性为0.007＜0.05，为小概率事件，在一次研究中是不应该发生的，而现在发生了，可能是所做的假设有问题，有理由拒绝原假设。

2.基本步骤

通过如下案例来展现假设检验的基本过程：
随机抽取某校500名男生和500名女生，调查去年“双十一”的花费，发现女生平均花费为771元（标准差为1801），而男生平均花费是478元（标准差为400），能否推断该校女生比男生平均花费多？
（1）建立检验假设，确定检验水准
H₀：该校男生和女生双十一花费相同（μ_d = 0）
H₁：该校女生去年双十一花费高于男生（μ_d> 0）
μ_d = μ_女 - μ_男
（2）检验统计量的选择与计算
检验统计量是对估计值与假设检验之间的差异进行标准化转换，从而评估总体参数之间是否存在差异，总体标准差已知或样本容量大于30，比较两个样本的均值是否有显著性的差异，检验公式如下

（3）计算P值，做出统计推断
z = (771 - 478) / √(1801² / 500 + 400² / 500) = 3.55
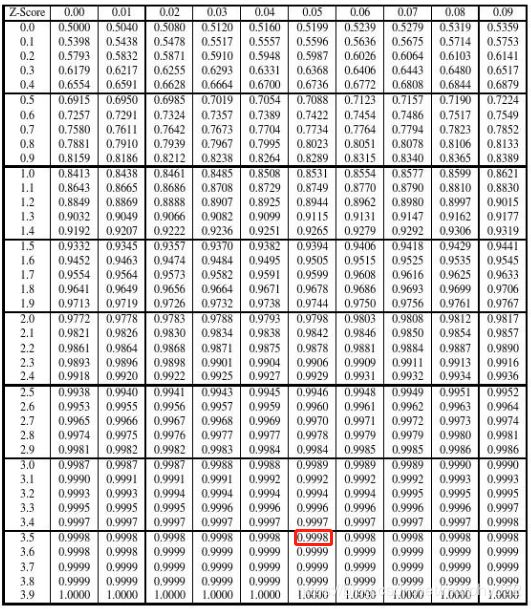
根据z分布图表查询可得，p = 0.0002 < 0.05，按照α = 0.05水准，拒绝H₀，差异具有统计学意义，可以认为该校女生平均网购花费高于男生。
z分布图表查询：

3.选择统计量

检验统计量：为了进行假设检验，从总体中随机抽取样本，计算相关统计量。这个统计量随检验类型的不同而不同，但是它在零假设下的分布必须是已知的(或假设的)。
（1）p：检验的p值是零假设下，得到检验统计量或比样本值更极端的值的概率。那么自然，这个p越小，就代表零假设成立的概率越小。因此实验中，我们希望p越小越好。
（2）α：显著性水平α是检验的一个阈值，α的数值必须在假设检验前确定好。一个典型的α的值是0.05。此时比较p和α。
a.如果一个检验的p值小于α,检验拒绝零假设。
b.如果p值大于α,没有足够的证据拒绝零假设。注意，拒绝原假设的证据不足并不代表接受原假设。

（1）T检验

T检验是通过比较不同数据的均值，研究两组数据之间是否存在显著差异。

• 适用条件
  （1）T检验是用于小样本（样本容量小于30）的两个平均值差异程度的检验方法。
  （2）T检验的适用条件为样本分布符合正态分布。
• 应用条件
  （1）当样本例数较小时，要求样本取自正态总体
  （2）做两样本均数比较时，还要求两样本的总体方差相等。
• T检验的用途：
  （1）样本均数与群体均数的比较
  （2）两样本均数的比较
• T检验的三种形式
  

①单样本T检验

用于检验样本的分布期望是否等于某个值，原假设：μ=μ₀

• 统计量计算：

• 自由度：v= n - 1
• ​ 适用条件：
  （1）已知一个总体均数μ₀
  （2）可得到一个样本均数及该样本标准差S，样本数n
  （3）样本来自正态或近似正态总体
• 案例
  

②配对样本T检验

配对样本t检验针对配对的两组样本。假设两组样本之间的差值服从正态分布。如果该正态分布的期望为零，则说明这两组样本不存在显著差异。原假设：μ_d = 0

• 统计量计算
  
• 举例
  

③独立样本T检验

该检验用于检验两组非相关样本均值之间的差异性，从而判断两样本所代表的总体均值是否有差异

• 统计量计算：

• 举例
  

（2）Z检验

Z检验是一般用于大样本(即样本容量大于30)平均值差异性检验的方法。当已知标准差时，验证一组数的均值是否与某一期望值相等时，用Z检验。

• 检验一个样本的平均值与一个已知总体的平均值是否存在显著差异，Z值计算公式如下：

• 检验来自两个不同总体的两组样本平均数的差异性，从而判断它们各自代表的总体的差异是否显著，Z值计算公式：
  
  其中：
  X₁：样本1的均值
  S₂：样本2的均值
  S₁：样本1的标准差
  S₂：样本2的标准差
  n₁：样本1的样本容量
  n₂：样本2的样本容量
• Z检验的步骤

①确立原假设H₀：两个平均数之间没有差异
②根据z值计算公式计算出z值
③根据显著性关系与z值做出判断

• 举例
  根据过去大量资料，某厂生产的灯泡使用寿命符合正态分布N~(1020,100²) ，从最近生产的一批灯泡中随机抽取100只，测得样本平均值为1080，在0.05的显著性水平下判断这批产品的使用使用寿命是否显著提高。
  H₀：样本均值与总体均值无显著差异
  根据公式计算Z值为
  
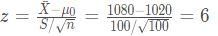
  在0.05的显著性水平下，由于6 > 1.96,因此拒绝原假设，认为样本均值与总体均值存在显著差异。

（3）F检验

F检验法是英国统计学家Fisher提出的，主要通过比较两组数据的方差S²，以确定他们的精密度是否有显著性差异。

• 方差齐性检验
  （1）应用背景
  从两研究总体中随机抽取样本，要对这两个样本进行比较的时候，要首先判断两总体方差是否相同，即方差齐性，若两总体方差相等，则直接使用t检验，若不等，可采用t^’检验或变量变换或秩和检验等方法，其中要判断两总体方差是否相等，就可以使用F检验。
  （2）样本要求
  样本来自两个独立的、服从正态分布的总体。
  （3）公式推导
  记两独立总体为：X₁ ~ N(μ₁, δ₁²)，X₂ ~ N(μ₂, δ₂²)
  从两总体中抽取的样本为：X_1i(i = 1, 2, … , n₁)，X_2j(j = 1, 2, … , n₂)
  定义样本均值和样本方差：
  
  ①方差齐性双侧检验的原假设和备择假设：
  H₀：δ₁² = δ₂²，即两总体方差相等
  H₁：δ₁² ！= δ₂²，即两总体方差不相等
  由F分布的构造定义：(s₁² / δ₁²) / (s₂² / δ₂²) ~ F(n₁ - 1, n₂ - 1)
  其中n₁ - 1、n₂ - 1分别为分子自由度和分母自由度
  在H₀成立的条件下，δ₁² = δ₂²，有 s₁² / s₂² ~ F(n₁ - 1, n₂ - 1)
  若F₁ = s₁² / s₂² > F_α/2 (n₁-1, n₂-1)，此时拒绝原假设，认为方差不齐
  ②对于单侧检验：
  H₀：δ₁² < δ₂²
  H₁：δ₁² >= δ₂²
  若F₂ = s₁² / s₂² > F_α (n₁-1, n₂-1)，此时拒绝原假设，认为方差不齐
  ③对于单侧检验：
  H₀：δ₂² < δ₁²
  H₁：δ₂² >= δ₁²
  若F₃ = s₁² / s₂² < F_1-α (n₁-1, n₂-1)，此时拒绝原假设，认为方差不齐
• 方差分析（单因素）
  所有的方差分析研究的都是因子的不同水平是否有差异，这个差异就是看同一因子的各个水平下的指标的均值差异是否显著，例如我们要研究一个因素对于一个指标的影响，试图比较这个因素内各个取值水平对于这个指标的影响是否相同。
  （1）F统计量
  $$F=\frac{SSA/df1}{SSE/df2}$$
  其中：SSA是各个水平之间的偏差平方和，也可以说成是组间偏差平方和
  SSE是各个水平内部的偏差平方和，也可以说成是组内偏差平方和
  df1、df2分别是它们的自由度（由于SSA和SSE都只是偏差的平方和，若这两个计算的数量不一样，譬如SSA计算了十个偏差的平方和，而SSE只计算了五个，那么SSA/SSE就会因为组间、组内这些数量无法度量，所以除以自由度得出方差，保证了这两个偏差的平方和在平均意义下是可比的）
  组间方差（组间变异）：SSA / df1，又可以称为由因素自身产生的变异
  组内方差（组内变异）：SSE / df2，又可以称为由误差产生的变异，又称为均方误差（MSE）
  MSA = SSA / (r - 1)，MSE = SSE / (n - r)
  若F = MSA / MSE > F_α(r - 1, n - r)，则拒绝原假设

（4）卡方检验

卡方检验是以χ2分布为基础的一种常用假设检验方法，统计样本的实际观测值与理论推断值之间的偏离程度，主要在分类数据资料统计推断中应用，如两个或多个率/构成比之间的比较以及分类资料的相关分析等。

• 公式
  $$\chi 2=\sum \frac{(A-T{)}^2}{T}$$
  其中：A是实际值，T为理论值
• 步骤
  （1）建立无效假设H₀：观察频数与期望频数没有差别；
  （2）在假设H₀成立基础上，计算出χ2值来表征观察值与理论值之间的偏离程度；
  （3）根据p值（多设定为0.05）及自由度，根据χ2分布查出拒绝H₀假设的临界值；
  （4）若计算得χ2>临界值，即H₀成立的概率＜5%，表示在95%置信水平下，观察值与理论值之间有显著差异；反之，则说明两者无差异。
• 要注意的是，卡方检验受样本量的影响很大，同样两个变量，不同的样本量，可能得出不同的结论。解决这个问题的办法是对卡方值进行修正，最常用的是列联系数。对较大样本，当卡方检验的的结果显著，并且列联系数也显著时，才可拒绝原假设；当卡方检验的结果显著，列联系数不显著时，不能轻易下结论。
  
• 应用场景
  （1）检验某个连续变量的分布是否与某种理论分布相一致。如是否符合正态分布、是否服从均匀分布、是否服从Poisson分布等。
  （2）检验某个分类变量各类的出现概率是否等于指定概率。如在36选7的彩票抽奖中，每个数字出现的概率是否各为1/36；掷硬币时，正反两面出现的概率是否均为0.5。
  （3）检验某两个分类变量是否相互独立。如吸烟(二分类变量：是、否)是否与呼吸道疾病(二分类变量：是、否)有关；产品原料种类(多分类变量)是否与产品合格(二分类变量)有关。
  （4）检验控制某种或某几种分类因素的作用以后，另两个分类变量是否相互独立。如在上例中，控制性别、年龄因素影响以后，吸烟是否和呼吸道疾病有关；控制产品加工工艺的影响后，产品原料类别是否与产品合格有关。
  （5）检验某两种方法的结果是否一致。如采用两种诊断方法对同一批人进行诊断，其诊断结果是否一致；采用两种方法对客户进行价值类别预测，预测结果是否一致。
  有关卡方检验的更详细信息请查看：卡方检验

（5）几种常用检验方法的对比

4.两类错误

当我们进行假设检验的过程中，错误是无法避免的，根据定义，错误分为两类：

• 一类错误：拒绝真的原假设
  一类错误可以通过α值来控制，在假设检验中选择的α对一类错误有着直接的影响。
  以95%的置信水平为例，α = 0.05，这意味着我们拒绝一个真的原假设的可能性是5%，即每做20次假设检验会有一次犯一类错误的事件发生。
• 二类错误：接受错误的原假设
  二类错误通常是由小样本或高样本方差导致的，二类错误的概率可以用β来表示。
  对于二类错误，可以从功效的角度来估计，首先进行功效分析计算出功效值1 - β，进而得到二类错误的估计值β。

一般来说这两类错误是无法同时降低的，在降低犯一类错误的前提下会增加犯二类错误的可能性，在实际案例中如何平衡这两类错误取决于我们更能接受一类错误还是二类错误。

参考资料：
数据分析必备统计学（二）：假设检验
对假设检验的再一次全面剖析
统计学——几种常见的假设检验
一文详解F检验