AtCoder Beginner Contest 131题解

AtCoder Beginner Contest 131

比赛链接

前言

经过100天毒瘤的中考备考后，我终于打了三个月以来的第一场比赛。

似乎ABC加了难度。。。

A.Security

题目大意

给定一个四位数，若其中有相邻数位的数字是相同的，则输出Bad,否则输出Good

参考代码

题目太水，直接上代码。

#include
#include
using namespace std;

int N;

int main() {
	#ifdef LOACL
	freopen("in.txt","r",stdin);
	freopen("out.txt","w",stdout);
	#endif
	scanf("%d",&N);
	if(N%10==N/10%10||N/10%10==N/100%10||N/100%10==N/1000%10)
		puts("Bad");
	else puts("Good");
	return 0;
}

B.Bite Eating

题目大意

给定$N$个数，要求去掉一个数，使得剩余$N-1$个数的和尽可能接近原来$N$个数的和。（注意会出现负数）

参考代码

仔细分析一下就可以发现其实只要把绝对值最小的去掉就行了。

#include
#include
using namespace std;

int N,L;

int abs(int x) {
	if(x<0)return -x;
	return x;
}

bool cmp(int lhs,int rhs) {
	return abs(lhs)<abs(rhs);
}

int main() {
	#ifdef LOACL
	freopen("in.txt","r",stdin);
	freopen("out.txt","w",stdout);
	#endif
	scanf("%d %d",&N,&L);
	int a[200+5];
	for(int i=1;i<=N;i++)
		a[i]=L+i-1;
	sort(a+1,a+N+1,cmp);
	int sum=0;
	for(int i=2;i<=N;i++)
		sum+=a[i];
	printf("%d\n",sum);
	return 0;
}

C.Anti-Division

题目大意

给定四个数$A,B,C,D(1\le A,B\le 10^{18})$，求出区间$[A,B]$之间不能被$C,D$整除的数的个数。

分析

我们将区间里的数分为四类：

1. 不能被$C$或$D$整除的数；
2. 能被$C$整除的数；
3. 能被$D$整除的数；
4. 既能被$C$整除，又能被$D$整除的数。

其中第2,3,4种数的个数是十分好求出的。

我们考虑容斥原理，如图所示：
要求出1中的数，只需求出2,3,4中的数，再容斥一下就可以了。

参考代码

#include
#include
using namespace std;

typedef long long ll;

ll A,B;
ll C,D;

int GCD(int a,int b) {
	if(b==0)return a;
	return GCD(b,a%b);
}

int main() {
	#ifdef LOACL
	freopen("in.txt","r",stdin);
	freopen("out.txt","w",stdout);
	#endif
	scanf("%lld %lld %lld %lld",&A,&B,&C,&D);
	ll t1=B/C-(A-1)/C;
	ll t2=B/D-(A-1)/D;
	ll g=C*D/GCD(C,D);
	ll t3=B/g-(A-1)/g;
	printf("%lld",(B-A+1)-t1-t2+t3);
	return 0;
}

D.Megalomania

题目大意

有$N$个工作，第$i$个工作必须耗费$A_i$单位时间，必须在$B_i$时间之前完成。同一时间不能做两项工作，问能否将这些工作都完成。

分析

其实就是一道简化版的建筑抢修。。。

用优先队列贪心一下就是了。。。

参考代码

#include
#include
#include
using namespace std;

const int Maxn=2e5;

int N;
struct Node {
	int t1,t2;
	bool operator < (const Node &rhs) const {return t2<rhs.t2;}
}A[2*Maxn+5];
priority_queue<int> q;
int main() {
	#ifdef LOACL
	freopen("in.txt","r",stdin);
	freopen("out.txt","w",stdout);
	#endif
	scanf("%d",&N);
	for(int i=1;i<=N;i++)
		scanf("%d %d",&A[i].t1,&A[i].t2);
	sort(A+1,A+N+1);
	int t=0,tot=0;
	for(int i=1;i<=N;i++) {
		if(t+A[i].t1<=A[i].t2) {
			tot++;
			t+=A[i].t1;
			q.push(A[i].t1);
		} else {
			if(q.empty())continue;
			int maxx=q.top();
			if(A[i].t1<maxx){
                q.pop();
                q.push(A[i].t1);
                t=t-maxx+A[i].t1;
            }
		}
	}
	if(tot==N)puts("Yes");
	else puts("No");
	return 0;
}

E.Friendships

最后两分钟交的，真刺激。。。

题目大意

给定$N$个点，要求构造一个简单图，使得其中恰好有$K$个点对$(u,v)(u<v)$的距离恰等于$2$。

分析

分析一下就会发现：“菊花图”所产生的点对数量是最多的，如下图所示：

当我们连上任意两个“花瓣”后，点对的数量就减少了一个。

所以我们只需求出$\frac{(N-1)(N-2)}{2}-K$后连上这么多的边就是了。

参考代码

#include
#include
#include
using namespace std;

const int Maxn=100;

int N,K;

vector<int> e[Maxn+5];

vector<int> ans1,ans2;

int main() {
	#ifdef LOACL
	freopen("in.txt","r",stdin);
	freopen("out.txt","w",stdout);
	#endif
	scanf("%d %d",&N,&K);
	if((N-1)*(N-2)/2<K) {
		puts("-1");
		return 0;
	}
	for(int i=2;i<=N;i++) {
		e[i].push_back(1);
		e[1].push_back(i);
	}
	for(int i=2;i<=N;i++)
		ans1.push_back(1),ans2.push_back(i);
	int t=(N-1)*(N-2)/2-K;
	for(int i=2,k=1;i<=N;i++) {
		for(int j=i+1;j<=N;j++) {
			if(k>t)break;
			if(i==j)continue;
			ans1.push_back(i),ans2.push_back(j);
			k++;
		}
		if(k>t)break;
	}
	printf("%d\n",ans1.size());
	for(int i=0;i<ans1.size();i++)
		printf("%d %d\n",ans1[i],ans2[i]);
	return 0;
}

F.Must Be Rectangular!

这题我考试的时候没做出来。。。

三个月不上机果然连ABC都没办法AK了。。。

题目大意

给定$N$个坐标系上的点$(x_i,y_i)$,若有如下图所示的三个点（黑点）就可以构造岀一个新的点（红点）。求可构造的点的最多的个数。

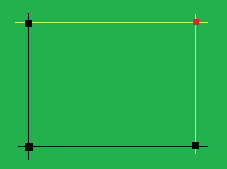
分析

分析一下可以发现，只要我们找出X轴上有多少条竖线，Y轴上有多少条横线，就可以求出总的点数，再特判一下，就可以得到答案。

但是这是一个复杂度为$O(N^2)$的算法。

所以我们可以考虑利用并查集。

我们在读入一个点时，将它的横坐标和纵坐标加到一个集合里面，表示该点可构造岀一个“十字型”。为了方便，我们将纵坐标加上一个常数就可以利用并查集了。

最后只需统计各个坐标轴上点的个数，相乘并减去原有的点即可。

参考代码

#include
#include
#include
using namespace std;

typedef long long ll;
const int O=1e5;

int fa[2*O+5];
ll cnt1[2*O+5],cnt2[2*O+5];

int find(int x) {
	if(fa[x]==x)return x;
	return fa[x]=find(fa[x]);
}

int main() {
	#ifdef LOACL
	freopen("in.txt","r",stdin);
	freopen("out.txt","w",stdout);
	#endif
	for(int i=0;i<=2*O;i++)
		fa[i]=i;
	int N;
	scanf("%d",&N);
	for(int i=1;i<=N;i++) {
		int x,y;
		scanf("%d %d",&x,&y);
		fa[find(x)]=fa[find(y+O)];
	}
	for(int i=1;i<=O;i++)
		cnt1[find(i)]++;
	for(int i=O+1;i<=O*2;i++)
		cnt2[find(i)]++;
	ll ans=0;
	for(int i=1;i<=O*2;i++)
		ans+=cnt1[i]*cnt2[i];
	printf("%lld\n",ans-N);
	return 0;
}