Unity Shader 凹凸映射

预备知识

什么是凹凸映射？

在普通纹理作用下，我们实现了给模型“穿衣服”的效果，实现了真实感渲染的第一步。但是，普通的单张纹理的能力很有限。比如，当我们模拟一个砖墙的材质时，单张纹理在远处看来，效果还算可以；但是，当我们靠近这个材质时，我们发现，原本应该粗糙的砖墙表面，竟然比“磨皮”之后的效果还要平滑，就像是贴了一个壁纸。这是为什么呢？

单张纹理只是调制了材质的漫反射颜色，让它看起来是那么回事。但是我们知道，实际上几乎所有材质的表面都是凹凸不平的。那么，这些凹凸不平的效果又是怎么实现的呢？
当然，为了实现凹凸不平的效果，最简单的思路是在建模的时候将模型建成凹凸不平的表面，抛开精度不谈，这种建模方法势必会导致三角形面片数量成几何增长(类似于迭代细分)；那么换个角度，我们所看到的材质效果，实际上大部分是由着色模型决定的，对于凹凸表面而言，最终效果就是由于表面细小的凹凸片元的法向量不一致导致的。因此，我们只要在光照计算的时候更改模型表面法线，就可以达到凹凸不平的效果。

如何实现凹凸映射？

• 高度纹理(Height Map)
  高度纹理存储了每个位置的相对高度，很直观，但不实用。我们可以通过高度图看到模型表面的凹凸情况，但是对于shader而言，需要额外计算每个位置的法线，效率极低。

• 法线纹理(Noraml Map)
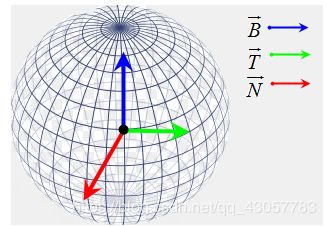
  法线纹理是实现凹凸映射的关键，法线纹理是一张“特殊”的纹理，存储了每个位置切线空间的法向量。每个顶点都有自己的切线空间，这个空间的z轴是顶点法线方向，x轴是顶点切线方向，y轴是z轴与x轴的叉乘结果，称为副切线(Bitangent)或副法线(Binormal)。对于法向量而言，每个分量的范围是[-1,1]；而对于颜色值而言，每个分量为[0,1]。所以需要一个合适的映射：
  $$pixel=\frac{normal+1}{2}$$
  同样地，当我们从法线纹理采样时，我们需要进行如下逆映射：
  $$normal=pixel\times 2-1$$
  那么，我们为什么要把***切线空间***的法向量存入法线纹理中呢？模型空间不行吗？世界空间不行吗？
  
  对于着色计算而言，一般都是在世界空间进行的。考虑到直观性，模型空间却更好。但是对于凹凸映射而言，选择切线空间有如下好处：
  • 自由度高。对于模型空间或其他空间而言，法线信息是绝对的，而切线空间是相对的，取决于该顶点的法线和切线方向。这就意味着，绝对法线仅仅适用于创建它的初始模型，对于其他模型网格，就会有失真的情况。但是对于切线空间的法线纹理信息而言，其值其实是一个“扰动值”，也就是说并不是该点真实的法向量，而是用于着色计算时使用的法线值，是对该顶点法线的计算层面的扰动。这就意味着，当我们将这张贴图用于其他模型上时，也可以保证一定的效果。
  • 保证UV动画正常进行。当我们移动UV坐标实现UV动画时，相当于给新模型贴图，如上所述，绝对的法线信息就无法达到正确效果。
  • 可以复用法线纹理，通过扰动达到不通效果。
  • 可以压缩，由于切线空间法线永远是外法线，z分量永远为正，可由xy推导出来。所以我们可以将法线贴图中某个通道空出，达到压缩的目的，当然，也可以存储其他模型信息。
    对于法线纹理而言，由于大部分位置的法线与模型原法线一致，为(0,0,1)，经过映射之后，变为了(0.5,0.5,1)是浅蓝色，所以法线纹理的视觉特征就是大片大片的蓝色。
    

高度图转化为法线贴图的数学方法

基本方法：利用高度图每个相邻像素平直表面的高度差，计算$s$和$t$方向上的切向量，用$H(i,j)$表示尺寸为$w\times h$像素的高度图在$<i,j>$处的高度值，则：
$$S(i,j)=<1,0,aH(i+1,j)-aH(i-1,j)>$$
$$T(i,j)=<0,1,aH(i,j+1)-aH(i,j-1)>$$
$a$为比例系数，可修改高度值范围，控制扰动程度。
$$N(i,j)=\frac{S(i,j)\times T(i,j)}{||S(i,j)\times T(i,j)||}=\frac{<-S_z,-T_z,1>}{\sqrt{S_z^2+T_z^2+1}}$$

实战代码(这里不列出世界空间算法)

Shader "Unity Shaders Book/Chapter 7/Normal Map In Tangent Space"{
    Properties{
        _Color ("Color Tint",Color)=(1,1,1,1)
        _MainTex ("MainTex",2D)="white" {}
        _BumpMap ("NormalMap",2D)="bump" {} //法线纹理贴图
        _BumpScale ("BumpScale",Float)=1.0  //控制凹凸程度
        _Specular ("Specular",Color)=(1,1,1,1)
        _Gloss ("Gloss",Range(8.0,256))=20
    }

    SubShader{
        pass{
            Tags{"LightMode"="ForwardBase"}
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "Lighting.cginc"

            fixed4 _Color;
            sampler2D _MainTex;
            float4 _MainTex_ST;
            sampler2D _BumpMap;
            float4 _BumpMap_ST;
            float _BumpScale;
            fixed4 _Specular;
            float _Gloss;

            struct a2v{
                float4 vertex:POSITION;
                float3 normal:NORMAL;
                float4 tangent:TANGENT;//切线的w分量代表切线方向，后续乘积代表选择切线坐标系方向
                float4 texcoord:TEXCOORD0;
            };

            struct v2f{
                float4 pos:SV_POSITION;
                float4 uv:TEXCOORD0;
                float3 lightDir:TEXCOORD1;
                float3 viewDir:TEXCOORD2;
            };

            v2f vert(a2v v){
                v2f o;
                o.pos=UnityObjectToClipPos(v.vertex);

                o.uv.xy=v.texcoord.xy*_MainTex_ST.xy+_MainTex_ST.zw;//纹理坐标变换
                o.uv.zw=v.texcoord.xy*_BumpMap_ST.xy+_BumpMap_ST.zw;//法线贴图坐标变换

                float3 binormal=cross(normalize(v.normal),normalize(v.tangent.xyz))*v.tangent.w;//两个单位向量在相互垂直的时候，叉乘也是单位向量
                float3x3 rotation=float3x3(v.tangent.xyz,binormal,v.normal);//求出变换矩阵，三个分量是按行排列的，符合float3x3的传统，要保证三个分量是单位向量，这样构成的转置矩阵才是逆矩阵

                o.lightDir=mul(rotation,ObjSpaceLightDir(v.vertex)).xyz;
                o.viewDir=mul(rotation,ObjSpaceViewDir(v.vertex)).xyz;

                return o;
            }

            fixed4 frag(v2f i):SV_TARGET{
                fixed3 tangentLightDir=normalize(i.lightDir);
                fixed3 tangentViewDir=normalize(i.viewDir);

                fixed4 packedNormal=tex2D(_BumpMap,i.uv.zw);
                fixed3 tangentNormal;

                //if the texture is not marked as "Normal Map"
                //tangentNormal.xy=(packedNormal.xy*2-1)*_BumpScale;
                //tangentNormal.z=sqrt(1.0-saturate(dot(tangentNormal.xy,tangentNormal.xy)));

                //or
                tangentNormal=UnpackNormal(packedNormal);//UnpackNormal实现逆映射，这里的法线自然是单位向量
                tangentNormal.xy*=_BumpScale;//控制扰动程度
                tangentNormal.z=sqrt(1.0-saturate(dot(tangentNormal.xy,tangentNormal.xy)));

                fixed3 albedo=tex2D(_MainTex,i.uv).rgb*_Color.rgb;
                fixed3 ambient=UNITY_LIGHTMODEL_AMBIENT.xyz*albedo;
                fixed3 diffuse=_LightColor0.rgb*albedo*max(0,dot(tangentNormal,tangentLightDir));
                fixed3 halfDir=normalize(tangentLightDir+tangentViewDir);
                fixed3 specular=_LightColor0.rgb*_Specular.rgb*pow(max(0,dot(tangentNormal,halfDir)),_Gloss);

                return fixed4(ambient+diffuse+specular,1.0);
            }
            ENDCG
        }
    }
    Fallback "Specular"
}

效果图：