浅谈后缀数组 + 模板

 

 

 

 

 

 

--------- 以上来自 https://blog.csdn.net/YxuanwKeith/article/details/50636898

 

 

 

---------以上来自 https://www.cnblogs.com/victorique/p/8480093.html

---

一些我的理解

刚刚学了后缀数组 , 认为造成我理解的最大的困难点就是对rank , sa 数组 以及其余辅助数组的概念不清, 这里来区分一下

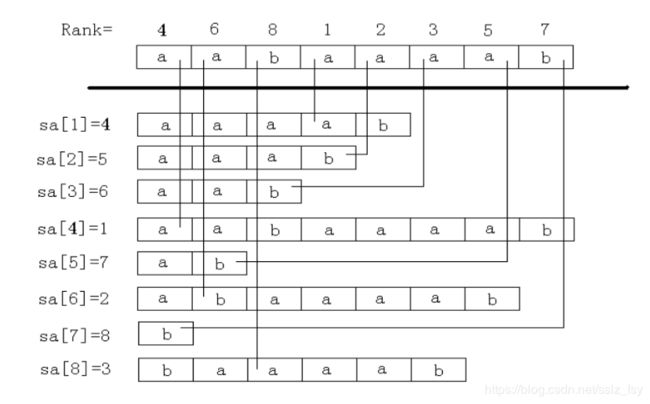
SA[i] : 表示排名为i的后缀的开始位置 

rank[i] : 表示后缀开始位置为i 的排名

也就是说 SA[rank[i]] = rank[SA[i]] = i , 这两个配合有很多用途

例如: SA[rank[i]-1] 就是i 前面一名的后缀的起始位置 , 在图中来看 , 要找aaab 的前一名 , 就是SA[rank[5]-1] = 4

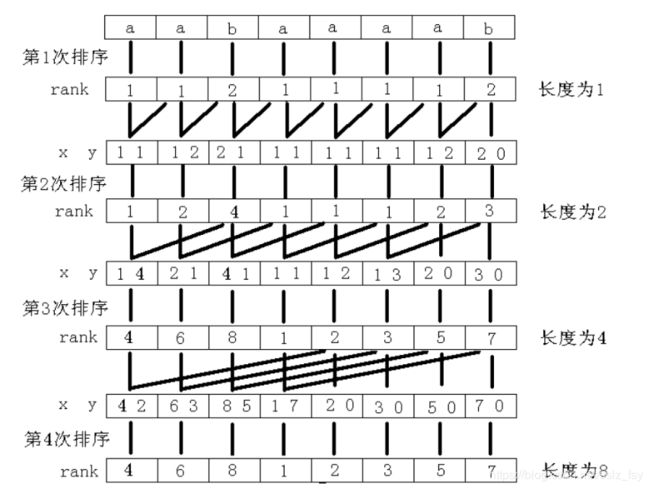
y[i] ( 排序第二关键字) : 表示的是第二关键字为i 的位置 , 例如第3次排序时

y数组可能是: 7,8,2,3,4,5,6,1 (按这个顺序输出第二关键字就是 0 0 1 1 1 2 3 4)

c[i] (桶) : 表示现有元素出现次数 , 如第一次排序 , c[a] = 5 , c[b] = 3

我们将c 求一个前缀和 , c[a] = 5 , c[b] = 8 . 这样一来 以b开头的第二关键字最大的的排名就是8

以a开头的第二关键字最大的就是5

tmp[i] : 辅助数组 , 将x copy 一遍 , 理解为离散化时的另一个数组

---

模板

#include
#define N 1000050
using namespace std;
char s[N]; int rank[N],y[N],tmp[N]; 
int c[N],SA[N],n,m,Height[N];
void Sort(){
	for(int i=1;i<=m;i++) c[i] = 0;
	for(int i=1;i<=n;i++) c[rank[i]]++;
	for(int i=2;i<=m;i++) c[i] += c[i-1];
	for(int i=n;i>=1;i--) SA[c[rank[y[i]]]--] = y[i];
}
void get_SA(){
	for(int i=1;i<=n;i++) rank[i] = s[i] , y[i] = i;
	Sort();
	for(int k=1;k<=n;k<<=1){
		int cnt = 0;
		for(int i=n-k+1;i<=n;i++) y[++cnt] = i;
		for(int i=1;i<=n;i++) if(SA[i]>k) y[++cnt] = SA[i] - k;
		Sort(); swap(rank,tmp); int num = 1; rank[SA[1]] = 1;
		for(int i=2;i<=n;i++){
			if(tmp[SA[i]] == tmp[SA[i-1]] && tmp[SA[i]+k] == tmp[SA[i-1]+k])
				rank[SA[i]] = num;
			else rank[SA[i]] = ++num;
		} m = num;
	}
}
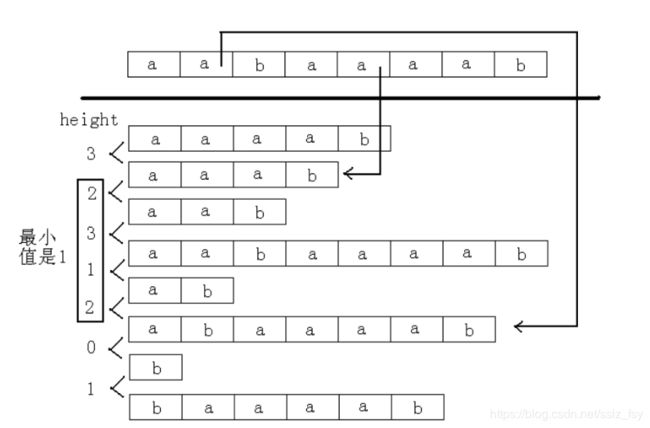
void get_Hi(){
	int k = 0;
	for(int i=1;i<=n;i++){
		if(rank[i]==1) continue;
		int j = SA[rank[i]-1]; if(k) k--;
		while(i+k<=n && j+k<=n && s[i+k]==s[j+k]) k++; 
		Height[rank[i]] = k;
	}
} 
int main(){
	scanf("%s",s+1); n = strlen(s+1);
	m = 127; get_SA();  get_Hi();
	for(int i=1;i<=n;i++) printf("%d ",SA[i]);
	return 0;
}