普里姆算法-prim

算法代码：

 C++ Code 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49

/* Prim算法生成最小生成树  */ void MiniSpanTree_Prim(MGraph MG) {      int min, i, j, k;      int adjvex[MAXVEX]; /* 保存相关顶点下标 */      int lowcost[MAXVEX]; /* 保存相关顶点间边的权值 */     lowcost[ 0] =  0; /* 初始化第一个权值为0，即v0加入生成树 */      /* lowcost的值为0，在这里就是此下标的顶点已经加入生成树 */     adjvex[ 0] =  0; /* 初始化第一个顶点下标为0 */     cout <<  "最小生成树的边为：" << endl;      for (i =  1; i < MG.numVertexes; i++)     {         lowcost[i] = MG.arc[ 0][i]; /* 将v0顶点与之有边的权值存入数组 */         adjvex[i] =  0; /* 初始化都为v0的下标 */     }      for (i =  1; i < MG.numVertexes; i++)     {         min = INFINITY;  /* 初始化最小权值为∞， */         j =  1;         k =  0;          while (j < MG.numVertexes) /* 循环全部顶点 */         {              if (lowcost[j] !=  0 && lowcost[j] < min) /* 如果权值不为0且权值小于min */             {                 min = lowcost[j]; /* 则让当前权值成为最小值 */                 k = j; /* 将当前最小值的下标存入k */             }             j++;         }         cout <<  "(" << adjvex[k] <<  ", " << k <<  ")" <<  "  ";  /* 打印当前顶点边中权值最小的边 */         lowcost[k] =  0; /* 将当前顶点的权值设置为0,表示此顶点已经完成任务 */          for (j =  1; j < MG.numVertexes; j++) /* 循环所有顶点 */         {              /* 如果下标为k顶点各边权值小于此前这些顶点未被加入生成树权值 */              if (lowcost[j] !=  0 && MG.arc[k][j] < lowcost[j])             {                 lowcost[j] = MG.arc[k][j]; /* 将较小的权值存入lowcost相应位置 */                 adjvex[j] = k; /* 将下标为k的顶点存入adjvex */             }         }     }     cout << endl; }

1、程序中1~16行是初始化操作，其中第7～8行 adjvex[0] = 0 意思是现在从顶点v0开始（事实上从那一点开始都无所谓，假定从v0开始），lowcost[0]= 0 表示v0已经被纳入到最小生成树中，之后凡是lowcost数组中的值被设为0就表示此下标的顶点被纳入最小生成树。

2、第11～15行表示读取邻接矩阵的第一行数据，所以 lowcost数组为{ 0 ,10, 65535, 65535, 65535, 11, 65535, 65535, 65535 }，而adjvex数组为全0。至此初始化完毕。

3、第17~49行共循环了8次，i从1一直累加到8，整个循环过程就是构造最小生成树的过程。

4、第24～33行，经过循环后min = 10, k = 1。注意26行的if 判断lowcost[j] != 0 表示已经是生成树的顶点则不参加最小权值的查找。

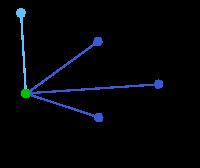
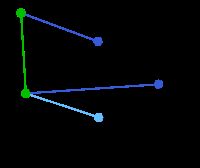
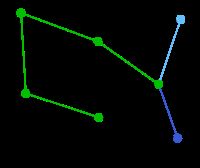
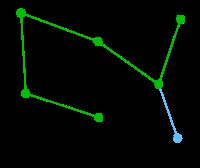
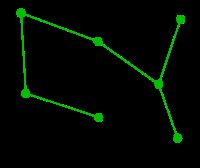
5、第35行，因k = 1, adjvex[1] = 0, 所以打印结果为(0, 1)，表示v0 至 v1边为最小生成树的第一条边，如下图的第一个小图。

6、第36行，因k = 1 将lowcost[k] = 0 就是说顶点v1纳入到最小生成树中，此时lowcost数组为{ 0,0, 65535, 65535, 65535, 11, 65535, 65535, 65535 }

7、第38～47行，j 循环从1 到8， 因k = 1，查找邻接矩阵的第v1行的各个权值，与lowcost数组对应值比较，若更小则修改lowcost值，并将k值存入adjvex数组中。所以最终lowcost = { 0,0, 18, 65535, 65535, 11, 16, 65535, 12 }。 adjvex数组的值为 {0, 0, 1, 0, 0, 0, 1, 0, 1 }。这里的if判断也表示v0和v1已经是生成树的顶点不参与最小权值的比对了。

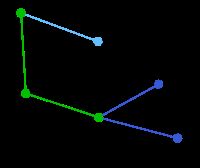
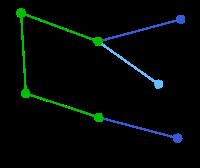
上面所述为第一次循环，对应下图i = 1的第一个小图，由于要用文字描述清楚整个流程比较繁琐，下面给出i为不同值一次循环下来后的生成树图示，所谓一图值千言，大家对着图示自己模拟地循环8次就能理解普里姆算法的思想了。

即最小生成树的边为：(0, 1), (0, 5), (1, 8), (8, 2), (1, 6), (6, 7), (7, 4), (7, 3)

最后再来总结一下普里姆算法的定义：

假设N = （V{E} ）是连通网，TE是N上最小生成树的集合。算法从U = { u0} ( uo V)，TE = { } 开始。重复执行下述操作：在所有

uU，v V - U 的边（u, v) E 中找一条代价最小的边(u0 , v0) 并入集合TE, 同时v0 并入U, 直至 U = V 为止。此时TE 中必有n-1 条边， 则 T = （V，{TE} ) 为N的最小生成树。

下面附一个图例，模拟图的最小生成树的产生过程：

图例	说明	不可选	可选	已选
	此为原始的加权连通图。每条边一侧的数字代表其权值。	-	-	-
	顶点D被任意选为起始点。顶点A、B、E和F通过单条边与D相连。A是距离D最近的顶点，因此将A及对应边AD以高亮表示。	C, G	A, B, E, F	D
	下一个顶点为距离D或A最近的顶点。B距D为9，距A为7，E为15，F为6。因此，F距D或A最近，因此将顶点F与相应边DF以高亮表示。	C, G	B, E, F	A, D
	算法继续重复上面的步骤。距离A为7的顶点B被高亮表示。	C	B, E, G	A, D, F
	在当前情况下，可以在C、E与G间进行选择。C距B为8，E距B为7，G距F为11。E最近，因此将顶点E与相应边BE高亮表示。	无	C, E, G	A, D, F, B
	这里，可供选择的顶点只有C和G。C距E为5，G距E为9，故选取C，并与边EC一同高亮表示。	无	C, G	A, D, F, B, E
	顶点G是唯一剩下的顶点，它距F为11，距E为9，E最近，故高亮表示G及相应边EG。	无	G	A, D, F, B, E, C
	现在，所有顶点均已被选取，图中绿色部分即为连通图的最小生成树。在此例中，最小生成树的权值之和为39。	无	无	A, D, F, B, E, C, G

由算法代码中的循环嵌套可得知此算法的时间复杂度为O(n^2)。

对比普里姆和克鲁斯卡尔算法，克鲁斯卡尔算法主要针对边来展开，边数少时效率比较高，所以对于稀疏图有较大的优势；而普里姆算法对于稠密图，即边数非常多的情况下更好一些。