1.数组

数组的索引按照32位且无符号定点整数存储，也就是说数组索引最大值为 2³²，而数组以0开始，所以实际最大值为2³² - 1

数组

2.位运算符

位运算符

位运算只对整数起作用，如果一个运算子不是整数，会自动转为整数后再运行。虽然在 JavaScript 内部，数值都是以64位浮点数的形式储存，但是做位运算的时候，是以32位带符号的整数进行运算的，并且返回值也是一个32位带符号的整数。

对于 & | ^ ~ 以后单独再说,主要说明 <<, >>, >>>

上表定义的补充说明：
算数运算
<< 表示有符号位左移，忽略正负数，右边都用0填充；
>> 表示有符号位右移，如果该数为正，则高位补0，若为负数，则高位补1，丢弃被移出的位；
逻辑运算
>>> 表示无符号右移，也叫逻辑右移，即若该数为正，则高位补0,
而若该数为负数，则右移后高位同样补0。
(注：
有符号位位移代表，符号位不变，数值位移动；
无符号位位移代表，符号位与数值位一起移动；
负数在位运算时转换成的32位2进制数使用补码表示法
)

[<<, >>] ：以实际的32位的数值 3 和 -3 为例：
0000 0000 0000 0000 0000 0000 0000 0011
1111 1111 1111 1111 1111 1111 1111 1101   

若，进行 3 << 2 ，-3 << 2 的运算，即得
0000 0000 0000 0000 0000 0000 0000 1100 == 12（右边用0填充）
1111 1111 1111 1111 1111 1111 1111 0100 == -12（右边用0填充）

若，进行 12 >> 3，-12 >> 3 的运算，即得
0000 0000 0000 0000 0000 0000 0000 0001 == 1（丢弃被移出的位）
1111 1111 1111 1111 1111 1111 1111 1110 == -2 （丢弃被移出的位，高位补1）

若，进行 3 >> 1，-3 >> 1的运算，即得
0000 0000 0000 0000 0000 0000 0000 0001 == 1（丢弃被移出的位）
1111 1111 1111 1111 1111 1111 1111 1110 == -2 （丢弃被移出的位，高位补1）
(这里应该会有人疑惑了，思维惯性会让人误以为 -12 >> 3 应该是 -1，但是结果却是-2，
这是由于补码的性质所致，所以在不清楚补码的前提下不建议使用位运算，
因为很多人喜欢用 << >> 去代替Math.pow(2, x) ，看似大部分运算都能得到想要的值，
这是在挖坑。但不得不说位运算是原始运算，所以运算速度更快。

[维基百科：位操作是程序设计中对位模式或二进制数的一元和二元操作。在许多古老
的微处理器上，位运算比加减运算略快，通常位运算比乘除法运算要快很多。在现代架
构中，情况并非如此：位运算的运算速度通常与加法运算相同（仍然快于乘法运算）。]

如果你一定要使用，请注意
1、正数奇数、负数 的 >> 运算的结果可能与预期不符（Math.pow(2, x) ）；
2、位运算得出的一定是整数，不会有小数，因为小数会被忽略；
3、正负纯小数的位运算都为 0，因为小数会被忽略；
4、如果值 >= 32，如：1 << 32 , 会隐式转换成 1 << 32 % 32 ；
5、右移按照规则进行，左移符号位会被替换掉；
6、位移值为31会怪异，如：1 << 31；
0000 0000 0000 0000 0000 0000 0000 0001
按照定义，有符号位位移，符号位不变，数值位移动，应得
0000 0000 0000 0000 0000 0000 0000 0000  == 0
但是，实际输出的值为 -2147483648, 他的32位有符号二进制补码表示为
1000 0000 0000 0000 0000 0000 0000 0000
在看，2147483647 << 1 （2147483647 = 2^31-1）
0111 1111 1111 1111 1111 1111 1111 1111 (2147483647的二进制)
1111 1111 1111 1111 1111 1111 1111 1110 == -2 （移位后的二进制和十进制）
可见，符号位还是被进位了，这对于高程中的说明有出入。这点需要注意。
)

总之，不清楚二进制不建议使用

[>>>] ：以32位的数值 1 和 -1 为例：
0000 0000 0000 0000 0000 0000 0000 0001
1111 1111 1111 1111 1111 1111 1111 1111
若，进行 1 >>> 1，-1 >>> 1 的运算，即得
0000 0000 0000 0000 0000 0000 0000 0000 == 0
0111 1111 1111 1111 1111 1111 1111 1111 == 2147483647

ECMA相关位运算说明

带号右移位运算符（>>）

产生式 ShiftExpression : ShiftExpression >> AdditiveExpression 按照下面的过程执行 :
1.令 lref 为解释执行 ShiftExpression 的结果 .
2.令 lval 为 GetValue(lref).
3.令 rref 为解释执行 AdditiveExpression 的结果 .
4.令 rval 为 GetValue(rref).
5.令 lnum 为 ToInt32(lval).
6.令 rnum 为 ToUint32(rval).
7.令 shiftCount 为用掩码算出 rnum 的最后五个比特位 , 即计算 rnum & 0x1F 的结果。
8.返回 lnum 带符号扩展的右移 shiftCount 比特位的结果 . 缺少的比特位填零. 结果是一个有符号 32 位整数。

ToInt32()：转化为有符号 32 位整数
ToUint32()：转化为无符号 32 位整数
GetValue()： ECMAscript 8.7.1 (个人理解在这里，只要不能转化成数字的，都以0处理)
掩码： （英语：Mask）在计算机学科及数字逻辑中指的是一串二进制数字，通过与目标数字的按位操作达到屏蔽指定位而实现需求。
rnum & 0x1F == 右操作数 & 11111(二进制) == 右操作数 % 32

完整的位运算步骤


"4294967299.8" >> 1 （4294967299.8 = 2^32 + 3 + 0.8）
① 把操作数 "4294967299.8" 强制转化成Number类型，这就可能得到NaN，
（位运算会将NaN、Infinity、-Infinity都转换成0）并且会忽略小数部分，
相当于进行了 parseInt( Number( "4294967299.8" ) ) 操作，得到 4294967299。
又因为要转换成有符号32位整型（原码形式），相当于Math.abs(4294967299)，
得到 4294967299
② 把 4294967299 转化成 2进制
1 0000 0000 0000 0000 0000 0000 0000 0011
③ 超过 32 位的 2进制数要舍弃。（特别注意，这里的舍弃是从左边开始）
0000 0000 0000 0000 0000 0000 0000 0011
④ 根据 第一个操作数 的正负来决定此 2进制 是否各位取反，然后 + 1。
因为 4294967299 为正数 ，所以不做转化 （对于绝对值>= 2^31 的数，这里是天坑）
0000 0000 0000 0000 0000 0000 0000 0011 （此时的2进制已经为补码表示法，很重要）
⑤ 根据数 1 进行移位操作。如果该数为正，则高位补0，若为负数，则高位补1，丢弃被移出的位
0000 0000 0000 0000 0000 0000 0000 0001
⑥ 将此 2 进制数的补码形式转换成原码形式，在转换成 10 进制
0000 0000 0000 0000 0000 0000 0000 0001 = 1

根据此步骤带入一些特殊值
6442450947 >> 0  （6442450947= 2^32 + 2^31 + 3）
① 6442450947
② 1 1000 0000 0000 0000 0000 0000 0000 0011
③ 1000 0000 0000 0000 0000 0000 0000 0011 
④ 根据 第一个操作数 的正负来决定此 2进制 是否各位取反，然后 + 1
因为 6442450947 为正数 ，所以不做转化 （对于绝对值>= 2^31 的数，这里是天坑）
1000 0000 0000 0000 0000 0000 0000 0011（此时的2进制已经为补码表示法，很重要）
⑤ 根据 第二个操作数 0 进行移位操作。
1000 0000 0000 0000 0000 0000 0000 0011（补码）
⑥ 那么对应的原码就是
1111 1111 1111 1111 1111 1111 1111 1101（原码）= -2147483645

-6442450947 >> 0  
① 6442450947
② 1 1000 0000 0000 0000 0000 0000 0000 0011
③ 1000 0000 0000 0000 0000 0000 0000 0011 
④ 根据 第一个操作数 的正负来决定此 2进制 是否各位取反，然后 + 1。
因为 -6442450947 为负数 ，所以转化 （对于绝对值>= 2^31 的数，这里是天坑）
0111 1111 1111 1111 1111 1111 1111 1101（此时的2进制已经为补码表示法，很重要）
⑤ 根据 第二个操作数 0 进行移位操作。
0111 1111 1111 1111 1111 1111 1111 1101（补码）
⑥ 那么对应的原码就是
0111 1111 1111 1111 1111 1111 1111 1101（原码）= 2147483645

-1024 >> 2  （1024 = 2^10 ）
① 1024
② 0000 0000 0000 0000 0000 0100 0000 0000
③ 0000 0000 0000 0000 0000 0100 0000 0000
④ 根据 第一个操作数 的正负来决定此 2进制 是否各位取反，然后 + 1。
因为 -1024 为负数 ，所以得出
1111 1111 1111 1111 1111 1100 0000 0000 （此时的2进制已经为补码表示法，很重要）
⑤ 根据 第二个操作数 2 进行移位操作。
1111 1111 1111 1111 1111 1111 0000 0000（补码）
⑥ 对应的原码就是
1000 0000 0000 0000 0000 0001 0000 0000（原码）= -256

（以上为个人分析求证后结果，完全没有权威性。。）

3.数字计算

js能精确计算（运算结果）的数值范围是 [-2⁵³, +2⁵³ ]
js能表示的纯整数数值范围是 [-1.8x10³⁰⁸ , +1.8x10³⁰⁸]
js能表示的纯小数数值范围是 [ -5x10^-324, -1) ∪ (+1, 5x10^-324 ]

数值轴

IEEE754

IEE754标准就和js中的正则表达式，unicode编码一样，他不是js特有的东西的，而是一种国际上通用规范，
目的其一，方便；
目的二，使程序可移植性强。
（在js中定义的数值，解释器会帮我们把值转化为IEEE754标准的64位浮点型，如果是位运算，解释器会把值定义为32位整型）

了解他之前，先看一个示例

我们以8位定点数原码表示
>>>>整数为例：
0111 1111 == 127  (最大正值)
0000 0001 == 1  (最小正值)

0000 0000 == 0  
1000 0000 == -0 

1111 1111 == -127（绝对值最大负值）
1000 0001 == -1 （绝对值最小负值）

>>>>小数为例：
0111 1111 == 0.9921875  (最大正值小数)
0000 0001 == 0.0078125  (最小正值小数)

0000 0000 == 0 
1000 0000 == -0

1111 1111 == -0.9921875  (绝对值最大负值小数)
1000 0001 == -0.0078125  (绝对值最小负值小数)
(说明：这里表示的小数最大最小范围并不准确，只是为了直观。比如：
0111 1111 == 0.9921875
0111 1110 == 0.984375   
那么 0.984375 < x < 0.9921875  中的间隙值 x 是无法表示的。
下示补码同理
)

我们以8位定点数补码表示
>>>>整数为例：
0111 1111 == 127  (最大正值)
0000 0001 == 1  (最小正值)

0000 0000 == 0  
1000 0000 == -128 

1000 0001 == -127（绝对值最大负值）
1111 1111 == -1 （绝对值最小负值）

>>>>小数为例：
0111 1111 == 0.9921875  (最大正值小数)
0000 0001 == 0.0078125  (最小正值小数)

0000 0000 == 0 
1000 0000 == -1

1000 0001 == -0.9921875  (绝对值最大负值小数)
1111 1111 == -0.0078125  (绝对值最小负值小数)

*补码即使比源码多表示一个值，也就仅仅表示2的8次方个数*
由此可见，使用定点数表示问题如下：
1.一条数据，要么表示整数，要么就表示小数，表示类似 25.375 的值需要特殊处理。
2.无法使用现有位数满足更大的值的需求。
3.间隙值需要补充机器位数进行填充。
4.对于类似+(-)0.000001的真值要保存过多的0，浪费存储空间，
且降低精度。

那么，我们能不能创造出一种，利用有限的8位机器数，尽可能多的解决上述问题的方法呢？

在数学里，对于较大的值我们可以使用科学计数法的方式进行表示，如：
14500000000 == 1.45 x 10¹⁰
显然科学记数法更简单直观，我们可以利用这一特性对2进制编码进行自定义

假设，机器位为8，有如下的一段2进制编码：

胡编乱造的8位浮点数表示法 1-1

我们自己把2进制编码定义成了3部分（定点数只把2进制编码分成2部分， 符号位 和 数值位），作如下约定：

符号位：0表示正值， 1表示负值；
指数位：就是我们理解的平方数，在这里由于是2进制，所以，指数位的010暂且表示为 2⁰¹⁰ = 2² ，且指数的表示范围为0 ~ 7之间。（一会说这样做的问题）
数值位：就是我们要表示的真实的值的部分，但是，这里的1010并不是我们通常理解的10进制的10，因为我们要在这解决上述定点数的问题,

问题1：定点表示中，只有两个相关硬件，整数定点机，和小数定点机。一条数据，要么表示整数，要么就表示小数。

那么，我们怎么设计才能让一条整数，小数共存的数据表示在一个硬件中呢？且简单易懂？

我们把1010想象成一个定点小数，且我们约定，数值位前默认有（0.），那么他的数值位实际值为
0.1010
然后再乘以指数部分的 010 ，得
0.1010 x 2⁰¹⁰ == 0.1010 x 2² == 10.10(二进制) == 2.5(十进制) =>符号位为0，所以最后，
根据我们的自定义规则解码后的 0010 1010 二进制编码的值为 + 2.5

根据上述操作，我们解决了整数，小数共存的二进制编码的问题。

但是，以（0.）作为约定的数值位默认头是有问题的，比如：
真值 +0.001010 以我们自定义规则转换成的二进制为,
0000 0010 ，因为机器位数为8，超过的8位要舍去，10就被丢掉了，损失了精度且保留了多余的，没有意义的0 。
这就引出了我们要解决的问题4

问题4：对于类似+(-)0.000001的真值要保存过多的0，浪费存储空间，且降低精度。

看来，我们现在需要对规则进行一些修改，我们尝试以（1.）作为约定的数值位默认头，还是以真值 +0.001010为例，那么这个真值可以改写为
1.010 x 2^-3 == 1.010 x 2^-011

这回可操蛋了，因为之前我们约定的指数部分的表示范围是0 ~ 7，这个-3可怎么办呢，聪明的你肯定想到了，何不把指数位置的第一位也规定为符号位呢？这不就可以表示正负数了吗，没错，是可以满足需求，但是，多一个符号位的判断会增加机器的运算复杂度负担，那么可以用补码啊？没错，但是，如果通过指数进行数值比较的时候（注意：在对两个值进行判断的时候，例如 3 > 4，计算机浮点运算器会对 3 和 4 对应的64位浮点数指数位数值进行比较，如果不相等，直接返回true或false，如果想等，再进行数值位的比较），又要增加负担，有没有更好的办法呢？

指数数轴

如图所示，我们可以把负数也当做正数表示，然后用表示的值 + 偏移值就是实际的指数值
偏移值: 2 ^k / 2 - 1 == 2 ^k-1 - 1 (k为指数的位数)
所以，对于我们的规则中，指数偏移值 == 2 ^3-1 - 1 == 3 == 011
(在计算机机器数表示法中,有一种移码表示法,和它非常类似)

>>>移码表示法非常的简单
x(移) = 2^n + x(真)  [注:n为数值位的个数,不包括符号位]
例: 字长6位机器中,符号1位,数值5位
真值a = +10101(十进制 +21) , 
真值b = -10101(十进制 -21)
那么
真值a对应的移码为: a(移) = +10101 + 2^5(100000) = 110101
真值b对应的移码为: b(移) = -10101 + 2^5(100000) = 001011
可以直接根据编码判断出 a > b

如果是补码
真值a对应的补码为: a(补) = +10101 = 010101
真值b对应的补码为: b(补) = -10101 = 101011
可以直接根据编码判断出 b > a (错的)

百度百科解释:移码（又叫增码）是符号位取反的[补码]，一般用做浮点数的阶码，
引入的(主要)目的是为了保证浮点数的机器零为全0。
次要目的:在计算机中,大部分运算都采用补码,但是补码表示法很难直接判断对应的真值的大小,
上面我们已经证实过.

偏移值: 2^k-1 - 1 (k为指数的位数)  == 移码 - 1
移码表示法和移位运算不是一个东西,注意区分

可推理出
真值 +0.001010 == 1.010 x 2^-3 == 1.010 x 2^-011
得指数真实表示的值为 -011 + 偏移值 011 == 000
真值 +0.001010 的自定义2进制编码值为
0000 0100

经过以上的求证，得到新的8位机器数浮点数约定如下：

符号位：0表示正值， 1表示负值；
指数位：表示-3(000) ~ 4(111) 的指数，偏移值为 3；
数值位：通过进位/退位得到的 1.（..........）的括号内的值

所以，图1-1使用我们新约定的浮点数规则解码，得到：
1.1010 x 2^010-011=-1 == 0.11010
+0.11010 == 0.9140625

那么其实，问题2，3也解决了

先说间隙值

所有的小数我们都能用浮点数表示，只不过由于数值位的限制，精度会有损耗，所以，数值位越多，精度就越高，但是数值位与指数位是互补的，数值位多，指数位就会少，指数位少了，能够表示的数值范围就会小，反之亦然。

再说数值范围

8位定点数
0111 1111 == 127 (最大正值)
8位自定义浮点数
0111 1111 == 1.1111 x 2^111-011=4 == 11111 == 31 （最大正值）
怎么还小了呢？这是因为 8位机器数本身的限制，这里只能使用更高的16位机器数来说明
16位整数定点数
0111 1111 1111 1111 == 32767 (最大正值)
16位自定义浮点数
设，符号位1，指数位6，数值位 9 ，偏移值 2⁵ - 1 == 31
0111 1111 1111 1111 == 1.1111 1111 1 x 2³² (最大正值)
== 1111 1111 1100 0000 0000 0000 0000 0000 0 == 8581545984

32767 和 8581545984 比较，很直观的体现了数值范围，而且，我们得知
机器位数越小，越不适用浮点数表示法；
机器位数越大，越适用浮点数表示法；

我们再回过头来看看IEEE754,由于js使用的是IEEE754双精度浮点格式（64 位），所以我们就针对64位说明。其实，和我们上面自己胡编乱造的规则基本一样，

IEEE754双精度浮点格式
符号位1，指数位11，数值位52，偏移值 2^11-1 - 1 == 1023

但是！

指数位和我们自定义规则有些不同，他把全0和全1的情况，单独拿出来干别的了。也就是说本来我们有2048 个可用数
0000 0000 000 ~ 1111 1111 111 (指数可表示值范围-1023 ~ 1024)
现在只有2046个可以用了
0000 0000 001 ~ 1111 1111 110 (指数可表示值范围-1022 ~ 1023)

说明:以下使用的图片用单精度32位来表示，因为64位实在是太长了。。
单精度32位：符号位 1，指数位 8，数值位 23，指数范围 -126 ~ 127

那他到底拿这两个特殊指数干啥了呢？

先说全指数位全1（称为：特殊数值）

Ⅰ.不管符号位，当指数位全位1，数值位不为0时，表示我们最怕见到的 NaN

产生NaN情况为：

注意这是标准自身定义的场景，不要与parseInt等js方法产生的NaN混淆。（REM为模运算）

Ⅱ.当指数位全位1，数值位为0时，表示无穷 ;
符号位为0，代表 + Infinity
符号位为1，代表 - Infinity

再说指数位全0（称为：非格式化数值）

Ⅰ.前面提到，在数值位前面有一个隐藏头（1.），这使得我们没有办法表示 0 这个真值，所以IEEE754遵循了传统的二进制编码全0方式来代表0
（但是，由于符号位保留，所以就有了 +0 和 -0之分，查阅资料说+0 和 -0还是有些区别的，到底有什么区别日后在研究，但是在javascript中，+0 和 -0 是全相等的，所以不用担心0的运算）
所以，当指数位，数值位都为0时，代表真值0

个人认为，为了表示真值0，是IEEE754出现非格式化数值的主要原因。非格式化就是把隐藏头（1.）改成（0.）

Ⅱ.那么，当指数位为0，数值位不为0呢？这块闲置的区域你总得干点什么吧，不然就浪费了啊，就比如下图

注意，非格式化把隐藏头（1.）改成（0.）

这块区域的值用来表示比 1.0 x 2 ^-126 （64位就是1.0 x 2 ^-1022）更小的值。
表示方法为 1.0 x 2^-126 x 数值部分
那么其实上图表示的的实际值为：
1.0 x 2 ^-126 x 0.00000000000000000000001
== 1.0 x 2 ^-126 x 1.0 x 2 ^-23 == 1.0 x 2 ^-149 (2进制)
== 1.4 x 10 ^-45(10进制)

这也是IEEE754单精度（32位）能表示的绝对值最小的数。
那么IEEE754双精度（64位）能表示的绝对值最小的数为：
1.0 x 2 ^-1022 x 0.0000000000000000000000000000000000000000000000000001
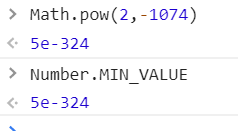
== 1.0 x 2 ^-1022 x 1.0 x 2 ^-52 == 1.0 x 2 ^-1074 (2进制)
== 5 x 10 ^-324(10进制)

我们和js中的实际最小值进行对比

现在，我们可以自己证明

js能精确计算的数值范围是 -2⁵³ ~ 2⁵³

因为数值位是52位，加上约定的隐藏头1. 那么就是 53位，超出的部分舍弃，所以就是精度损失
但严谨来说，应该是不包含小数

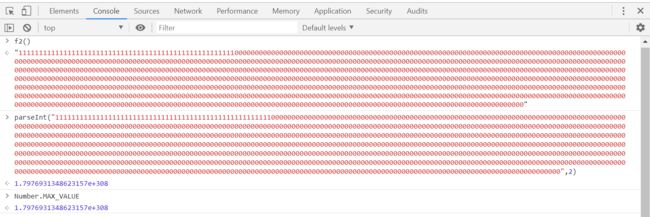
js能表示的纯整数数值范围是 -1.8x10³⁰⁸ ~ 1.8x10³⁰⁸

>>>>
0111 1111 1110 1111 1111 1111 1111 1111
1111 1111 1111 1111 1111 1111 1111 1111 
~
1111 1111 1110 1111 1111 1111 1111 1111 
1111 1111 1111 1111 1111 1111 1111 1111

function f2(){
    let str = '1'
    for(let i = 0;i<1023;i++){
        if(i < 52) str += '1';
        else str += '0';
    }
    return str
 }

js能表示的纯小数数值范围是（-1< ~ -5x10^-324）和（5x10^-324 ~ <1）

>>>>
0000 0000 0000 0000 0000 0000 0000 0000
0000 0000 0000 0000 0000 0000 0000 0001 
~
1000 0000 0000 0000 0000 0000 0000 0000 
0000 0000 0000 0000 0000 0000 0000 0001

已经证明过

为什么0.1 + 0.2 不等于 0.3？

我们先把0.1 和 0.2 转化为2进制

function f3(n){
    let str = '0.';
    let num = n * 10 ;
    for(var i = 0;i<100;i++){
        num *= 2
        if(num >= 10){
            str += 1
            if (num === 10) break
            num -= 10
        }else{
            str += 0
        }
    }
    return str + Array(100 - i).fill(0).join('')
 }

很明显，0.1 和 0.2 都无法用2进制精准表示，呈现出的是无限循环。

我们看一个实例，来看看IEEE如何做舍入处理的
（例子是IEEE754单精度浮点格式（32 位），没找到64位的，自己懒得算了。。不过可以说明问题）

JS基础知识回顾-数值-IEEE754

1.数组

2.位运算符

带号右移位运算符（>>）

3.数字计算

IEEE754

问题1：定点表示中，只有两个相关硬件，整数定点机，和小数定点机。一条数据，要么表示整数，要么就表示小数。

根据上述操作，我们解决了整数，小数共存的二进制编码的问题。

问题4：对于类似+(-)0.000001的真值要保存过多的0，浪费存储空间，且降低精度。

那么其实，问题2，3也解决了

但是！

那他到底拿这两个特殊指数干啥了呢？

先说全指数位全1（称为：特殊数值）

再说指数位全0（称为：非格式化数值）

js能精确计算的数值范围是 -2⁵³ ~ 2⁵³

js能表示的纯整数数值范围是 -1.8x10³⁰⁸ ~ 1.8x10³⁰⁸

js能表示的纯小数数值范围是（-1< ~ -5x10^-324）和（5x10^-324 ~ <1）

为什么0.1 + 0.2 不等于 0.3？

你可能感兴趣的:(JS基础知识回顾-数值-IEEE754)

JS基础知识回顾-数值-IEEE754

1.数组

2.位运算符

带号右移位运算符（>>）

3.数字计算

IEEE754

问题1：定点表示中，只有两个相关硬件，整数定点机，和小数定点机。一条数据，要么表示整数，要么就表示小数。

根据上述操作，我们解决了整数，小数共存的二进制编码的问题。

问题4：对于类似+(-)0.000001的真值要保存过多的0，浪费存储空间，且降低精度。

那么其实，问题2，3也解决了

但是！

那他到底拿这两个特殊指数干啥了呢？

先说全指数位全1（称为：特殊数值）

再说指数位全0（称为：非格式化数值）

js能精确计算的数值范围是 -253 ~ 253

js能表示的纯整数数值范围是 -1.8x10308 ~ 1.8x10308

js能表示的纯小数数值范围是 （-1< ~ -5x10-324）和（5x10-324 ~ <1）

为什么0.1 + 0.2 不等于 0.3？

你可能感兴趣的:(JS基础知识回顾-数值-IEEE754)

js能精确计算的数值范围是 -2⁵³ ~ 2⁵³

js能表示的纯整数数值范围是 -1.8x10³⁰⁸ ~ 1.8x10³⁰⁸

js能表示的纯小数数值范围是（-1< ~ -5x10^-324）和（5x10^-324 ~ <1）