R语言与回归分析学习笔记(应用回归小结)(2)
三、异常点
所谓的异常点一般指有着很大残差(绝对值)的点,如果对模型的参数估计值影响出现了比例失衡,那么我们称之为强影响点。为了说明异常点与强影响点的判别,我们特意采用模拟的数据来证实它。
为了简单起见,我们采用一元模型来说明问题。
模拟数据:(模型:y=0.5+1.7*x+e)
x<-rexp(100,0.2)
e<-rnorm(100)
y<-0.5+1.7*x+e我们来看看这个回归结果
lm(y~x)输出结果:
Call:
lm(formula= y ~ x)
Coefficients:
(Intercept) x
0.5489 1.7955
我们来改变其中的一个点:
y[50]<-0.7+0.2*x[50]+e[50]那么他是异常点吗?这个改变毕竟不大,能被观测出来吗?我们可以先看看回归系数发生了什么样的改变?
lm.reg1<-lm(y~x)
lm.reg1Call:
lm(formula= y ~ x)
Coefficients:
(Intercept) x
0.3827 1.7404
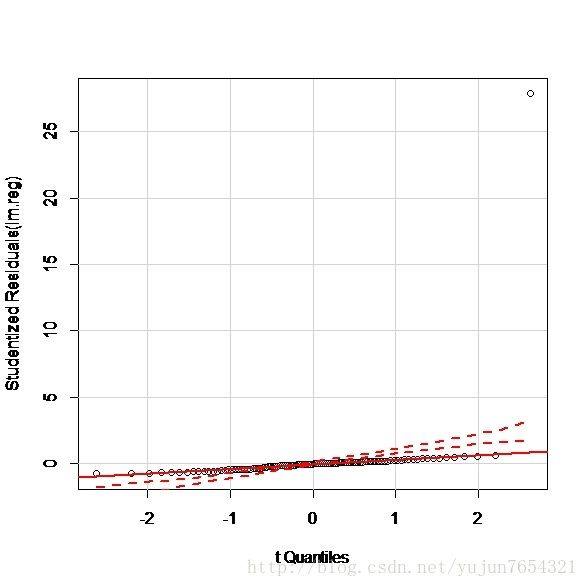
我们通过qq图进行初步判断:
显然初步判断它没有成为一个异常点。我们也可以通过car包里的outlierTest()来判断。
outlierTest(lm.reg1)输出结果:
NoStudentized residuals with Bonferonni p < 0.05
Largest|rstudent|:
rstudent unadjusted p-value Bonferonni p
36 2.285984 0.024431 NA
也就是说没有异常点,其中残差最大的点是36号点。这也告诉我们不是所有的不合模型的偏差都会归结为异常点。
我们来制造一个异常点且为强影响点并且运用outliertest()分析它。
y[100]<-3+5.8*x[100]+2*e[100]
lm.reg<-lm(y~x)
outlierTest(lm.reg)rstudent unadjusted p-value Bonferonni p
100 27.85628 4.4912e-48 4.4912e-46
我们还是可以通过qq图来直视这个结果:
100号点实在太明显了。
接下来,我们来讨论100号点是否为强影响点?我们先看回归模型:
lm.regCall:
lm(formula= y ~ x)
Coefficients:
(Intercept) x
0.6027 1.7503
截距项变化明显,那么它是强影响点无疑。但是我们不知道真实模型呢?我们使用cook距离来判断。一般来说cook距离大于4/(n-k-1),则表明其为强影响点,其中n为观测数,k为变量数。
在R中输入命令:
cooks.distance(lm.reg)可以得到cook距离,在输入:
result<-cooks.distance(lm.reg)
result[cooks.distance(lm.reg)>4/(100-1-1)]输出结果:
100
0.4524937
可以发现只有100号点为强影响点。作图来看:
(绘图代码:
cook<-4/(100-1-1)
plot(lm.reg,which=4,cook.levels=cook)
abline(h=cook,lty=2,col=2))
我们还可以使用influencePlot()将异常点绘入图中:
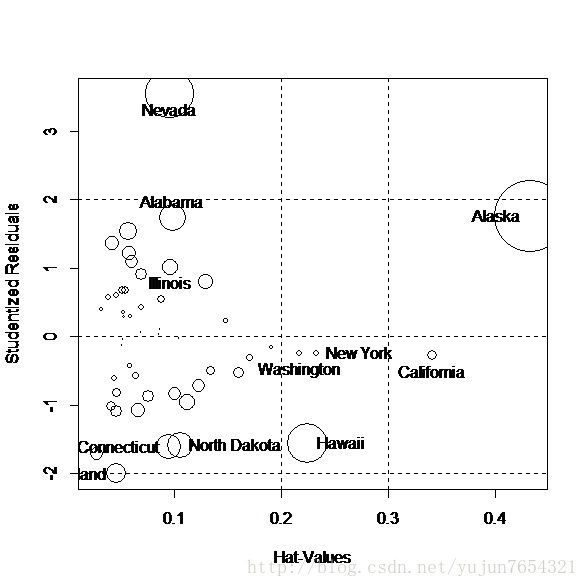
influencePlot(lm.reg)
上图为影响图。纵坐标超过+2或小于-2可认为是异常点,水平轴超过0.2或0.3有高杠杆值,圆圈越大的点越可能是强影响点。
图中有标号的数据为:
StudRes Hat CookD
47 -0.4933677 0.04839400 0.07897794
53 0.1907168 0.09983013 0.04513239
64 -0.7393266 0.02657122 0.08657289
71 -0.4238429 0.14366355 0.12327255
98 0.4161791 0.04972515 0.06760339
100 27.8562847 0.01028211 0.67267654
我们最后以state数据来做一幅影响图(续二中的例子)来判断二中的结论是否正确。
四、回归模型的改进
对于强影响点我们的处理异常的简单,在回归时去掉它。但是我们必须注意的是对于异常点除非记录有误外都应当仔细对待,认真分析原因。记住:我们最伟大的进步一般都源于异于先验认知的东西。在计量中这点尤为重要。
对于复共线性,我们一般采用岭回归或主成分回归来解决它。
对于异方差性,我们可以使用box-cox变换来处理它。
这两个的具体例子分别参见《回归分析作业2》、《回归分析作业3》。在《R in action》一书中还提及了car包中的三个函数powerTransform(),boxTidwell(),spreadLevelPlot()来改善线性性与异方差性。我们还是以作业3中的例子来运用这几个函数。
library(xlsx)
workbook<-"D:/R/data/3-15.xlsx"
mydataframe<-read.xlsx(workbook,1)
lm.reg2<-lm(Y~X,data=mydataframe)
spreadLevelPlot(lm.reg2)输出结果:
Suggested power transformation: 0.3641616
说明异方差性还是明显的。
在R中输入以下代码:
library(xlsx)
workbook<-"D:/R/data/3-15.xlsx"
mydataframe<-read.xlsx(workbook,1)
lm.reg2<-lm(Y~X,data=mydataframe)
spreadLevelPlot(lm.reg2)
library(MASS)
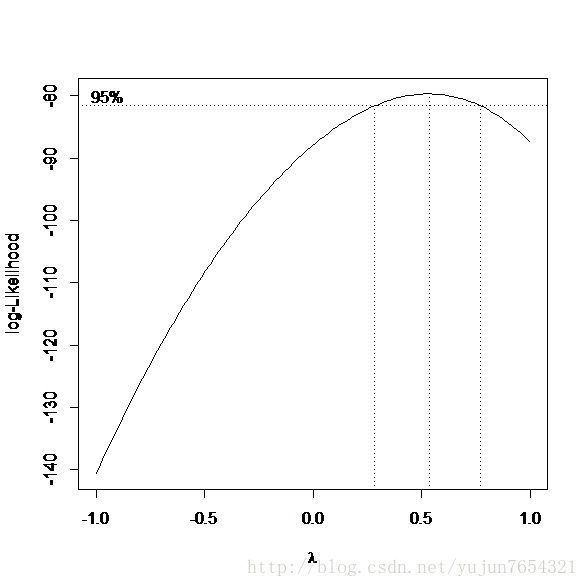
boxcox(lm.reg2,lambda= seq(-1, 1, length = 50))
which.max(box$y)
box$x[77]
summary(powerTransform(mydataframe$Y))
boxTidwell(Y~X,data=mydataframe)输出结果:
>which.max(box$y)
[1] 77
>box$x[77]
[1] 0.5353535
>summary(powerTransform(mydataframe$Y))
bcPowerTransformation to Normality
Est.Power Std.Err. Wald Lower Bound Wald Upper Bound
mydataframe$Y 0.2773 0.1399 0.003 0.5516
Likelihoodratio tests about transformation parameters
LRT df pval
LR test,lambda = (0) 3.942405 1 4.708342e-02
LR test,lambda = (1) 25.999924 1 3.414308e-07
>boxTidwell(Y~X,data=mydataframe)
Score Statistic p-value MLE of lambda
1.529055 0.1262507 1.517633
iterations = 4
这里三个变换得到的结果并不一致,powerTransform()给出的变幻是u=y^0.2773,boxcox()给出的变换是u=y^ 0.5353535,,boxTidwell()认为将x变换为z=x^1.517633线性性会有很好的改善。但是我们观察boxcox给出的图我们也很清楚的看到这三个结果都是可接受的,最后得到的结果都可以使得线性性极大地提高。至于选择哪一个,我们得从数据本身出发来通过舍入得到答案。还有变量除了幂次变换,logit变换,对数变换都是常用的。
最后提醒一下,谨慎对待变量变换,毕竟我们的回归并不一定以提高R^2为目的,特别是在经济学中。
引用《R in action》中的一段话来作为本节的结束:
The decision regarding when to try to improve the fit of an OLS regression model and when to try a different approach, is a complex one. It’s typically based on knowledge of the subject matter and an assessment of which approach will provide the best result.
五、回归的变量选择
变量选择是个非常有意思的话题,岭回归,lasso都是在变量选择上可以使用的方法,我们今天不提他们,仅介绍《线性统计模型》一书中提到的两种方法:逐步回归与全子集回归。例子参见《回归分析作业4》
我们只补充介绍car包中的subsets()函数。其调用格式为:
subsets(object,
names=abbreviate(object$xnames, minlength = abbrev),
abbrev=1, min.size=1, max.size=length(names), legend,
statistic=c("bic", "cp", "adjr2","rsq", "rss"),
las=par('las'), cex.subsets=1, ...)
它支持各种准则的子集回归判断。比逐步回归的step函数要好一些。大部分情况下,全子集回归要优于逐步回归,但是大量预测变量时他会变得很慢。