建议收藏:彻底弄懂常见的几种概率分布
常见的几种概率分布
1 二项分布
所谓的二项式分布就是只有两个可能结果的分布,例如:阴和阳、成功和失败、得到和丢失等,每一次尝试成功或失败的概率相等。如果在实验中成功的概率为0.9,则失败的概率可以很容易地计算得到 q = 1 - 0.9 = 0.1。每一次尝试都是独立的,前一次的结果不能决定或影响当前的结果。将只有两种结果的独立实验重复N次,得到的概率分布叫做二项分布,对应的实验叫做N重伯努利实验。N重伯努利实验的参数是N和p,其中N是试验的总数,p是每次试验成功的概率,其数学公式如下:
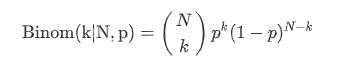
二项分布的期望为N·p,方差为N·p·q,其中(q=1-p)。为了更好的建立概率和概率分布之间的关系,引入了概率质量函数(PMF)和概率密度函数(PDF)。
概率质量函数是对离散随机变量的定义,它描述的是离散随机变量在各个特定取值的概率,通俗来说,就是对于一个离散型概率事件来说, 使用这个函数来求它解的各个事件的概率。概率密度函数是对连续性随机变量的定义,与PMF不同的是 PDF 在特定点上的值并不是该点的概率, 连续随机概率事件只能通过对这段区间进行积分,来求解一段区域内发生事件的概率。对于PMF和PDF,使用CDF(累积分布函数)计算在某一区间或集合内累积分布的概率。
接下来使用scipy提供的统计模块,模拟抛掷10次硬币的伯努利实验所对应的PMF质量分布函数和CDF累积分布函数,并使用matplotlib进行可视化 :
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
plt.bar(x=np.arange(10),height=(stats.binom.pmf(np.arange(10), p=.5, n=10)), color="#008fd5")# PMP概率质量函数
# CDF累积分布函数
plt.plot(np.arange(10),stats.binom.cdf(np.arange(10), p=.5, n=10), color="#fc4f30")
plt.show()
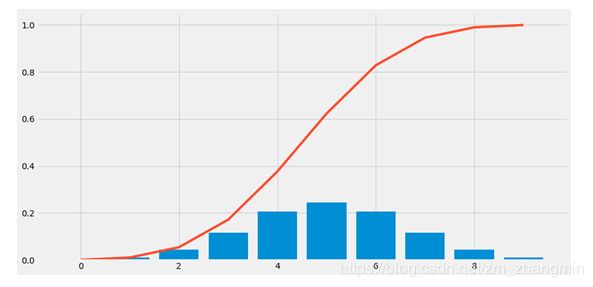
红色的线条是CDF累积分布函数,蓝色的柱条表示投掷产生期望结果次数的概率。可以看到CDF是PMF的累积。当p=0.5时,PMF左右对称,当p大于或小于0.5时,将出现“长尾”;N越大,PMF图像越扁平。
2 正态分布
宇宙中大多数现象的概率呈现正态分布,大量的随机变量被证明是正态分布的。随机变量X服从数学期望为μ、方差为 sigma^2的正态分布 ,记为:
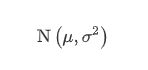
其概率密度函数定义为 :
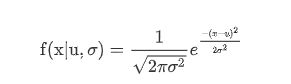
期望值μ决定了分布的位置,其标准差σ决定了分布的幅度。当μ= 0,σ=1时的正态分布是标准正态分布。一般正态分布可通过下面公式转换为标准正态分布。
若:
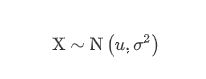
令:
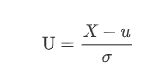
则:
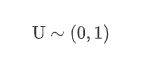
接下来用scipy模块绘制出正态分布的PDF和CDF图像 :
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
datas = np.linspace(-4, 4, 100)
plt.plot(datas, stats.norm.pdf(datas))
plt.plot(datas, stats.norm.cdf(datas))
plt.show()
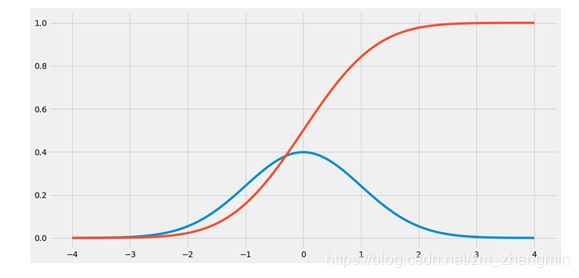
对于正态分布,概率密度函数PDF关于均值对称,且标准差越小,图像越“尖”,分布越集中。
3 均匀分布
对于投骰子来说,结果是1到6,并且得到任何一个结果的概率是相等的,这就是均匀分布的基础。与伯努利分布不同,均匀分布的所有可能结果是相等的。如果变量X是均匀分布的,则密度函数可以表示为 :
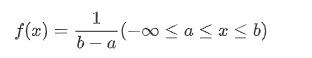
均匀分布的概率密度曲线如下所示:
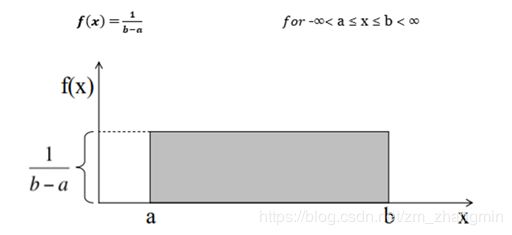
函数图像有a和b值确定,在scapy模块中的uniform函数中通过loc和scale关键字参数控制。下面是均匀分布的PDF和CDF函数图像和代码:
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
plt.figure(figsize=(15,8))
datas = np.linspace(-8, 8, 100)
# PDF loc=0, scale=1
plt.plot(datas, stats.uniform.pdf(datas,loc=0, scale=1))
plt.fill_between(datas,stats.uniform.pdf(datas,loc=0, scale=1))
# PDF loc=-3, scale=3
plt.plot(datas, stats.uniform.pdf(datas, loc=-3, scale=3))
plt.fill_between(datas,stats.uniform.pdf(datas,loc=-3, scale=3))
plt.show()
4 泊松分布
现实生活中,很多现象服从泊松分布,某种程度上泊松分布可用于近似计算二项分布。下面是生活中服从泊松分布的例子:
(1)医院在一天内接到的紧急电话的数量。
(2)某个地区在一天内报告的失窃的数量。
(3)在一小时内抵达沙龙的客户人数。
(4)在特定城市上报的自杀人数。
(5)书中每一页打印错误的数量。 泊松分布适用于在随机时间和空间上发生事件的情况。
我们只关注事件在某一段时间内发生的次数,泊松分布中使用了这些符号 :
(1) lambda:事件发生的速率
(2) t:时间间隔
(3) X:该时间间隔内发生的事件数。
其中,X称为泊松随机变量,X的概率分布称为泊松分布。令μ表示长度为t的间隔中的平均事件数。那么 :
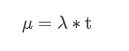
一个事件要服从泊松分布,需要符合以下条件:
(1)将该时间段无限分隔成若干个小的时间段,在这个接近于零的小时间段里,该事件发生一次的概率与这个极小时间段的长度成正比。
(2)在每一个极小时间段内,该事件发生两次及以上的概率恒等于零。
(3)该事件在不同的小时间段里,发生与否相互独立。
如果事件满足上述三个条件,则该事件称为Poisson Process。泊松分布的数学描述如下:
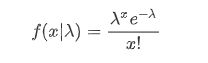
式中的lambda表示分布的期望值。例如已知医院平均每个小时接到紧急电话的次数为3,请问接下来两个小时,接收到紧急电话的个数?有可能接到20个,也有可能一个都没有,这是无法知道的。泊松分布就是描述某段时间内,事件具体的发生概率。用泊松分布对该事件建模,计算公式如下:
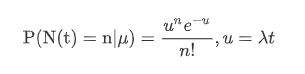
N表示某种函数关系,t表示事件,u表示该段时间内事件发生的平均值,等于发生速率和时间的乘积 ,n表示该段时间内事件发生的次数。
接下来两个小时,一次都不发生的概率为:

接下来两个小时,至少发生2次的概率为:
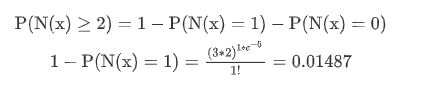
所以:
![]()
接下来使用scipy库实验下泊松分布并绘制出函数图像。
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
plt.figure(figsize=(15,8))
# PDF LAM = 1
plt.scatter(np.arange(20),stats.poisson.pmf(np.arange(20), mu=1),s=100)
plt.plot(np.arange(20),stats.poisson.pmf(np.arange(20), mu=1))
# PDF LAM = 5
plt.scatter(np.arange(20),stats.poisson.pmf(np.arange(20), mu=5),s=100)
plt.plot(np.arange(20),stats.poisson.pmf(np.arange(20), mu=5))
# PDF LAM = 10
plt.scatter(np.arange(20),stats.poisson.pmf(np.arange(20), mu=10))
plt.plot(np.arange(20),stats.poisson.pmf(np.arange(20), mu=10))
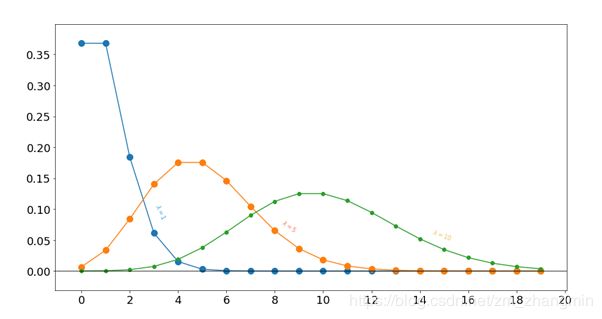
从函数图像中可以明显看出,lambda值越小,函数图像越“尖”, lambda 值越大,函数图像越扁平。在lambda值附近,PMF概率质量函数取得最大值。
5 卡方分布
若n个相互独立的随机变量 :

服从标准正态分布,则这n个服从标准正态分布的随机变量的平方和 Q:

构成一个新的随机变量,该随机变量的分布规律称为
![]()
卡方分布(Chi-Square Distribution)。卡方分布的参数是u自由度,记作 :
![]()
其中u=n-k,k为限制条件数。卡方分布是由正态分布构造而成的一个新的分布,当自由度u很大时,X^2分布近似为正态分布。数学表达式入下 :
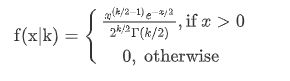
其中k代表自由度 ,
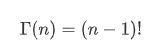
它是一个gamma函数,是整数k的封闭形式。卡方检验的基本思想就是观察并检验统计样本的实际观测值与理论推断值之间的偏离程度,实际观测值与理论推断值之间的偏离程度就决定卡方值的大小,卡方值越大,越不符合;卡方值越小,偏差越小,越趋于符合,若两个值完全相等时,卡方值就为0,表明理论值完全符合。接下来借助scipy模块绘制卡方分布在不同自由度下的概率密度函数图像 。
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
plt.figure(figsize=(15,8))
datas = np.linspace(0, 20, 100)
# PDF
plt.fill_between(datas,stats.chi2.pdf(datas, df=5),hatch="/")
plt.fill_between(datas,stats.chi2.pdf(datas, df=8),hatch="*")
plt.fill_between(datas,stats.chi2.pdf(datas, df=10),hatch="+")
plt.fill_between(datas,stats.chi2.pdf(datas, df=15),hatch="//")
plt.show()
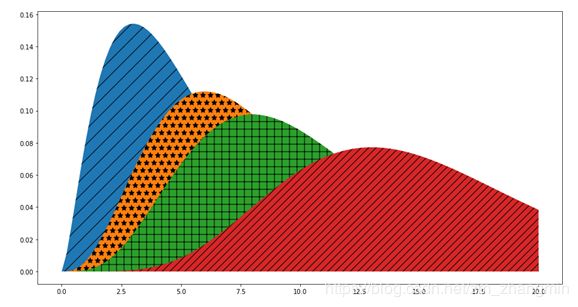
由函数图像可知,卡方分布自由度越大,越“扁平”,越接近于正态分布。卡方分布经常应用于卡方检验中,被誉为二十世纪科学技术所有分支中的20大发明之一。
6 Beta分布
Beta分布可以看作一个概率的概率分布,当你不知道一个东西的具体概率是多少时,它可以给出了所有概率出现的可能性大小。
举一个简单的例子,熟悉棒球运动的都知道有一个指标就是棒球击球率(Batting Average),就是用一个运动员击中的球数除以击球的总数,我们一般认为0.266是正常水平的击球率,而如果击球率高达0.3就被认为是非常优秀的。现在有一个棒球运动员,我们希望能够预测他在这一赛季中的棒球击球率是多少。你可能就会直接计算棒球击球率,用击中的数除以击球数,但是如果这个棒球运动员只打了一次,而且还命中了,那么他就击球率就是100%了,这显然是不合理的,因为根据棒球的历史信息,我们知道这个击球率应该是0.215到0.36之间才对啊。
对于这个问题一个最好的方法就是用Beta分布,这表示在我们没有看到这个运动员打球之前,我们就有了一个大概的范围。Beta分布的定义域是(0,1)这就跟概率的范围是一样的。接下来我们将这些先验信息转换为Beta分布的参数,我们知道一个击球率应该是平均0.27左右,而他的范围是0.21到0.35,那么根据这个信息,我们可以取 (击中了99次,未击中186次)。
Beta分布的数学描述如下:
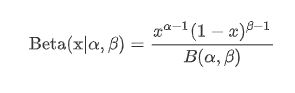
其中:

alpha和beta可以看作是历史经验总结的成功和失败的次数。对于棒球运动员, alpha和beta可以是该运动员历史信息所统计得出的成功和失败的次数,当某一棒击中时 ,alpha=alpha+1对结果影响不大,可作为击中概率的估计。接下来借助scipy模块对Beta分布不同取值情况下的函数图像进行可视化 .
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
plt.figure(figsize=(15,8))
datas = np.linspace(0, 1, 200)
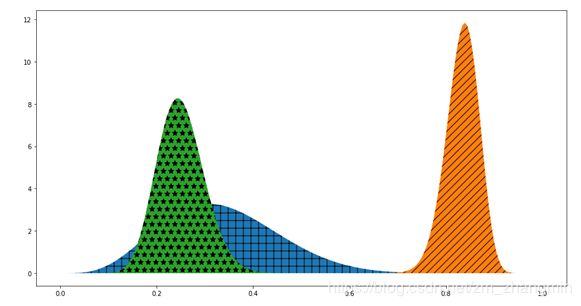
plt.fill_between(datas,stats.beta.pdf(datas, a=5, b=10),hatch="+")
plt.fill_between(datas,stats.beta.pdf(datas, a=100, b=20),hatch="//")
plt.fill_between(datas,stats.beta.pdf(datas, a=20, b=60),hatch="*")
plt.show()