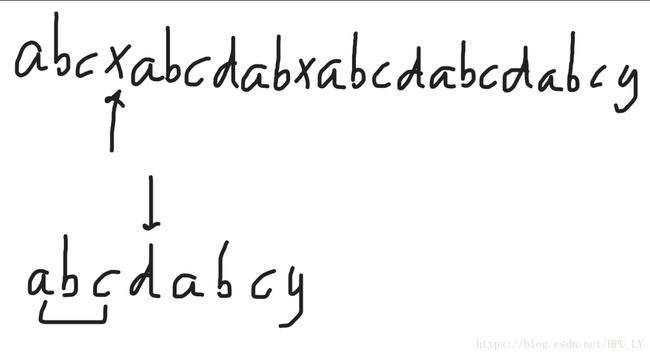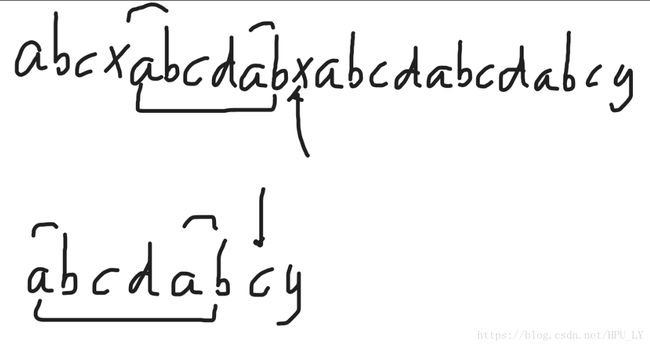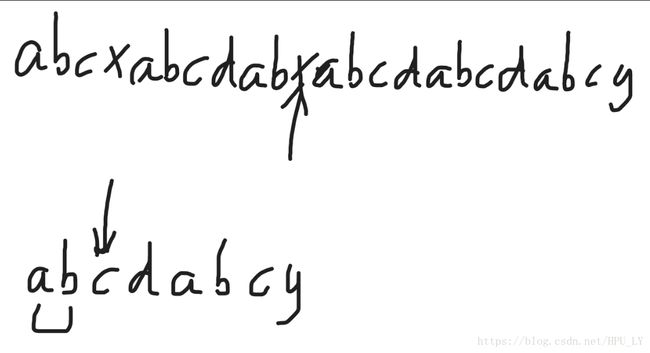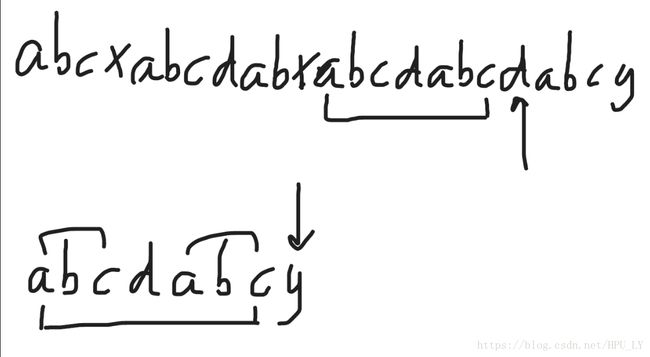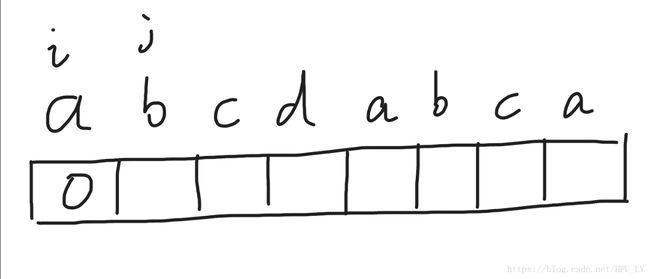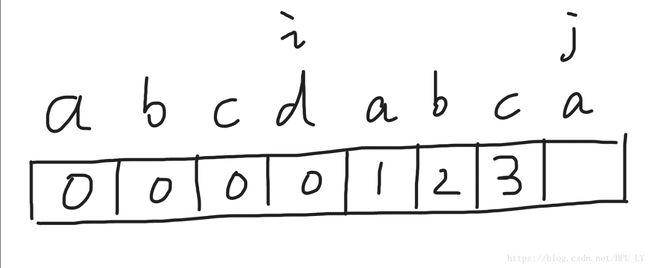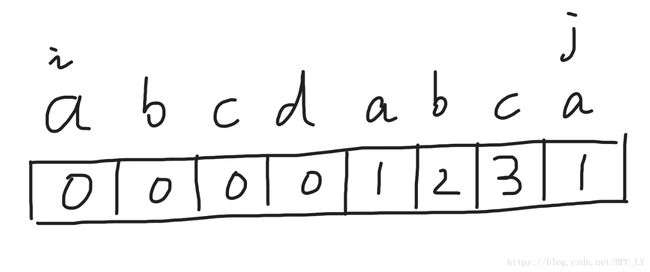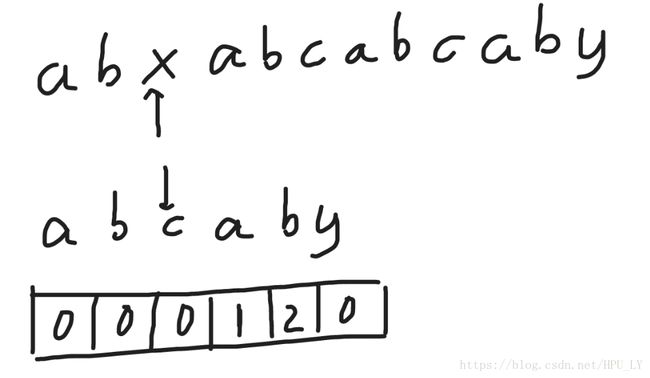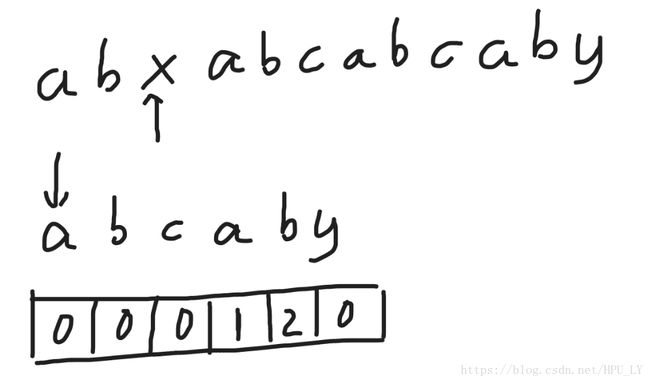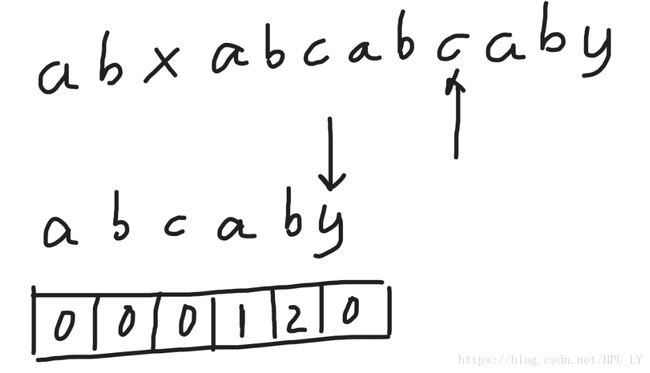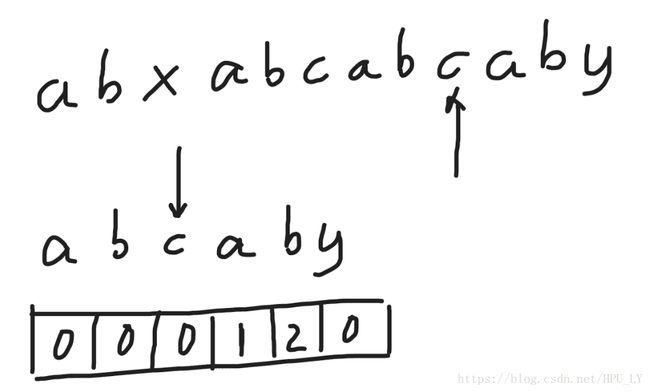KMP算法——基于Youtube外国小哥讲解及其Github上代码的理解

前言

本篇文章是在看了CSDN上那些“大佬”们对KMP算法的长篇大论后仍然看不懂，而在Youtube上看了一外国小哥讲解的视频后有所领悟，同时想给广大受苦群众分享外国小哥的讲解而写的文章。

视频源地址https://www.youtube.com/watch?v=GTJr8OvyEVQ

Bilibili搬运附中英字幕https://www.bilibili.com/video/av3246487?from=search&seid=4416876704360741053

外国小哥的Github主页http://github.com/mission-peace/interview/wiki

外国小哥关于KMP算法的Java模板

https://github.com/mission-peace/interview/blob/master/src/com/interview/string/SubstringSearch.java

各位可以直接浏览以上网页去获取直接信息，跳过我写的文章，因为这篇文章主要是把原作者的视频转换成文本。

如果您不想看视频，那么您就可以看看这篇文章，不过我也不建议您这么做，因为从原作者获取信息是最直接的，通过他人获取的原作者的信息也许就变了味儿。

因本人能力有限，不保证文章质量，抱歉！

---

正文

普通暴力的字符串查询搜索方法

要求是在母串中找到子串，如果找到返回母串所对应子串首字母的下标，如果找不到返回-1等。

 

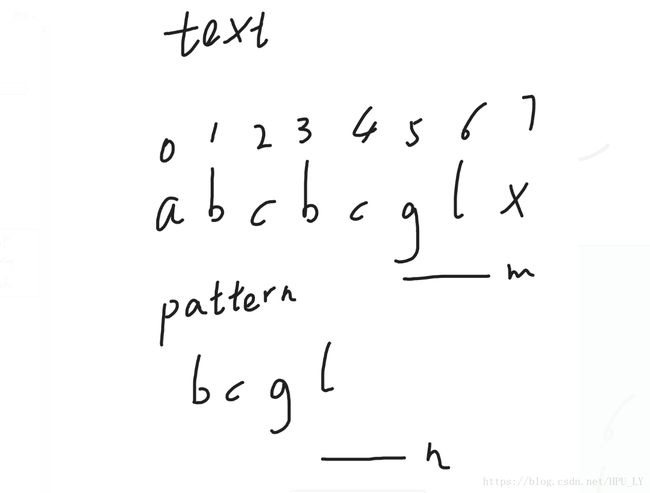
如上图所示，text代表母串“abcbcglx”，pattern代表子串“bcgl”，下面人工简单模拟一下暴力算法。

首先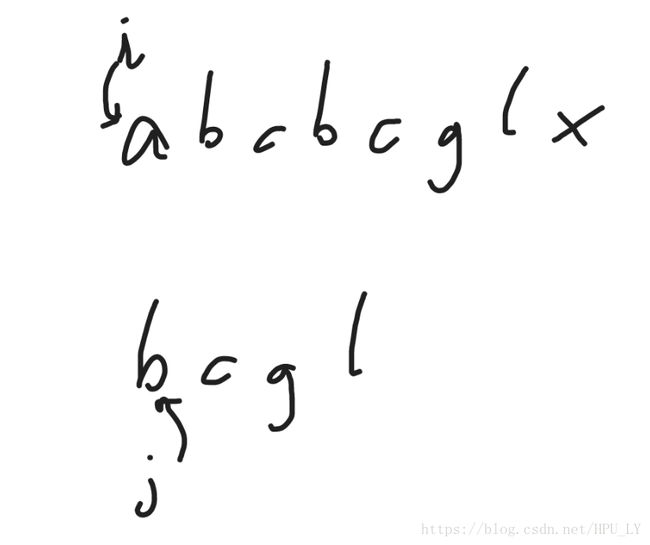定义i，j在text以及pattern的首字母上，然后依次往后匹配。

1、a与b不匹配，i++往后走一位。

2、b与b匹配，i++，j++各往后走一位。

3、c与c匹配，i++，j++各往后走一位。

4、b与g不匹配，i回到匹配开始位置（b）的后一位（c），j回到子串的首字母。

......

以此类推。

时间复杂度

假如母串是“abcabcabcabcabcabcabc...abx”，子串是“abx”，这样每次母串到c的时候与子串的x不匹配，i往后走，j又回到子串首字母，这样循环下去最差的时间复杂度为O(m*n），m、n是母、子串的长度。毋庸置疑，当字符串长度很长的时候，时间复杂度还是相当高的。

KMP算法

KMP算法是一种改进的算法，由D.E.Knuth，J.H.Morris和V.R.Pratt同时发现，因此人们称它为KMP算法。KMP算法的关键是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。

演示

如上图所示，母串“abcxabcdabxabcdabcdabcy”，子串“abcdabcy”。

 

开始的匹配方法与暴力匹配一致。

如上图所示，母串的x与子串的d不匹配，KMP算法不是让i回到匹配开始的位置，j回到子串开始的位置，这时要看子串匹配失败处前面的字符串“abc”有没有相同的前缀和后缀（字符串前后缀问题这里不解释，不会的读者自行百度），这里并不存在前后缀，所以i不动，j回到子串开始，随后会再进一步理解这个例子，读者不要着急。

 

如上图所示，经历了第一次匹配失败后，i和j分别来到了x和c。在子串中，c前面的字符串为“abcdab”，即相同前后缀“ab”，这就表示在母串中同样有一段字符串“abcdab”，这就意味着，子串中c前面的字符串的前缀与母串中x前面的字符串的后缀所匹配，不用再进行比较，i原地不动，j回到前缀“ab”后的c。如果采用暴力算法，i回到匹配开始的后一位b，j回到子串开始，发现都不匹配，直到子串的a和母串的a匹配，也就是子串的前缀匹配到母串的后缀，KMP算法省时间就体现在这里。

如上图所示，x与c不匹配，c前面的字符串“ab”也没有相同前后缀，i不动，j回到子串的开始。

a与x不匹配，i++往后走一位。

如上图所示，d和y不匹配后，y前面的字符串“abcdabc”有相同的前后缀“abc”，所以d前面字符串也有同样的字符串，这样无需比较母串中的后缀和子串中的前缀，j回到“abc”后面的d即可，这时发现从d开始后面的字符一一匹配，至此子串在母串的位置被找到了。

---

那么现在的问题就是，如何找子串中相同的前后缀呢？并且用什么样的数据结构把前后缀信息给保存下来？接下来我们继续。

这里有一子串“abcdabca”,我们用一个nxt数组来保存前后缀信息，定义i在开始位置，j在第二个位置。

a与b不匹配，nxt[j]=0，j++往后走一位，c与a也不匹配，nxt[j]=0，j++再往后走一位，以此类推。

直到j走到a，a与a匹配，nxt[j]的值是i的值+1，此时i在开始位置，下标为0，所以nxt[j]=0+1=1，表示字符串从开始到j这个位置，存在最长公共前后缀的长度为1，然后i，j分别往后各走一位。b与b匹配，nxt[j]=1+1=2，i、j分别往后再走一位，以此类推。

i来到了d，j来到了a，d与a不匹配，i要回到i-1所对应的nxt[i-1]的值（下一个例子会进一步解释这个原因）。这里i-1是c，nxt数组保存的值是0，i就要回到0这个位置，

这时a与a匹配，nxt[j]=0+1=1。

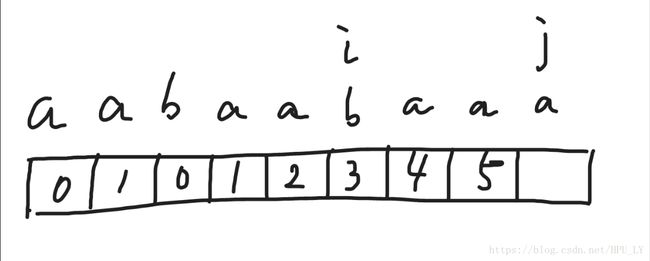
下一个例子，字符串“aabaabaaa”，首先按照之前的思路把各自所对应的nxt数组的值填好，我们直接来看当i来到b，j来到a

b与a不匹配的时候，是如何处理的。

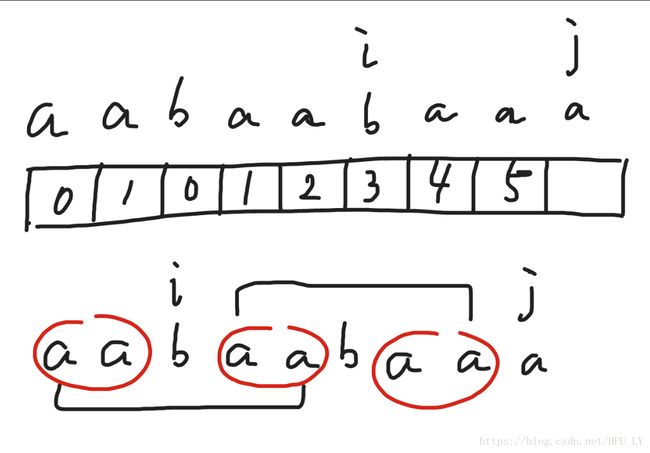
正如前面所说，i要回到i-1所对应的nxt[i-1]的值，这里i-1对应的值是2，所以i要回到2这个位置

 

 

 

i-1所对应的nxt[i-1]的值表示i前面的字符串的最长公共前后缀长度是多少，回到nxt[i-1]也就是回到i前面字符串最长公共前缀的后一位，因为i前面的字符串与j前面的字符串拥有相同的最长公共前后缀，也就是说i前面字符串的最长公共后缀与j前面字符串的最长公共前缀相同，所以i只需回到i前面字符串最长公共前缀的后一位开始比较。

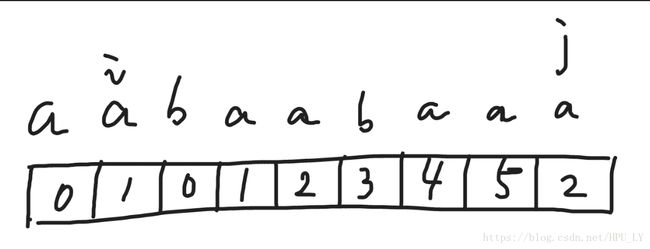
最终nxt数组的结果如上图所示。

代码实现

void getnxt(){
	int i=0,j=1;//两个指针
	nxt[0]=0;//初始化
	while(j

接下来我们将看看这样一个nxt数组在KMP算法中到底起什么样的作用 

---

如图所示，母串“abxabcabcaby”，子串“abcaby”，子串对应的nxt数组同时也给出了，下面我们手动模拟一遍KMP算法。
定义i、j分别位于母子串的起始位置，如果匹配，i、j各往后一位。这时如图所示，i到x，j到c，x与c不匹配，j要回到j-1所在的nxt数组的值，这里是0，所以j=0。

x与a不匹配，由于j在起始位置，所以i往后走一位，接着开始匹配。

直到，i到c，j到y，c与y不匹配，j要回到j-1所在的nxt数组的值，这里是2，j=2，接着进行匹配。

随后发现，母子串一一匹配，子串在母串中的位置被找到。

代码实现

void KMP(){
	int i=0,j=0;//初始化
	while(i

时间复杂度

O（n+m）

这里暂时没想明白，在以后的更新中会再说明。