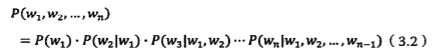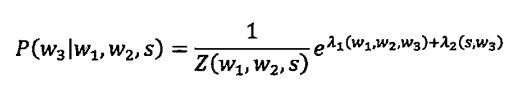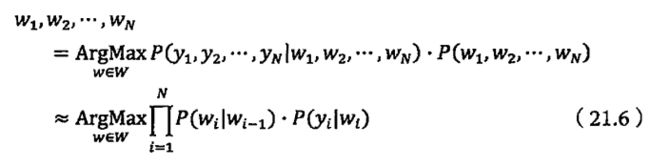《数学之美》读书笔记
看了吴军的《数学之美》,感触颇多。吴军先生能通过简单的故事和诙谐的语言,将晦涩难懂的数学原理解释清楚,让人再次感受到数学的博大精深。读了这本书之后,发现曾经只和成绩挂钩的数学原理还能这么玩,这么接地气。为此,摒弃应试的动机,下一步计划重学一遍概率论、线代、高数等数学,以提高自己。本文是个人读《数学之美》记录下阅读时的最直接的感受,希望后期能适时翻阅,思想上和知识层面上共同指导自己。
第二版前言
今天,除了初等数学(加减乘除),大家对数学,尤其是纯粹的数学用途产生了怀疑。很多大学所学的数学,可能一辈子都没有机会应用,几年后就差不多忘光了。原因:----因为不懂得数学的应用就在我们生活中,没感受到数学之美,数学也就真的白学了。
要了解世界级学者他们的平凡和卓越,理解他们取得成功的原因,感受那些真正懂得数学之美的人们所拥有的美好人生。
第1章 文字和语言VS数字和信息
文字只是信息的载体,而非信息本身。
罗塞塔3份文本的数据保存形式,为自然语言处理提供两点指导:
- 信息冗余是信息安全的保障
- 语言的数据,称为语料。尤其在翻译中,语料的对比,是从事机器翻译的基础。
古时候的文言文和白话文,其实就是类似于今天信道压缩与否的区别,比如书中
第2章 自然语言处理从规则到统计
从规则到统计的过渡过程,是在很长的历史内完成的。
基于统计的方法的核心模型是通信系统加隐含马尔可夫模型。统计模型的思想,可充分发挥数据的优势,大大提高效果。
第3章 统计语言模型
统计模型的核心思想是 马尔可夫模型(当前状态只和前面的一个或多个状态有关)
而这个,可以用样本的统计方法,近似估计各种条件概率。这期间,需要进行模型的训练和零概率问题的平滑处理。
模型的训练
平滑处理
训练参数的一个直接的办法是增加数据量,但是仍然会遇到零概率事件。我们本这种模型称为“不平滑”,必须解决。
古德-图灵估计
语料选取的问题
如果训练语料和模型应用的领域脱节,那么模型的效果将大打折扣。
训练数据通常越多越好,虽然通过平滑过渡可以解决平滑问题。但是,片面追求大规模数据,是没有意义的。
训练语料的噪声高低或多或少会对模型效果产生影响。在训练之前,有时需要对训练的数据进行预处理。一般,少量的随机噪声清除的成本比较高,通常不处理。但是大量的噪声,还是有必要进行处理的,而且他们也比较号处理,比如网页中的大量制表符。
第4章 谈谈分词
分词的二义性问题是语言歧义性的一部分,郭进博士用统计语言模型成功解决分词二义性问题,将汉语分词的错误率降低了一个数量级。
最好的分词方法,应该保证分完词后的这个句子出现的概率最大。统计语言模型可以算出这个句子出现的概率。统计语言可以计算出每种分词后句子出现的概率。(马尔可夫)
分词,我们可以把它看成是一个动态规划(Dynamic Programming) 的问题,并利用 “维特比”(Viterbi) 算法快速地找到最佳分词。
一般来讲,根据不同应用,汉语分词的颗粒度大小应该不同。比如,在机器翻译中,颗粒度应该大一些,“北京大学”就不能被分成两个词,这样效果会更好些。而在语音识别中,“北京大学”一般是被分成两个词。比如网页搜索中,小的粒度比大的粒度效果更好。因此,不同的应用,应该有不同的分词系统。
中文分词是一个已经解决的问题,提升的空间是微乎其微的。只要使用统计模型,效果就差不到哪去。英文等西方语言,本身就没有分词问题,除非要做文本分析找词组。
第5章 隐含马尔可夫模型
为什么用到马尔可夫
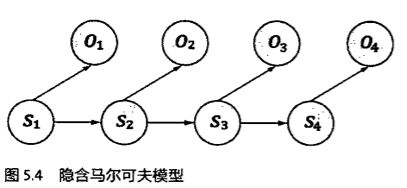
自然语言处理其实和通信的过程一样,都涉及到对信息的编码发送与接收解码的过程。 其中 s1,s2,s3...表示信息源发出的信号。o1, o2, o3 ... 是接受器接收到的信号。通信中的解码就是根据接收到的信号 o1, o2, o3 ...还原出发送的信号 s1,s2,s3...。以语音识别为例,当我们观测到语音信号 o1,o2,o3 时,我们要根据这组信号推测出发送的句子 s1,s2,s3。用统计学来描述,就是在已知 o1,o2,o3,...的情况下,求使得条件概率P (s1,s2,s3,...|o1,o2,o3....) 达到最大值的那个句子 s1,s2,s3,...
根据贝叶斯公式,有
![]()
一旦 o1,o2,o3,...产生了,那么P (o1,o2,o3....)也就是一个可以忽略的常量。上式转换成公式求
ArgMax( P(o1,o2,o3,...|s1,s2,s3....) * P(s1,s2,s3,...) )。
什么是马尔可夫
- s1,s2,s3,... 是一个马尔可夫链,也就是说,si 只由 si-1 决定 ;P (st | s1,s2,s3,...) =P(st | s t-1,s2,s3,...)。
- 第 i 时刻的接收信号 oi 只由发送信号 si 决定(又称为独立输出假设, 即 P(o1,o2,o3,...|s1,s2,s3....) = P(o1|s1) * P(o2|s2)*P(o3|s3)...。
基于马尔可夫假设和独立输出假设,有
![]()
其中P(s t|s t-1)是转移概率,P(o t|s t)是生成概率。所以训练马尔可夫模型,就是从海量的语料数据中找到统计求出这两个概率值。
第6章 信息的度量和作用
对于一件人已经知道很多信息的事情,人对它的不确定性就很少。反之,则越多。信息的目的:是用来消除不确定性的。不确定越大,信息也就需要的越多。信息量等于不确定性的多少。
有32支球队,获得冠军如果用二进制来存储所有的可能,需要5位bit。(信息量的比特和所有可能情况的对数函数log有关)。如果每一种情况下,事情发生的概率不一样,那么信息量的度量--信息熵(单位bit)。
信息熵是对一具体变量而言的,表示某一变量的不确定性。假设有7000个汉字,每个字等概率,那么每个汉字的熵大概13bit,如果考虑常用汉字和不常用的比例时,那么大概是9bit。如果再考虑上下文的相关性,那么将减小到5bit。一本50万字的书,大约需要250万比特。因为在这过程中,人知道很多相关的信息,信息消除了不确定性,导致未知的信息量减小,熵变小。通过压缩后,而这个过程在于消除重复率,消除冗余度。一本书重复的内容越多,那么他的信息量就越小。(自然语言处理中常用到信息论思想)
信息是消除系统不确定性的唯一办法。外接引入的信息量大于不确定性后,才能去除系统的不确定性。
从上面发现,自然语言处理的关键,就在于通过统计的方式,寻找文字间的相关性,消除不确定性。
互信息:
北京下雨和旧金山下雨,两个事件似乎没关系,但是我们不能很绝对地这样认为。互信息是用来作为两个随机事件“相关性”的度量。两个随机事件X,Y他们的互信息定义为: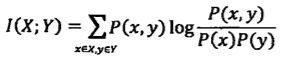
互信息被广泛运用在语言相关性的度量上。在机器翻译中,最难的问题之一就是词义的二义性。比如布什和灌木丛(Bush)通过规则分析都是名词,很难解决。最有效地办法是使用互信息。
相对熵
相对熵也叫交叉熵,也是用来衡量相关性的。但是和变量相关性的互信息不同,它是用来衡量两个取值是正数的函数的相似性。
第7章 贾里尼克
这一章主要是讲贾里尼克的故事,吴军先生其实并不是希望读者看完这个故事后,就这么草草地翻过,而是希望从伟人身上体会背后成功的因素。其实自己写博客时候,已经是书本看第二遍的时候了,此时自己已经没有第一遍那种意外的一系列感受,但是最后自己还是画出了两句我觉得特别赞的话。
- 因为犹太人重视教育的传统,所以尼克的父母从小就重视尼克的教育,为孩子提供最好的教育条件。----犹太强大的文明原因、教育的重要性
- 我一直认为,一个人想要自己在自己的领域中做到世界一流,那么他周围必须有非常多的一流的人物。----环境的重要性
第8章 布尔代数和搜索引擎
所有的搜索产品都能提炼成 下载、索引、排序 三步。
对于搜索过程中,假设用户给出一个关键词,需要判断这篇文章中是否包含这个词。如果包含,则true,否则false。比如查询的句子是 原子能AND运用NOT原子弹。 ![]()
对于索引过程中,如果一行一行地遍历,那么代价太大。可以借鉴图书馆书架上图书分类的方法。通过搜索卡,找到大概的位置,然后再在书架上查找。计算机的索引例子如下:
由于索引的表太大,所以索引表往往通过分布式存储的方式存储在不同的服务器上。
第9章 图论和网络爬虫
网络上的爬虫其实就可以当做是一张大图。将网页当做是图的结点,将网页之间的链接当做是线。网络爬虫中,一个重要的问题是判读一个页面是否已经下载过了,避免反复下载。在网络爬虫中,使用一种“散列表”(哈希表)来记录网页是否下载过。网络是非常大的,网页的数量是数以亿计的。所以,一个商业的网络爬虫需要成千上万的服务器通过高速网络链接,共同爬取的。
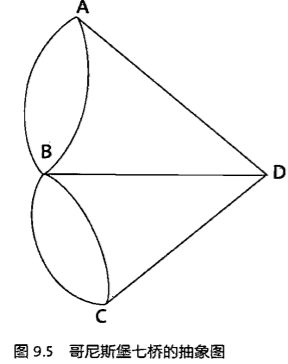
欧拉七桥
从一个节点出发,各自遍历一次所有的边和节点一次后,再次回到该节点。
网络爬虫要点
显然,各个网站最重要的是他的首页。在极端的情况下,如果爬虫很小,只能下载有限的页面,那么最应该下载的是所有网站的首页。
第10章 PageRank网页排名
网页搜素的结果的排名取决于两组信息,一组是网页质量的信息,一组是这个查询和网页相关性的信息。第10章解决的是网页质量的问题,第11章解决的是关键词和网页相关性的问题。
搜素的结果需要排序,互联网网页质量在搜素结果中排序也起到重要作用。pagerank的核心思想是:一个网页被其他页面所链接,那么它就越受到普遍的承认和认可,那么排名就越高。而每个网页间的链接也是需要考虑加权的。网页排名高的网站,它链接与该网站,那么该链接的权重就会越大。
这样,不但注意到了网页内容和查询语句的相关性,而且也注意到了网页之间的关系。计算就可以通过某种程度转换成矩阵的相乘,通过稀疏矩阵的计算方法,可以大大降低计算难度。然而,发展到至今,任何搜索引擎,十条结果都有七八条是相关的,而决定搜索质量最有用的信息是用户的点击量。
第11章 网页和查询的相关性
今天,由于商业搜索引擎已经有了大量的用户点击数据,所以,对搜索贡献最大的是根据用户对常见搜索点击网页的结果得到的概率模型。那么怎进行具体的搜索?其实,就是将搜索的句子拆分关键词,然后对关键词进行一定的计算。
比如对原子能的应用,分成原子能、的、应用,然后使用 TF-IDF来进行计算。
1、首先一个直观的感觉是,这三个词出现较多的网页应该比出现的少的网页相关性高。但是,这还需要考虑网页的长度,对关键词出现的次数进行归一化,也就是关键词的次数除以网页总字数,也就是词频(TF term frequency)。
2、当然,很容易就知道,‘原子能’ 是很专业的一个词,后者在相关性的排名上,一定比总是出现的‘的’重要的多。所以,必须对每个关键词都赋予一个权重。其中,停止词的权重需要为0。权重赋予的方法采用的方法是“逆文本频率指数” (Inverse document frequency 缩写为IDF)。
概括地讲,假定一个关键词 w 在 Dw 个网页中出现过,那么 Dw 越大,w 的权重越小,反之亦然。在信息检索中,使用最多的权重是“逆文本频率指数” ,它的公式为log(D/Dw)其中D是全部网页数。比如,我们假定中文网页数是D=10亿,应删除词“的”在所有的网页中都出现,即Dw=10亿,那么它的IDF=log(10亿/10亿)= log (1) = 0。假如专用词“原子能”在两百万个网页中出现,即Dw=200万,则它的权重IDF=log(500) =6.2。又假定通用词“应用”,出现在五亿个网页中,它的权重IDF = log(2)则只有 0.7。也就只说,在网页中找到一个“原子能”的比配相当于找到九个“应用”的匹配。
利用 IDF,上述相关性计算个公式就由词频的简单求和变成了加权求和,即 TF1*IDF1 + TF2*IDF2 +... + TFN*IDFN。在上面的例子中,该网页和“原子能的应用”的相关性为 0.0161,其中“原子能”贡献了 0.0126,而“应用”只贡献了0.0035。这个比例和我们的直觉比较一致了。
TF-IDF是一个很重要的发明。当然,对于一个写搜索引擎有兴趣的人,使用TF-IDF就足够了。
第12章 有限状态机和动态规划 在地图和本地搜索中的作用
人类书写的地址,看上去简单,但是其实这是一个复杂的上下文有关文法。是使用有限状态机进行地址识别的。
上述基于有限状态机的地址识别方法在实用中会有一些问题:当用户输入的地址不太标准或者有错别字时,有限状态机会束手无策,因为它只能进行严格匹配。(其实,有限状态机在计算机科学中早期的成功应用是在程序语言编译器的设计中。一个能运行的程序在语法上必须是没有错的,所以不需要模糊匹配。而自然语言则很随意,无法用简单的语法描述。)
为了解决这个问题,我们希望有一个能进行模糊匹配、并给出一个字串为正确地址的可能性。为了实现这一目的,科学家们提出了基于概率的有限状态机。这种基于概率的有限状态机和离散的马尔可夫链基本上等效。
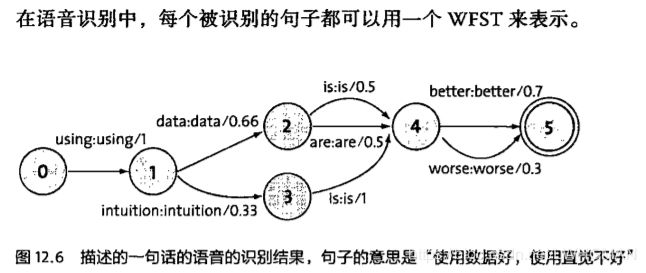
语音识别解码器基本上是基于有限状态机的原理进行开发的。不过,这些领域使用的是一种特殊的有限状态机---加权的有限状态传感器(WFST)。
好了,上述方法识别了一个地址后,接下来就是要做的是路径导航,规划出最佳的行车路线。其实所有的导航系统都是使用“动态规划”这种方法。
第13章 AK47启示
辛格做事的哲学:先帮助用户解决80%的问题,再慢慢解决20%的问题。是他能在工业界成功的一个秘诀。
第14章 余弦定理和新闻分类
新闻的分类很大程度上依靠余弦定理。
计算机其实读不懂新闻,它只能快速计算。这就要求我们设计一个算法来算出任意两篇新闻的相似性。为了做到这一点,我们需要想办法用一组数字来描述一篇新闻。
对于一篇新闻中的所有实词,我们可以计算出它们的单文本词汇频率/逆文本频率值(TF/IDF)。不难想象,和新闻主题有关的那些实词频率高,TF/IDF 值很大。我们按照这些实词在词汇表的位置对它们的 TF/IDF 值排序。比如,词汇表有六万四千个词,分别为
在一篇新闻中,这 64,000 个词的 TF/IDF 值分别为
如果单词表中的某个次在新闻中没有出现,对应的值为零,那么这 64,000 个数,组成一个64,000维的向量。我们就用这个向量来代表这篇新闻,并成为新闻的特征向量。如果两篇新闻的特征向量相近,则对应的新闻内容相似,它们应当归在一类,反之亦然。
如果两篇新闻属于同一类,它们的特征向量在某几个维度的值都比较大,而在其他维度的值都比较小。但是不同的新闻,因为文本长度的不同,他们的特征向量,各个维度的值都也不同。因此单纯比较各个维度的大小并没有太大的意义,但是向量的方向却有很大的意义。如果两个向量方向一致,说明相应的新闻用词也基本一致,因此可以通过计算两个向量的夹角,来判断对应的新闻主题是否相近,以及相近程度。如果计算两个向量的夹角,那么就得要用到余弦定理。
当两个向量正交时,夹角的余弦是0,分两篇新闻,根本没有相同的主题,他们毫不相关。
计算向量余弦的技巧
1、去掉重复计算的部分,比分母部分,也就是向量的长度,不需要重复计算
2、删除虚词,删除虚词不仅可以提高计算速度,对新闻的分类准确性也有大大的好处,因为虚词的权重其实是一种噪音,干扰分类的正常进行。
3、位置的加权,对标题和重要位置(一段话的开头和结尾,一篇文章的第1段和最后一段)的词进行额外的加权,以提高文本分类的准确性。
第16章 信息指纹及其运用
如果对文字信息进行无损压缩编码,理论上编码后的最短长度就是他的信息熵。网站是通过网址进行存储的,由于网址的长度不固定,以字符串形式查找效率很低。
将5000亿个网址随机的映射到128位二进制,也就是128比特,也就需要16个字节的存储空间。这比需要一个很长很长网址的链接要的空间小的多。 每个网址只需要占用16个字节,而不是原来的100个,这16个字节的随机数就称为该网址的信息指纹。
可以证明,只要产生随机数的算法足够好,可以保证几乎不可能有两个字符串的指纹相同,就如同不可能有两个人的指纹相同一样。由于指纹是固定的 128 位整数,因此查找的计算量比字符串比较小得多。网络爬虫在下载网页时,它将访问过的网页的网址都变成一个个信息指纹,存到哈希表中,每当遇到一个新网址时,计算机就计算出它的指纹,然后比较该指纹是否已经在哈希表中,来决定是否下载这个网页。这种整数的查找比原来字符串查找,可以快几倍到几十倍。
信息指纹的一个特征是其不可逆性, 也就是说,无法根据信息指纹推出原有信息。比如说,一个网站可以根据用户的Cookie 识别不同用户,这个 cookie 就是信息指纹。但是网站无法根据信息指纹了解用户的身份,这样就可以保护用户的隐私。
集合相同的判定
比如判定一个人是否用两个不同的邮件向共同的一组人发送垃圾邮件,而问题转化为对.邮件集合的相同性判断。
最简单的方法是对这个集合中的元素一 一进行比较。这种方法的时间复杂度是O(n^2),其中n是集合的大小.但是这种方法在面试官面前是不合格的。稍微好一点的方法是将两个集合的元素分别排序,然后按顺序比较,这样的计算时间复杂度是
O(N logN).
判定集合基本相同
可以将两组邮件按照同样的规则随机挑选几个电子邮件的地址,比如尾数是24的。如果他们的指纹相同,那么很可能接收这两个账号群发邮件的电子邮件地址清单基本相同。挑选的数量有限,通常是个位数,因此也很容易的判断是否是80%,或者90%是重复的。
上述判断,两个人两个集合,基本相同的算法有很多实际的应用。比如网页搜索中判定两个网页是否重复,只需要计算他们的网页中IDF,最大的几个词,并计算他们的信息指纹即可。判定一篇文章是否抄袭了另外一篇,具体的做法是将每一篇文章切成小片的片段,用上述的方法挑选这些片段的特征词集合并计算它的指纹,只要比较这些指纹就能找出大段相同的文字,最后根据时间先后找出原创的和抄袭的。
Youtube.的防盗版
处理时间图像首先是要找到关键帧,接下来就是要用一组信息指纹来表示这些关键帧了。有了这些信息指纹后,检测是否盗版就类似于比较两个集合元素是否相同的。
第17章 密码学
一个好的加密函数不应该通过几个自变量和函数值就能推算出函数的本身。.
密码的最高境界是,敌方在截获密码后,对我方所知的任何信息没有任何增加。用信息问的专业术语讲,就是信息量没有增加。一般来说当密码之间分布均匀,并且统计独立时提供的信息量最少。
一种加密方法,只要保证50年内计算机强行破解不了,就可以很满意了。公开密钥的任何一种具体算法,彻底破解是非常难的。
密码学的最高境界是:无论对方获取多少密文,也无法消除自己的信息情报系统的不确定性。为了达到这个目的,就不仅要做到密文之间相互无关,同时密文也要看得像完全随机的序列。
第18章:闪光的不一定是金子 谈谈搜索引擎作弊问题
自从有了搜索引擎,就有了针对搜索引擎网页排名的作弊(SPAM)。以至于用户发现在搜索引擎中排名靠前的网页不一定就是高质量的,用句俗话说,闪光的不一定是金子。
早期最常见的作弊方法是重复关键词。比如一个卖数码相机的网站,重复地罗列各种数码相机的品牌,如尼康、佳能和柯达等等。为了不让读者看到众多讨厌的关键词,聪明一点的作弊者常用很小的字体和与背景相同的颜色来掩盖这些关键词。其实,这种做法很容易被搜索引擎发现并纠正。在有了网页排名(page rank)以后,作弊者发现一个网页被引用的连接越多,排名就可能越靠前,于是就有了专门卖链接和买链接的生意。比如,有人自己创建成百上千个网站,这些网站上没有实质的内容,只有到他们的客户网站的连接。
抓作弊的方法很像信号处理中的去噪音的办法。从广义上讲,只要噪音不完全随机,并且前后有相关性,就可以检测到并消除。因为作弊者的方法不可能是随机的(否则就无法提高排名了)。而且,作弊者也不可能是一天换一种方法,即作弊方法是时间相关的。因此,搞搜索引擎排名算法的人,可以在搜集一段时间的作弊信息后,将作弊者抓出来,还原原有的排名。
第20章:不要把所有的鸡蛋放在一个篮子里 — 谈谈最大熵模型
最大熵:说白了就是要保留全部的不确定性,将风险降到最小。对一个随机事件的概率分布进行预测时,我们的预测应当满足全部已知的条件,而对未知的情况不做任何主观假设。
假如输入的拼音是"wang-xiao-bo",利用语言模型,根据有限的上下文(比如前两个词),我们能给出两个最常见的名字“王小波”和“王晓波”。至于要唯一确定是哪个名字就难了,即使利用较长的上下文也做不到。当然,我们知道如果通篇文章是介绍文学的,作家王小波的可能性就较大;而在讨论两岸关系时,台湾学者王晓波的可能性会较大。在上面的例子中,我们只需要综合两类不同的信息,即主题信息和上下文信息。
最大熵模型可以将各种信息统一整合到一个统一的模型中。他有很多良好的特性,从形式上看,它非常简单非常优美;从效果上看,它是唯一一种最能满足各种信息源的限制条件,又能保证平滑性的模型。
第21章:拼音输入法的数学原型
对汉字的编码分为两部分:分别是对拼音的编码和消除歧义性的编码。
山盟第一定律指出:对于一个信息任何编码的程度都不小于它的信息熵。
所有的输入法都是基于词输入的。如果能够更多的可以用上下文相性,就可以做到当句子中一个汉字的拼音敲完了一部分之后,这个汉字就能被提示出来。
拼音输入法就是要根据上下文再给定拼音的条件下找到一个最优的句子。
个性化语言模型
客户端有客户端优势,比如可以建立个性化的语言模型。首先,需要建立一个用户字典,然后找到大量符合用户经常输入的内容和用词习惯的语料,训练一个用户特定的语言模型,
这需要综合考虑很多因素,先前介绍的最大熵模型,把各种特征综合起来作为一个最好的采用的模型。但是训练复杂度较高,所以可采用一个简化的模型:线性插值的模型。