数据结构与算法 -- 字符串匹配 KMP算法
数据结构与算法 -- 字符串匹配 KMP算法
- 字符串匹配
- KMP算法 原理
- next 数组的推导
- KMP 算法代码实现
- KMP 算法优化
- KMP 算法优化实现
字符串匹配
题目:
给一个仅包含小写字母的字符串主串
S = abcacabdc,模式串T = abd,请查找出模式串在主中第一次出现的位置;
提示:主串和模式串均为小写字母
KMP算法 原理
对于这道算法题的解法,之前结束了BF算法和RK算法,BF算法是最好理解的,依次对比模式串和主串的各个字符,直到完全匹配,而RK算法解题,是将主串依次拆分为n个模式串长度的子串,并对其通过哈希算法换算成哈希值,进行比较。
而在利用BF算法解题时,会出现下面的情况:
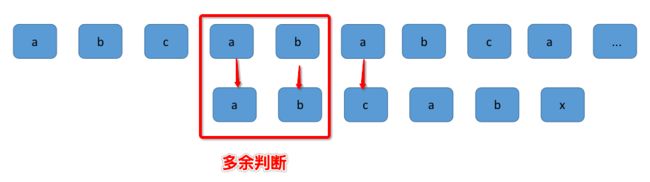
假设主串S = abcababca,模式串T = abcabx,则会出现下面的比较
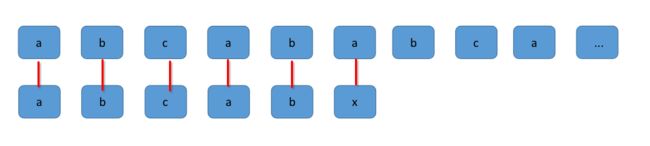
当比较到最后一个字符X时,不相等,则平移。
当进行到下面的比较时
发现前面两个对a 和b的比较是多余。
因此,可以定义一个数组next,数组的长度为模式串的长度,数组中来存储在进行匹配时,模式串标记j回溯的位置。如下图,直接从j = 3的位置开始比较。
而这就是KMP算法的原理。KMP算法主要是对模式串进行分析处理,依次找出模式串中相同的字符,当有相同字符的时候,j的回溯位置。而next数组的推导是KMP算法的关键。
next 数组的推导
-
第一种情况,模式串的字符都不相同时
假如:模式串
T = abcdex,当 j = 1 时,next[1] = 0(第一个字符匹配失败,回溯到开始的位置) 当 j = 2 时,匹配字符'b',此时 1 到 j - 1 的范围内只有'a',没有相同的字符,匹配失败时,需要从头 开始即重新匹配'a',next[2] = 1 当 j = 3 时,匹配字符'c',此时 1 到 j - 1 的范围内只有'ab',没有相同的字符,匹配失败时,需要从头 开始即重新匹配'a',next[3] = 1 依次类推... next[4] = 1 next[5] = 1 next[6] = 1
-
第二种情况,模式串有相等的字符时
假如:模式串
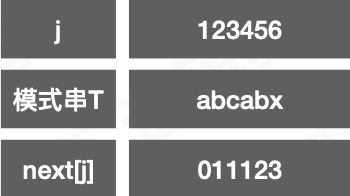
T = abcabx当 j = 1 时,next[1] = 0(第一个字符匹配失败,回溯到开始的位置) 当 j = 2 时,此时 1 到 j - 1 的范围内只有'a',没有相同的字符,匹配失败时,需要从头 开始即重新匹配'a',next[2] = 1 当 j = 3 时,此时 1 到 j - 1 的范围内只有'ab',没有相同的字符,匹配失败时,需要从头 开始即重新匹配'a',next[3] = 1 当 j = 4 时,此时 1 到 j - 1 的范围内只有'abc',没有相同的字符,匹配失败时,需要从头 开始即重新匹配'a',next[4] = 1 当 j = 5 时,此时 1 到 j - 1 的范围内只有'abca',显然前缀字符'a'与后缀字符'a'相等,匹配 失败时,可以从字符'b'开始,(P1 - Pk-1 = Pj-k+1 ... Pj-1,得到P1 = P4), 因此推出 k = 2,因此 next[5] = 2 当 j = 6 时,此时 1 到 j - 1 的范围内只有'abcab',显然前缀字符'ab'与后缀字符'ab'相等,匹配 失败时,可以从字符'c'开始,(P1 - Pk-1 = Pj-k+1 ... Pj-1,得到[P1,P2] = [P4, P5]), 因此推出 k = 3,因此 next[5] = 3
经验: 如果前后缀一个字符相等,K = 2,两个字符相等,K = 3,n个字符相等,K = n + 1
-
next 数组 回溯理解
假设主串
S = abcababca,模式串T = abcabx,i为T的开始下标,从i = 0开始,j为T结束的下标,从j = 1开始。-
i = 0, j = 1
1.默认 next[1] = 0 2.i = 0,j = 1,j < T.length,j 从 1-length 开始遍历字符串, 3.当 i=0 时,表示模式串 T 中【i,j】范围内没有找到相同的字符,所以 i 要回溯到 1 的位置, 表示 next[j] = i,即next[1] = 0; 4.或者 T[i] = T[j],表示找到相等的字符的位置,next[j] = i 5.不满足以上两个条件,将 i 回溯到 next[i] 的位置。 判断T[i] != T[j],但是 i = 0,表示【0,1】,这个范围【a】,只能从 1 的位置开始, 扩大查找相同字符的范围 所以 i++,j++,i = 1, j = 2,更新 next[j] = i,即:next[2] = 1 -
i = 1, j = 2
比较【1,2】范围内是否有相同的字符, 判断T[1] != T[2](a != b),所以 i 要回溯,i = next[i] = next[1] = 0 此时,i = 0, j = 2 -
i = 0, j = 2
比较【0,2】范围内是否有相同的字符, i = 0,又要重头开始比较,扩大查找相同字符的范围,i++,j++, i = 1,j = 3 更新 next[j] = i,即:next[3] = 1 -
i = 1, j = 3
比较【1,3】范围内是否有相同的字符, 判断T[1] != T[3](a != c),所以 i 要回溯,i = next[i] = next[1] = 0 此时,i = 0, j = 3 -
i = 0, j = 3
比较【0,3】范围内是否有相同的字符,没有相同的字符 i = 0,又要重头开始比较,扩大查找相同字符的范围,i++,j++, i = 1,j = 4 更新 next[j] = i,即:next[4] = 1 -
i = 1,j = 4
比较【1,4】范围内是否有相同的字符, 判断T[1] = T[4](a = a),扩大查找范围,是否有更长的相同字符 i++,j++, i = 2, j = 5 更新 next[j] = i,即:next[5] = 2 -
i = 2, j = 5
比较【2,5】范围内是否有相同的字符, 判断T[2] = T[5](b = b),扩大查找范围,是否有更长的相同字符 i++,j++, i = 3, j = 6 更新 next[j] = i,即:next[6] = 3 j = 6时,模式串 T 已经处理查找完毕
-
总结:
在求解 next 数组的4中情况
1. 默认 next[1] = 0
2. 当 i= 0,表示当前的比较应该从头开始,则i++,j++,next[j] = i
3. 当 T[i] = T[j],表示两个字符相等,则i++,j++,next[j] = i
4. 当 T[i] != T[j],表示两个字符不相等,则将 i 回退到合理的位置,则 i = next[i]
- next 数组求解 代码
// T 为模式串,T[0]位置存储T的长度
void get_next(String T,int *next){
int i,j;
j = 1;
i = 0;
next[1] = 0;
//abcdex
//遍历T模式串, 此时T[0]为模式串T的长度;
//printf("length = %d\n",T[0]);
while (j < T[0]) {
//printf("i = %d j = %d\n",i,j);
if(i ==0 || T[i] == T[j]){
//T[i] 表示后缀的单个字符;
//T[j] 表示前缀的单个字符;
++i;
++j;
next[j] = i;
//printf("next[%d]=%d\n",j,next[j]);
}else
{
//如果字符不相同,则i值回溯;
i = next[i];
}
}
}
KMP 算法代码实现
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 100 /* 存储空间初始分配量 */
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */
typedef int ElemType; /* ElemType类型根据实际情况而定,这里假设为int */
typedef char String[MAXSIZE+1]; /* 0号单元存放串的长度 */
//----字符串相关操作---
/* 生成一个其值等于chars的串T */
Status StrAssign(String T,char *chars)
{
int i;
if(strlen(chars)>MAXSIZE)
return ERROR;
else
{
T[0]=strlen(chars);
for(i=1;i<=T[0];i++)
T[i]=*(chars+i-1);
return OK;
}
}
Status ClearString(String S)
{
S[0]=0;/* 令串长为零 */
return OK;
}
/* 输出字符串T。 */
void StrPrint(String T)
{
int i;
for(i=1;i<=T[0];i++)
printf("%c",T[i]);
printf("\n");
}
/* 返回串的元素个数 */
int StrLength(String S)
{
return S[0];
}
//----KMP 模式匹配算法---
//1.通过计算返回子串T的next数组;
//注意字符串T[0]中是存储的字符串长度; 真正的字符内容从T[1]开始;
void get_next(String T,int *next){
int i,j;
j = 1;
i = 0;
next[1] = 0;
//abcdex
//遍历T模式串, 此时T[0]为模式串T的长度;
//printf("length = %d\n",T[0]);
while (j < T[0]) {
//printf("i = %d j = %d\n",i,j);
if(i ==0 || T[i] == T[j]){
//T[i] 表示后缀的单个字符;
//T[j] 表示前缀的单个字符;
++i;
++j;
next[j] = i;
//printf("next[%d]=%d\n",j,next[j]);
}else
{
//如果字符不相同,则i值回溯;
i = next[i];
}
}
}
//输出Next数组值
void NextPrint(int next[],int length)
{
int i;
for(i=1;i<=length;i++)
printf("%d",next[i]);
printf("\n");
}
int count = 0;
//KMP 匹配算法(1)
//返回子串T在主串S中第pos个字符之后的位置, 如不存在则返回0;
int Index_KMP(String S,String T,int pos){
//i 是主串当前位置的下标准,j是模式串当前位置的下标准
int i = pos;
int j = 1;
//定义一个空的next数组;
int next[MAXSIZE];
//对T串进行分析,得到next数组;
get_next(T, next);
count = 0;
//注意: T[0] 和 S[0] 存储的是字符串T与字符串S的长度;
//若i小于S长度并且j小于T的长度是循环继续;
while (i <= S[0] && j <= T[0]) {
//如果两字母相等则继续,并且j++,i++
if(j == 0 || S[i] == T[j]){
i++;
j++;
}else{
//如果不匹配时,j回退到合适的位置,i值不变;
j = next[j];
}
}
if (j > T[0]) {
return i-T[0];
}else{
return -1;
}
}
//KMP算法调用
StrAssign(s1,"abcababca");
printf("主串为: ");
StrPrint(s1);
StrAssign(s2,"abcdex");
printf("子串为: ");
StrPrint(s2);
Status = Index_KMP(s1,s2,1);
printf("主串和子串在第%d个字符处首次匹配(KMP算法)[返回位置为负数表示没有匹配] \n",Status);
KMP 算法优化
假设主串S = aaaabcde,模式串T = aaaaax,在对 next数组求解,得到:
next = [0, 1, 2, 3, 4, 5],在匹配的过程中,会出现下面情况:
依次字符匹配,当匹配到主串 i=5, 模式串 j=5 时, b != a
则,将 j 回溯到 j = next[j] = 4 的位置
此时依然是 b != a,继续回溯,直到 j = 0
这样前面的几次回溯匹配是没有必要的
所以,我们可以对其进行优化,可以复用前面重复字符的next值,在回溯是时候直接回溯到正确的位置。减少不必要的匹配过程。例如下面的示例:
假设 模式串T = ababaaaba,在求解 nextVal 数组时:
当 j = 1,nextVal[1] = 0
当 j = 2,第二个字符'b',第一个字符'a',不相等,nextVal[2] = next[2] = 1
当 j = 3,第三个字符'a',第一个字符'a',相等,nextVal[3] = nextVal[1] = 0
当 j = 4,第四个字符'b',其 next = 2,与第二个字符'b',相等,nextVal[4] = nextVal[2] = 1
当 j = 5,第五个字符'a',其 next = 3,与第三个字符'a',相等,nextVal[5] = nextVal[3] = 0
当 j = 6,第六个字符'a',其 next = 4,与第四个字符'b',不相等,nextVal[6] = next[6] = 4
当 j = 7,其 next = 2,与第二个字符'b',不相等,nextVal[7] = next[2] = 2
当 j = 8,其 next = 2,与第二个字符'b',相等,nextVal[8] = nextVal[2] = 1
当 j = 9,其 next = 3,与第二个字符'a',相等,nextVal[9] = nextVal[3] = 0
在求解 nextVal 数组时:
1. 默认nextVal【0】= 0
2. T【i】= T【j】,且++i, ++j 后,T【i】依旧等于 T【j】,则 nextVal【i】 = nextVal【j】
3. i=0,表示从头开始,i++,j++ 后,T【i】!= T【j】,则 nextVal = j
4. T【i】= T【j】,且++i, ++j 后,T【i】!= T【j,则 nextVal = j
5. T【i】!= T【j】,则将 i 退回到合理的位置, i = nextVal【i】
KMP 算法优化实现
void get_nextVal(String T,int *nextVal){
int i,j;
j = 1;
i = 0;
nextVal[1] = 0;
while (j < T[0]) {
if (i == 0 || T[i] == T[j]) {
++j;
++i;
//如果当前字符与前缀不同,则当前的j为nextVal 在i的位置的值
if(T[i] != T[j])
nextVal[j] = i;
else
//如果当前字符与前缀相同,则将前缀的nextVal 值赋值给nextVal 在i的位置
nextVal[j] = nextVal[i];
}else{
i = nextVal[i];
}
}
}