后缀排序SA 详解+模板
这里以洛谷P3809为例题。
题目描述
读入一个长度为 nn 的由大小写英文字母或数字组成的字符串,请把这个字符串的所有非空后缀按字典序从小到大排序,然后按顺序输出后缀的第一个字符在原串中的位置。位置编号为 11 到 nn 。
输入输出格式
输入格式:一行一个长度为 nn 的仅包含大小写英文字母或数字的字符串。
一行,共n个整数,表示答案。
题解:
这里介绍的是倍增法(O(nlogn)),有兴趣的同学们可以去了解一下DC3法(O(n))。
后缀数组(SA)是啥?
所谓字符串的一个后缀就是从此字符串任意i位置一直到最末的字符为止所构成的一个新字符串。而题目要求的后缀数组即是让我们求出这个字符串的所有非空后缀按字典序从小到大排序,然后按顺序输出后缀的第一个字符在原串中的位置。
如何求解?
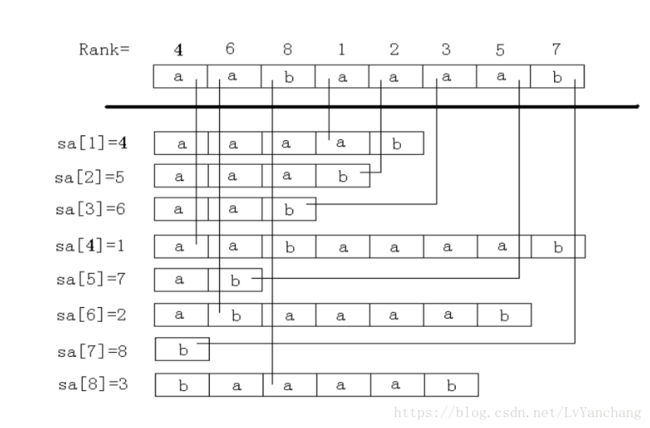
我们一般用常数小,方便写的倍增法解决。我们首先单独处理解决每个字符的排序rank值,然后把这一次的SA作为初始值,开始倍增操作。我们已经知道了i往后2^k这么长的字符串的排名,如何推得i往后2^(k+1)长度字符串的排名呢?也就是说这个字符串分为两段,我们知道前一段的排名和后一段的排名,以前一段的排名作为第一关键字,后一段的排名作为第二关键字,一遍排序后即可求出这一整段的排名了。
如图(原出处:https://blog.csdn.net/yxuanwkeith/article/details/50636898):
代码:
我在做这道题的时候其实遇到了一点小小的波折,第一次的代码总是TLE,死活卡不过去:
70分代码:
#include
#include
#include
using namespace std;
const int Maxn=1000005;
char a[Maxn];
int n,f[Maxn][25],rank[Maxn],tp1[Maxn],tp2[Maxn];
int sa[Maxn],t[Maxn],num1[Maxn];
int num2[Maxn],sum[Maxn],now[Maxn];
int main(){
scanf("%s",a+1);
n=strlen(a+1);
for(int i=1;i<=n;i++){
t[a[i]-'0'+1]++;
}
for(int i=1;i<=200;i++){
t[i]+=t[i-1];
sum[i]=t[i-1]+1;
}
for(int i=n;i>=1;i--){
rank[i]=sum[a[i]-'0'+1];
sa[t[a[i]-'0'+1]--]=i;
}
for(int j=1;(1<=1;i--){tp2[sa[i]]=rank[sa[i]]=sum[num2[sa[i]]];now[t[num2[sa[i]]]--]=sa[i];}
for(int i=1;i<=n;i++){sa[i]=now[i];}
memset(t,0,sizeof(t));
for(int i=1;i<=n;i++)t[num1[i]]++;
for(int i=1;i<=n;i++){t[i]+=t[i-1];sum[i]=t[i-1]+1;}
for(int i=n;i>=1;i--){rank[sa[i]]=sum[num1[sa[i]]];now[t[num1[sa[i]]]--]=sa[i];}
for(int i=1;i<=n;i++){sa[i]=now[i];}
for(int i=1;i<=n;i++){
if(tp1[sa[i]]==tp1[sa[i-1]]){
if(tp2[sa[i]]==tp2[sa[i-1]])rank[sa[i]]=rank[sa[i-1]];
else rank[sa[i]]=i;
}
else{
rank[sa[i]]=i;
}
}
}
for(int i=1;i<=n;i++){
printf("%d ",sa[i]);
}
return 0;
}
rank[sa[i]]=i的次数,也就是如果每个位置的排名都已经没有重复的了,那么我们再往后搜也无法改变SA的结果了。
没想到居然,整整快了将近10s??
AC代码:
#include
#include
#include
using namespace std;
const int Maxn=2000005;
char a[Maxn];
int n,f[Maxn][25],rank[Maxn],tp1[Maxn],tp2[Maxn];
int sa[Maxn],t[Maxn],num1[Maxn];
int num2[Maxn],sum[Maxn],now[Maxn],cnt;
int main(){
scanf("%s",a+1);
n=strlen(a+1);
for(int i=1;i<=n;i++){
t[a[i]-'0'+1]++;
}
for(int i=1;i<=200;i++){
t[i]+=t[i-1];
sum[i]=t[i-1]+1;
}
for(int i=n;i>=1;i--){
rank[i]=sum[a[i]-'0'+1];
sa[t[a[i]-'0'+1]--]=i;
}
for(int j=1;(1<=1;--i){tp2[sa[i]]=rank[sa[i]]=sum[num2[sa[i]]];now[t[num2[sa[i]]]--]=sa[i];}
for(int i=1;i<=n;++i){sa[i]=now[i];t[i]=0;}
for(int i=1;i<=n;++i)t[num1[i]]++;
for(int i=1;i<=n;++i){t[i]+=t[i-1];sum[i]=t[i-1]+1;}
for(int i=n;i>=1;--i){rank[sa[i]]=sum[num1[sa[i]]];now[t[num1[sa[i]]]--]=sa[i];}
for(int i=1;i<=n;++i){sa[i]=now[i];}
cnt=0;
for(int i=1;i<=n;++i){
if(tp1[sa[i]]==tp1[sa[i-1]]){
if(tp2[sa[i]]==tp2[sa[i-1]])rank[sa[i]]=rank[sa[i-1]];
else rank[sa[i]]=i,cnt++;
}
else{
rank[sa[i]]=i,cnt++;
}
}
if(cnt>=n)break;
}
for(int i=1;i<=n;i++){
printf("%d ",sa[i]);
}
return 0;
}