机器学习理论篇之CNN 卷积神经网络

CNN 卷积神经网络

一.定义

卷积神经网络（ConvolutionalNeural Network,CNN）是一种前馈神经网络，对于大型图像处理有出色表现。[1] 它包括卷积层(convolutionallayer)和池化层(poolinglayer)。由于该网络避免了对图像的复杂前期预处理，可以直接输入原始图像，因而得到了更为广泛的应用。

CNN的基本结构包括两层，其一为特征提取层，每个神经元的输入与前一层的局部接受域相连，并提取该局部的特征。一旦该局部特征被提取后，它与其它特征间的位置关系也随之确定下来；其二是特征映射层，网络的每个计算层由多个特征映射组成，每个特征映射是一个平面，平面上所有神经元的权值相等。特征映射结构采用影响函数核小的sigmoid函数作为卷积网络的激活函数，使得特征映射具有位移不变性。

二.与全连接网络区别：
全连接神经网络：
结构：每两层间所有节点都有连接
输入输出：输入特征，输出预测
参数个数：求和（前层神经元个数×后层神经元个数+后层（偏置））
缺点：参数个数如果过多，会导致计算慢且易发生过拟合。

卷积神经网络：
结构：每两层间节点部分连接，为了展示每一层神经节点的维度，一般会将每一层卷积层的节点组织成一个三维矩阵。前几层中每一个节点只和上一层中部分的节点相连。
输入输出：输入特征，输出预测
参数个数：卷积核体积+卷积核个数（长×宽×高+个数）
目的：借助卷积核提取特征点的过程。
作用：高层次抽象特征，精简特征点。

全连接到卷积网络：二维到三维的过程，灰度值到RGB的操作。

三.卷积神经网络的五大组成部分：
1.输入层：输入图片的像素矩阵，三维，有深度，代表RGB
2.卷积层：每一个节点的输入是上一层神经网络的一小块，这个小块大小有3×3或者5×5.卷积层试图将神经网络中的每一小块进行更加深入地分析，从而抽象程度更高的特征。
3.池化层：池化层不改变三维矩阵的深度，但是它可以缩小矩阵的大小。池化操作可以认为是将一张分辨率较高的图片转化为分辨率较低的图片。
4.全连接层：经过几轮卷积层和池化层处理之后，在卷积神经网络的最后一般会是1到2个全连接层来给出最后的分类结果。
5.Softmax层：用于分类问题，给出不同分类的概率情况。

四.两个核心结构：
1.卷积核（过滤器）：
卷积操作：有深度概念，深度为3的卷积核，就是一个3×3×3的立方体。每次优化的是一个小方格。
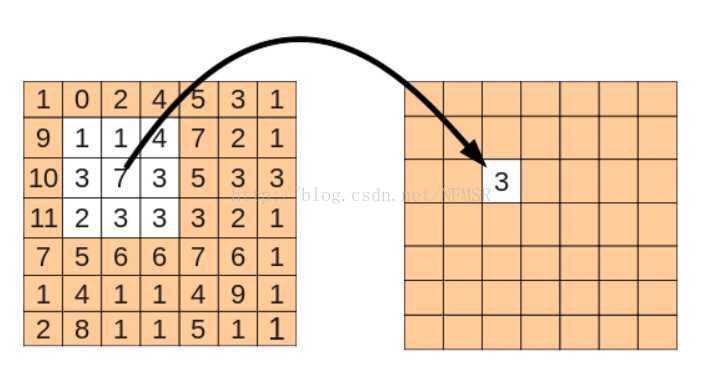
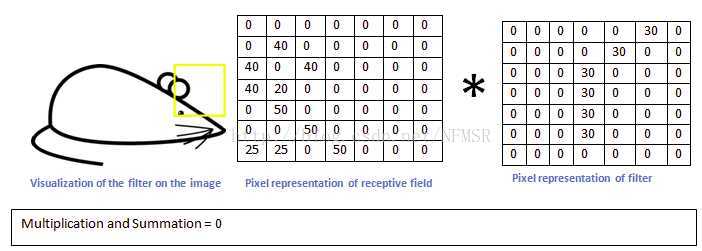
卷积层前向传播：就是拿卷积核中的参数，和像素点进行乘积，然后求和。左上，左下，右上，右下的顺序。

卷积核的深度由样本决定。

我们可以改变卷积核的个数，大小（长和宽），步长，还要padding（要不要填0）。。

大小：卷积核的长×宽，常用的有3×3, 5×5.
Padding:当过滤器大小不为1×1是，卷积层前向传播得到的矩阵尺寸要小于当前层矩阵的尺寸。

为了避免尺寸的变化，我们可以在当前矩阵的边界上加入全0填充（zero-padding），这样可以使得卷积层的前向传播结果矩阵大小和当前矩阵保持一致。

步长：分为在长度和高度上的移动长度，即每一次卷积核移动的长度，这也会改变结果矩阵的大小。

结果矩阵大小公式：

全0填充下：
结果矩阵长度=（输入长度/长度方向步长）向上取整
结果矩阵宽度=（输入宽度/宽度方向步长）向上取整


不使用全0填充下：
结果矩阵长度=（（输入长度-卷积核长度+1）/步长）向上取整
结果矩阵宽度=（（输入宽度-卷积核宽度+1）/步长）向上取整

性质：(共享权值)每一个卷积层中使用的过滤器（卷积核）中的参数都是一样的。因为共享过滤器的参数可以使得图像上的内容不受位置影响。而且共享每一个卷积层中过滤器的参数可以巨幅减少神经网络中的参数。

2.池化层：
在卷积层之间往往加上一个池化层，池化层可以非常有效地缩小矩阵的尺寸，从而减小最后全连接层中的参数，使用池化层既可以加快计算速度也有防过拟合问题的作用。
池化层前向传播也是移动类似与过滤器的结构来完成的。不过池化层中过滤器结果不是计算加权和。而是采取更加简单的求最大值或平均值的方法，因此这里就分为 最大池化层和平均池化层。
还有个 区别就是卷积层上的过滤器是横跨整个深度的，而池化层使用的过滤器是只影响一个深度上的节点.。所以池化层的过滤器除了在长和宽两个维度上移动之外，它还需要在深度这个维度上移动。
池化层主要用于减少矩阵的长和宽。虽然池化层也可以减少矩阵的深度，但是矩阵中一般不这么做。

五.工作原理

链接：https://www.zhihu.com/question/39022858

机器之心那篇文章好好看看很有启发，不过有点长。

下面是我摘录的第一个回答，感觉也是挺不错的，如果不想点链接的话，就看看这个。

也就相当于对原矩阵，按照顺序将各区域元素与W矩阵相乘，W矩阵为

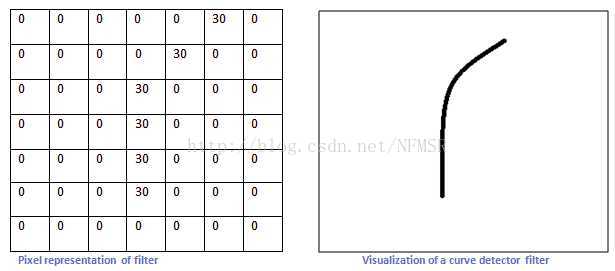
这也被称作核(Kernel,3X3)这就是核（疑问？这个核是卷积核？还是池化层的核！！这里感觉原文有问题，感觉卷积核的话应该是对应位置相乘然后求和的，不会做求平均值的操作。。）

其处理效果如下：

也就是用这个核对图像进行操作，想当与对图像进行了低通滤波，因此这个核也被称为滤波器，整个操作过程按照概念称为卷积。

扩展来讲，对二维图像的滤波操作可以进行卷积，比如常见的高斯滤波，拉普拉斯滤波（算子），等。

滤波器跟卷积神经网络有什么关系呢。不如我们预想一个识别问题：我们要识别图像中的某种特定曲线，也就是说，这个滤波器要对

这种曲线有很高的输出，对其他形状则输出很低，这也就像我们设计的滤波器和想要识别的曲线如下：

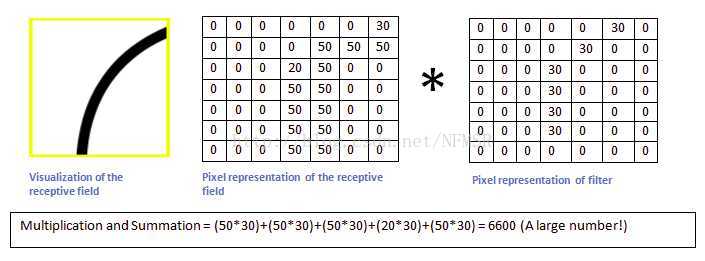
假设上面的核（滤波器）按照卷积顺序沿着下图移动：

那么当它移动到上面的位置时，按照矩阵操作，将这个区域的图像像素值与滤波器相乘，我们得到一个很大的值（6600）：

而当这个滤波器移动到其他区域时，我们得到一个相对很小的值：

如此，我们对整个原图进行一次卷积，得到的结果中，在那个特定曲线和周边区域，值就很高，在其他区域，值相对低。这就是一张

激活图，对应的高值区域就是我们所要检测曲线的位置。

卷积神经网络的第一个卷积层的滤波器用来检测低阶特征，比如边、角、曲线等。随着卷积层的增加，对应滤波器检测的特征就更加

复杂理性情况下，也是我们想要的情况）。比如第二个卷积层的输入实际上是第一层的输出（滤波器激活图），这一层的滤波器便是

用来检测低价特征的组合等情况（半圆、四边形等），如此累积，以检测越来越复杂的特征。

所以，在相当程度上，构建卷积神经网络的任务就在于构建这些滤波器。也就是，将这些滤波器变成这样(改变滤波器矩阵的值，也就是Weight)的——能识别特定

的特征。这个过程叫做训练。

在训练开始之时，卷积层的滤波器是完全随机的，它们不会对任何特征激活（不能检测任何特征）。这就像刚出生的孩子，TA不知道什么是人脸、什么是狗，什么

是上下左右。TA需要学习才知道这些概念，也就是通过接触人脸、狗、上下左右，并被告知这些东西分别是人脸、狗、上下左右。然后TA才能在头脑中记住这些概

念，并在之后的某一次见到之后能准确的给出结果。

把一个空白的滤波，修改其权重(weights)以使它能检测特定的模式，整个过程就如工程里面的反馈。

这是另一篇博客https://www.cnblogs.com/zf-blog/p/6075286.html，感觉对立体的卷积过程讲的还是比较清楚

六 .tensorflow实现需要用到的函数

1.卷积：
tf.nn.convzd(
第一个参数：节点矩阵  eg：shape[batch,28,28,1]  # batch一次喂的个数，28×28面积，1深度
第二个参数：卷积层的权重变量  eg：shape[5,5,3,16]5×5 核的面积，3核的深度（当前层的深度），16核的个数（过滤器的深度）
第三个参数：核滑动步长  eg：strides=[1,1,1,1] 第一个1和最后一个1是固定，中间的两个是步长。
第四个参数：padding=“SAME”  #使用全0填充   结果：（输入长度）/步长
            padding=“VALID” # 不使用全0填充  结果：（输入长度-核的长度+1）/步长，向上取整

tf.nn.bias_add(conv,biased)
第一个参数conv是卷积产生的结果，
第二个参数biases是偏置项
函数解释：tf.nn.bias_add提供了一个方便的函数给每一个节点加上偏置项。注意这里不能直接使用加法，因为矩阵上不同位置上的节点都需要加上同样的偏置项。卷积后产生的矩阵虽然可能有所减小，但是我们只有一个偏置项，而矩阵大小不是1×1。.

2.池化：
pool=tf.nn.max_pool(
第一参数：输入描述  eg[batch,28,28,6]
第二个参数：核描述 eg：ksize=[1 ,2,2,1]第一个和第四个固定，2×2是过滤器的尺寸
第三个参数：核滑动步长eg：strides=[1 ,2,2,1]第一个和第四个固定，2,2是长和宽方向的步长
第四个参数：padding=“SAME”/”VALID”
tf.nn.avg_pool用法相同

3.dropout：
dropout在训练时会随机将部分节点的输出改为0,dropout可以避免过拟合问题，从而使得模型在测试数据上的效果更好，dropout一般只会在全连接层而不是在卷积层或者池化层使用。
if train : 输出=tf.nn.dropout(上层输出，置零概率)

七.经典卷积网络模型：
卷积层过滤器深度逐层递增，一般每经过池化层后，卷积层过滤器深度×2，卷积层步长一般为1。
池化层过滤器边长一般为2或者3,步长也一般2或者3
正则表达式(公式)：输入层———（卷积层+——池化层？）+——全连接层+
+表示一层或多层，？表示0层或1层。
最多连续使用三层卷积层。

1.Lenet-5模型  ：（1998年提出）共7层
输入32×32×1
第一层，卷积层：cov1：5×5×1×6 （1是深度，6是核的个数）， 非0 填充，步长1        #32-5+1/1=28
输出28×28×6
第二层，池化层：pooling：2×2 , 非0填充，步长2   #28/2=14
输出：14×14×6
第三层，卷积层：cov2：5×5×6×16（前三个核体积，16核的个数），非0填充，步长为1
输出：10×10×16
第四层,池化层：pooling：2×2 , 非0填充，步长2
输出：5×5×16
第五层，全连接层：
拉直：[1,5×5×16]
输出120个节点
总共参数个数：5×5×16×120+120=48120个参数。
第六层，全连接层：
输入节点个数120个
输出节点个数84
总共参数：120×84+84=10164个
第七层，全连接层
输入节点个数84个
输出节点个数：10个
总共参数：84×10+10=850个

缺点：无法很好的处理类似ImageNet这样大的图像数据集。

2.Inception-v3模型：（2015年提出）
在LeNet-5模型中，不同卷积层通过串联方式连接在一起。
而在Inception-v3模型中的Inception结构是将不同的卷积层通过并联的方式结合在一起。
Inception模块中，同时使用所有不同尺寸（边长1,3,5）的过滤器，然后在将得到的矩阵拼接起来。
Inception会首先使用不同尺寸的过滤器处理输入矩阵，虽然过滤器的大小不同，但如果所有过滤器都使用全0填充且步长为1,那么前向传播得到的结果矩阵的长和宽都与输入矩阵一致。这样经过不同过滤器处理的结果矩阵可以拼接一个更深的矩阵。可以将它们在深度这个维度上组合起来。
Inception-v3模型总共有46层，由11个模块组成，总共有96个卷积层。
Tensorflow中一般使用TensorFlow-Slim工具来创建。

//TensorFlow-Slim可以在一行中实现一个卷积层的前向传播。
net=slim.conv2d(input,32,[3,3])
参数：（必选）
第一个参数：输入节点矩阵。
第二个参数：当前卷积层过滤器的深度，
第三个参数：过滤器的尺寸。

可选：移动步长，是否使用全0填充，激活函数的选择，变量的命名空间。