8、聊聊java中的进制问题
java中的进制也算是面试中经常会遇到的一个知识点,不管是计算问题,还是涉及到的基础知识。因此这篇文章对其进行一个整理。主要参考了慕课网上的视频,特在此说明。不管是你初学者还是工作中,又或者是找工作中。本文都能对你有所帮助。
本篇文章主要解决以下几个问题:
1、二进制的历史
2、java中的进制转换
3、java中的移位运算
4、数据大小端问题
5、进制在java中的使用
下面我们就针对这些问题,来分析一下java中的进制。
一、二进制的历史
这一小节优点闲扯淡的感觉,要说二进制的历史其实可以追述到一个大数学家莱布尼茨。当时有一个法国传教士白晋来到了咱们中国,走的时候带走了中国的一本古书《易经》,白晋回到德国之后,莱布尼茨就看了《易经》里面的伏羲八卦图。突然灵机一动(动没动是我瞎猜的),就发明了二进制。不管不管怎么样二进制的由来或多或少都收到了中国伏羲八卦图的影响。

这就是伏羲八卦图,怎么想到的我也不知道,不过你仔细观察看一下,最上面的乾卦三横实线,顺时针转动,实线变虚线。你可以想象成从000到111的变化。
二、java中的进制转换
其实常见的进制转换主要有以下几种:
(1)十进制转二进制
(2)十进制转八进制
(3)十进制转十六进制
(4)二进制转十进制
(5)八进制转十进制
(6)十六进制转十进制
十进制的范围就是0-9,二进制的范围是0-1,八进制的范围是0-7,十六进制的范围是0-f。java提供了工具类来实现进制的转换。因此在笔试的时候你可以直接使用。
public class Test{
public static void main(String[] args) {
int a=20;
//十进制转其他进制
String a_to_hex=Integer.toHexString(a);
String a_to_octal=Integer.toOctalString(a);
String a_to_binary=Integer.toBinaryString(a);
//其他进制转十进制
String hex_to_10 = Integer.valueOf("f",16).toString();
String octal_to_10 = Integer.valueOf("17",8).toString();
String binary_to_10 = Integer.valueOf("101",2).toString();
System.out.println("十进制20转二进制:"+a_to_hex);
System.out.println("十进制20转八进制:"+a_to_octal);
System.out.println("十进制20转十六进制:"+a_to_binary);
System.out.println("二进制101转十进制:"+binary_to_10);
System.out.println("八进制17转十进制:"+octal_to_10);
System.out.println("十六进制f转十进制:"+hex_to_10);
}
}
然后我们运行一下就可以直接看到结果了。比较简单。
三、java中的位操作
java中为了使得运算方便而且快速,可以直接进行位操作进行运算。常见的有以下六种:
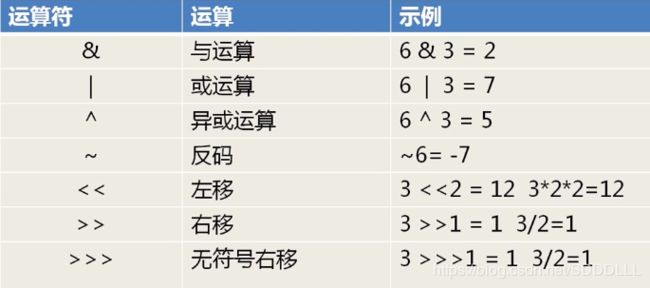






上面这几张图,主要是概念用法。下面我们看位运算的几个应用:
(1) 判断int型变量a是奇数还是偶数
a&1 = 0 偶数
a&1 = 1 奇数
(2) 取int型变量a的第k位 (k=0,1,2……sizeof(int)),即a>>k&1 (先右移再与1)
(3) 将int型变量a的第k位清0,即a=a&~(1<
(4) 将int型变量a的第k位置1,即a=a|(1<
(5) int型变量循环左移k次,即a=a<
(6) int型变量a循环右移k次,即a=a>>k|a<<16-k (设sizeof(int)=16)
(7)对于一个数 x >= 0,判断是不是2的幂。
boolean power2(int x){
return ( (x&(x-1))==0) && (x!=0);
}
(8)不用temp交换两个整数
void swap(int x , int y){
x ^= y;
y ^= x;
x ^= y;
}
(9)计算绝对值
int abs( int x ){
int y ;
y = x >> 31 ;
return (x^y)-y ;
}
(10)取模运算转化成位运算 (在不产生溢出的情况下)
a % (2^n) 等价于 a & (2^n - 1)
(11)乘法运算转化成位运算 (在不产生溢出的情况下)
a * (2^n) 等价于 a<< n
四、大小端问题
1、小端法(Little-Endian)
低位字节排放在内存的低地址端即该值的起始地址,高位字节排放在内存的高地址端
2、高端法(Big-Endian)
高位字节排放在内存的低地址端即该值的起始地址,低位字节排放在内存的高地址端
为什么会有大小端呢?
在计算机中,每个地址单元都对应着一个字节(8bit)数据。java中int类型占据4个字节,long占据8个字节,计算机是由32位和64位之分的,处理器因此也就是有32位和64位之分,现在有一个32位的处理器,突然来了一个8字节64位的数据,这时候处理器就不能一下子处理了,于是就要把8个字节的数据分开存放,这一存放就要分出个高地了,谁在前面谁在后面的问题。
比如说下面的这个例子(前几天做的一道面试原题):
32bit宽的数0x12345678在Little-endian模式CPU内存中的存放方式(假设从地址0x2000开始存放)为:
| 内存地址 | 0x2000 | 0x2001 | 0x2002 | 0x2003 |
|---|---|---|---|---|
| 存放内容 | 0x78 | 0x56 | 0x34 | 0x12 |
因此这就是0x87654321存放。
而在Big-endian模式CPU内存中的存放方式则为:
| 内存地址 | 0x2000 | 0x2001 | 0x2002 | 0x2003 |
|---|---|---|---|---|
| 存放内容 | 0x12 | 0x34 | 0x56 | 0x78 |
这个在大端模式下是正常的。牢记牢记。
五、进制的使用场景
上面在介绍的时候其实说了一部分,但是这里再简单的举个例子,最常见的例子就是序列化。我们知道客户端我们可以使用java语言编写,但是服务器就不一定了,可能是java,也可能是C++,这时候传输数据怎么办呢?这俩语言之间又相互不认识。这时候客户端java就可以把我们的数据切分序列化成二进制数,二进制数计算机到哪都能认识,这时候把二进制数发送到服务端,服务端按照一定的规则反序列化就OK了。
对于字符串来说那就是太简单了,我们直接getBytes就可以转化成byte。但是对于int该怎么办呢?我们给出一个例子,其他的可以自己测试一下。
public class Test{
public static void main(String[] args) {
byte[] result = int2byte(8421);
for(byte i :result) {
System.out.println(i);
}
}
public static byte[] int2byte(int value) {
//int是4个字节就初始化为4
byte[] array = new byte[4];
for(int i=0;i<4;i++) {
array[i]= (byte)((value >> i*8) & 0xff);
}
return array;
}
}
atic byte[] int2byte(int value) {
//int是4个字节就初始化为4
byte[] array = new byte[4];
for(int i=0;i<4;i++) {
array[i]= (byte)((value >> i*8) & 0xff);
}
return array;
}
}
``
OK,进制中常见的问题先列出这么多,欢迎批评指正。