Python学习笔记（四）——基于SVD的协同过滤（推荐算法）

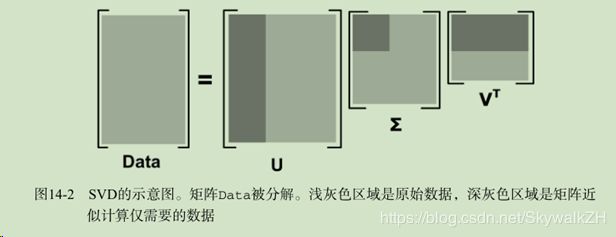
奇异值分解（Singular value decomposition）是一种矩阵分解技术，也是一种提取信息的方法。将一个比较复杂的矩阵用更小更简单的3个子矩阵的相乘来表示，这3个小矩阵描述了大矩阵重要的特性，可以起到降维简化数据，去除数据噪声的作用。

 

一、SVD定义：

1.回顾特征值和特征分解：

①特征值

如果一个向量v是 NxN 方阵A的特征向量，那么可以用下式表示：

其中λ就被称为特征向量v对应的特征值，一个矩阵的一组特征向量是n个线性无关的特征向量。

②特征分解

令A是一个 N×N 的方阵，且有 N 个线性无关的特征向量。这样，A 可以被分解为：

其中Q是 NxN 方阵，第i列为A的特征向量， Λ 是对角矩阵，其对角线上的元素为对应的特征值，也即

注意：只有可对角化矩阵才可以作特征分解

一般而言，​一般被正交化，（特征向量组​未被正交化也可组成Q）也就是说,两边同乘以,可以得到,故表达式也可以写成下式：

 

2.SVD定义：

任意一个m*n的矩阵A都可以像上式一样分解，其中得到的U是一个m*m的方阵（里面的向量是正交的，U里面的向量称为左奇异向量），Σ是一个 m* n的矩阵（除了对角线的元素都是0，对角线上的元素称为奇异值），是一个 n*n 的矩阵(里面的向量也是正交的，V里面的向量称为右奇异向量）

若先进行计算，可以得到一个 n*n的方阵，用这个方阵进行特征分解可以得到：

其中v就是我们V矩阵里的右奇异向量，此外我们还可以得到：

其中就是我们Σ矩阵里的奇异值，u就是U矩阵里的左奇异向量。

 

奇异值σ跟特征值类似，在矩阵Σ中也是从大到小排列，而且σ的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说，选前k个奇异值来近似原矩阵，如下式：

                                                            

k是一个远小于n的数，故U ， Σ， 三个面积之和远小于原矩阵，即所需存储空间小于原矩阵，想要以压缩空间存储原数据的话，就可以只存U ， Σ， 这三个小矩阵。

 

二、SVD作用：

1.主成分分析（PCA）：

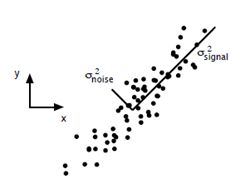
假设x-y空间存在如上图的一组数据，若要选一条直线进行对原数据进行近似拟合，我们会选择signal方向的直线（方差大）而不是noise方向的直线（方差小）。

PCA简单来说，就是对原始的空间中顺序地找一组相互正交的坐标轴，第一个轴是使得方差最大的，第二个轴是在与第一个轴正交的平面中使得方差最大的，第三个轴是在与第1、2个轴正交的平面中方差最大的.......这样假设在N维空间中，我们可以找到N个这样的坐标轴，我们取前k个去近似这个空间（选择的k个坐标轴能够使得空间的压缩使得数据的损失最小），这样就从一个N维的空间压缩到k维的空间了。

一般来说，方差大的方向是信号的方向，方差小的方向是噪声的方向，我们在数据挖掘中或者数字信号处理中，往往要提高信号与噪声的比例，也就是信噪比。故上图选择方差大的signal方向就能对原数据获得较好的近似。

---

 

假设我们矩阵每一行表示一个样本，每一列表示一个feature，用矩阵的语言来表示，将一个m * n的矩阵A的进行坐标轴的变化，P就是一个变换的矩阵从一个N维的空间变换到另一个N维的空间，在空间中就会进行一些类似于旋转、拉伸的变化。

而将一个m * n的矩阵A变换成一个m * r的矩阵，这样就会使得本来有n个feature的，变成了有r个feature了（r < n)，这r个其实就是对n个feature的一种提炼，我们就把这个称为feature的压缩。即：

但是这个怎么和SVD扯上关系呢？之前谈到，SVD得出的奇异向量也是从奇异值由大到小排列的，按PCA的观点来看，就是方差最大的坐标轴就是第一个奇异向量，方差次大的坐标轴就是第二个奇异向量…观察用于近似原数据的SVD式子：

在矩阵的两边同时乘上一个矩阵V，由于V是一个正交的矩阵，所以V转置乘以V得到单位阵I，所以可以化成后面的式子

将与上面的进行对比，在这里，其实V就是P，也就是一个变化的向量。这里是将一个m * n 的矩阵压缩到一个m * r的矩阵，也就是对列进行压缩（对feature进行压缩）

 

若想对行进行压缩（在PCA的观点下，对行进行压缩可以理解为，将一些相似的sample合并在一起，或者将一些没有太大价值的sample去掉）同样我们写出一个通用的行压缩例子：

这样就从一个m行的矩阵压缩到一个r行的矩阵了，对SVD来说也是一样的，我们对SVD分解的式子两边乘以U的转置U'

 

也就是说，SVD的左奇异矩阵可以用于行数的压缩。相对的，右奇异矩阵可以用于列数即特征维度的压缩

 

2.潜在语义索引（LSI）：

潜在语义索引LSI，有的文章也叫LSA，和传统向量空间模型(vector space model)一样使用向量来表示词(terms)和文档(documents)，并通过向量间的关系(如夹角)来判断词及文档间的关系；不同的是，LSI将词和文档映射到潜在语义空间，从而去除了原始向量空间中的一些“噪音”，提高了信息检索的精确度。

在自然语言处理中采用SVD方法，则有：

• 第一个矩阵U中的每一行表示意思相关的一类词，其中的每个非零元素表示这类词中每个词的重要性（或者说相关性），数值越大越相关。

• 第三个矩阵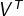中的每一列表示同一主题一类文章，其中每个元素表示这类文章中每篇文章的相关性。

• 第二个矩阵Σ则表示类词和文章之间的相关性。因此，我们只要对关联矩阵A进行一次奇异值分解，我们就可以同时完成了近义词分类和文章的分类。（同时得到每类文章和每类词的相关性）

 

例：

如图的一个矩阵，一行表示一个词在哪些title中出现了，一列表示一个title中有哪些词，比如T1这title中就有guide、investing、market、stock四个词，各出现了一次（我们平常的矩阵一般是行代表一个样本，列代表一个特性。这里的每一行相当于一个一维特征，每一列相当于一个样本的转置，这样只会影响我们的SVD左右奇异向量产生意义上的变化而不会影响计算)

对这个矩阵进行SVD，得到如下矩阵：

左奇异向量表示词的一些特性，右奇异向量表示文档的一些特性，中间的奇异值矩阵表示左奇异向量的一行与右奇异向量的一列的重要程度，数字越大越重要。

继续看这个矩阵还可以发现一些有意思的东西，首先，左奇异向量的第一列表示每一个词的出现频繁程度，虽然不是线性的，但是可以认为是一个大概的描述，比如book是0.15对应文档中出现的2次，investing是0.74对应了文档中出现了9次，rich是0.36对应文档中出现了3次；

其次，右奇异向量中一的第一行表示每一篇文档中的出现词的个数的近似，比如说，T6是0.49，出现了5个词，T2是0.22，出现了2个词。

 

然后我们反过头来看，我们可以将左奇异向量和右奇异向量都取后2维（之前是3维的矩阵），投影到一个平面上，可以得到：

在图上，每一个红色的点，都表示一个词，每一个蓝色的点，都表示一篇文档，这样我们可以对这些词和文档进行聚类，比如说stock 和 market可以放在一类，因为他们老是出现在一起，real和estate可以放在一类，dads，guide这种词就看起来有点孤立了，我们就不对他们进行合并了。按这样聚类出现的效果，可以提取文档集合中的近义词，这样当用户检索文档的时候，是用语义级别（近义词集合）去检索了，而不是之前的词的级别。这样一减少我们的检索、存储量，因为这样压缩的文档集合和PCA是异曲同工的，二可以提高我们的用户体验，用户输入一个词，我们可以在这个词的近义词的集合中去找，这是传统的索引无法做到的。

 

三、SVD应用实例：推荐系统

如上一样的用户评分矩阵，每一列代表一个user，每一行代表一个item，矩阵值代表user对item的评分。

对该矩阵进行SVD分解，k取2来近似原数据矩阵

 其中U矩阵每一行代表item的一些特性，V矩阵的转置（图中有误，图上的是V而不是V的转置）每一列代表着user的一些特性

 把U矩阵的第一列值作为x，第二列值作为y，V矩阵也是如此，作出下图：

从图中可以看出:Season5，Season6特别靠近。Ben和Fred也特别靠近。同时我们仔细看一下A矩阵可以发现，A矩阵的第5行向量和第6行向量特别相似，Ben所在的列向量和Fred所在的列向量也特别相似。

 

假设现在有个名字叫Bob的新用户，并且已知这个用户对season n的评分向量为：[5 5 0 0 0 5]。（此向量为列向量）。对该用户进行个性化推荐首先我们先找到与Bob相似的用户。

画在图上的是二维向量，故我们先对Bob的评分向量进行降维：

 （上图中第二行式子有错误，Bob的转置应为行向量）

 

采用余弦相似度计算相似，可以算出Bob与Ben相似。

观察Ben的评分向量：【5 5 3 0 5 5】

对比Bob的评分向量：【5 5 0 0 0 5】

一种简单的推荐策略是找出ben评分过而Bob未评分的item，进行预测评分并排序，然后选出前k个推荐。

改进推荐策略：找出多个相似用户，根据相似度作为权重进行预测评分

 

 

参考文章

（1）SVD在推荐系统中的应用

（2）奇异值分解(SVD)原理与在降维中的应用

（3）机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用

（4）奇异值分解(SVD) --- 线性变换几何意义

（5）奇异值分解(SVD) --- 几何意义