【Algorithm&DataStructure】极客时间-数据结构与算法之美专栏笔记I
以下内容均来自本人学习专栏时的个人笔记、总结,侵权即删
专栏地址:https://time.geekbang.org/column/126
希望看到本文章的,可以去支持一下老师,讲的很好!!
目录
时间复杂度为O(n)=logn的代码
没有头结点要多判断什么?-->哨兵结点作用
数组和链表的区别
容器(ArrayList)和数组的选择
队列
阻塞队列
并发队列
队列的应用场景和实现方式选择
递归
递归需要满足的三个条件
如何编写递归
递归注意事项
警惕堆栈溢出(空间复杂度高)
警惕重复计算
排序
O(n^2)的排序(基于比较)
冒泡排序
插入排序
选择排序
O(nlogn)的排序(基于比较)
归并排序(分治思想=大问题化成小问题)(递归编程技巧)
快排
O(n)的排序(非基于比较,对数据要求苛刻,复杂度n-》线性排序)
桶排序
计数排序(桶排序的一种特殊情况)
基数排序(排序低位-->排序高位)
二分查找(O(logn))
二分查找变体
思考题1(LeetCode33)
思考题2(求一个数平方根,小数点精确到后六位)
跳表(区间查询)[链表中的二分查找]{Redis-->散列表+跳表}
|S:O(logn) K:O(n)|
跳表索引的动态更新:
为什么Redis用跳表不用红黑树
散列表(高效的CRUD)
核心
散列表哈希冲突的解决方法
开放寻址法(不允许在同一个结点)
链表法(允许在同一个结点)
如何设计一个散列表
为什么散列表和链表经常一块使用(顺序遍历)
哈希算法的分布式应用
负载均衡
数据分片
分布式存储
时间复杂度为O(n)=logn的代码
i = 1;
while(n变量 i 的取值就是一个等比数列。如果我把它一个一个列出来,就应该是这个样子的:
所以,只需要知道x的值,就可以知道这段代码执行的次数了,也就是log2n
而对于 i = i × x 的情况(x是一个常数,可以想成3),也可以得知时间复杂度是logxn
而所有对数阶的时间复杂度一般都表示为logn,因为可以通过换底公式,logxn = logx2 × log2n(x是一个常数)
平均时间复杂度=单一情况发生的概率 × 这种情况的时间复杂度
--->>>均摊时间复杂度(思维角度):O(1)->O(1)->O(1)->O(1)->...n次...->O(n) :执行n次O(1)后会有一次O(n)的操作
可以将O(n)分成n次均摊到每个O(1)的操作,这样算下来整个代码的平均时间复杂度也就是O(1)了
没有头结点要多判断什么?-->哨兵结点作用
/*
* 没有头结点的插入、删除
*/
//一般插入结点
new_node->next = p->next;
p->next = new_node;
//空链表第一个结点
if (head == null) {
head = new_node;
}
//删除结点
p->next = p->next->next;
//空链表最后一个结点删除
if (head->next == null) {
head = null;
}
如果有头结点(不存数据的结点),不管有没有结点都可以使用同一个逻辑了,不用再根据特殊情况来判断
数组和链表的区别
这里我要特别纠正一个“错误”。我在面试的时候,常常会问数组和链表的区别,很多人都回答说,“链表适合插入、删除,时间复杂度 O(1);数组适合查找,查找时间复杂度为 O(1)”。实际上,这种表述是不准确的。数组是适合查找操作,但是查找的时间复杂度并不为 O(1)。即便是排好序的数组,你用二分查找,时间复杂度也是 O(logn)。所以,正确的表述应该是,数组支持随机访问,根据下标随机访问的时间复杂度为 O(1)。
容器(ArrayList)和数组的选择
我个人觉得,ArrayList 最大的优势就是可以将很多数组操作的细节封装起来。比如前面提到的数组插入、删除数据时需要移其他数据等。另外,它还有一个优势,就是支持动态扩容。
- Java ArrayList 无法存储基本类型,比如 int、long,需要封装为 Integer、Long 类,而 Autoboxing、Unboxing 则有一定的性能消耗,所以如果特别关注性能,或者希望使用基本类型,就可以选用数组。
- 如果数据大小事先已知,并且对数据的操作非常简单,用不到 ArrayList 提供的大部分方法,也可以直接使用数组。
- 还有一个是我个人的喜好,当要表示多维数组时,用数组往往会更加直观。比如 Object[][] array;而用容器的话则需要这样定义:ArrayList
array
队列
阻塞队列
其实就是在队列基础上增加了阻塞操作。简单来说,就是在队列为空的时候,从队头取数据会被阻塞。因为此时还没有数据可取,直到队列中有了数据才能返回;如果队列已经满了,那么插入数据的操作就会被阻塞,直到队列中有空闲位置后再插入数据,然后再返回。
你应该已经发现了,上述的定义就是一个“生产者 - 消费者模型”!是的,我们可以使用阻塞队列,轻松实现一个“生产者 - 消费者模型”!
并发队列
前面我们讲了阻塞队列,在多线程情况下,会有多个线程同时操作队列,这个时候就会存在线程安全问题,那如何实现一个线程安全的队列呢?
最简单直接的实现方式是直接在 enqueue()、dequeue() 方法上加锁,但是锁粒度大并发度会比较低,同一时刻仅允许一个存或者取操作。实际上,基于数组的循环队列,利用 CAS 原子操作,可以实现非常高效的并发队列。这也是循环队列比链式队列应用更加广泛的原因。在实战篇讲 Disruptor 的时候,我会再详细讲并发队列的应用。
队列的应用场景和实现方式选择
队列的知识就讲完了,我们现在回过来看下开篇的问题。线程池没有空闲线程时,新的任务请求线程资源时,线程池该如何处理?各种处理策略又是如何实现的呢?我们一般有两种处理策略。
第一种是非阻塞的处理方式,直接拒绝任务请求;另一种是阻塞的处理方式,将请求排队,等到有空闲线程时,取出排队的请求继续处理。那如何存储排队的请求呢?我们希望公平地处理每个排队的请求,先进者先服务,所以队列这种数据结构很适合来存储排队请求。我们前面说过,队列有基于链表和基于数组这两种实现方式。
这两种实现方式对于排队请求又有什么区别呢?基于链表的实现方式,可以实现一个支持无限排队的无界队列(unbounded queue),但是可能会导致过多的请求排队等待,请求处理的响应时间过长。所以,针对响应时间比较敏感的系统,基于链表实现的无限排队的线程池是不合适的。而基于数组实现的有界队列(bounded queue),队列的大小有限,所以线程池中排队的请求超过队列大小时,接下来的请求就会被拒绝,这种方式对响应时间敏感的系统来说,就相对更加合理。不过,设置一个合理的队列大小,也是非常有讲究的。队列太大导致等待的请求太多,队列太小会导致无法充分利用系统资源、发挥最大性能。实际上,对于大部分资源有限的场景,当没有空闲资源时,基本上都可以通过“队列”这种数据结构来实现请求排队。
递归
递归需要满足的三个条件
- 一个问题的解可以分解为几个子问题的解
- 这个问题与分解之后的子问题,除了数据规模不同,求解思路完全一样
- 存在递归终止条件
如何编写递归
写出递归公式,找到终止条件,将两者转换成代码
递归注意事项
警惕堆栈溢出(空间复杂度高)
递归调用一次就会在内存栈中保存一次现场数据,所以在分析递归复杂度的时候要考虑这个部分,同时也要考虑递归层数过深导致的堆栈溢出。
解决方法:
- 方法①:在比如说递归深度超过1000层的时候就抛出异常,不再进行递归(规模小的时候适用,因为实时计算栈的剩余空间过于复杂)
- 方法②:自己模拟一个栈,用非递归代码实现
警惕重复计算
排序
O(n^2)的排序(基于比较)
冒泡排序
/**
* 冒泡排序
* @param a
*/
private static void bubbleSortLineryArray(int[] a) {
for(int i=0;i a[j+1]) {
int tmp = a[j];
a[j] = a[j+1];
a[j+1] = tmp;
flag = true;
}
}
if(!flag)break;
}
}
有序度、逆序度
满有序度:完全有序的数组的有序度
逆序度的定义正好跟有序度相反(默认从小到大为有序)
插入排序
将数据分为两个区间:已排序区间和未排序区间
/**
* 插入排序
* @param a
*/
private static void insertSortLineryArray(int[] a) {
for(int i=1;i=0;j--) {
if(a[j] > value) {
a[j+1] = a[j];
}else {
break; //此时a[j+1]就是value要放的地方,a[j+1]的值在上个循环已经移动到a[j+2]了
}
}
a[j+1] = value;
}
} 选择排序
/**
* 选择排序,每次选择最小的交换位置
* @param a
*/
private static void selectSortLineryArray(int[] a) {
for(int i=0;ia[j]) {
min = a[j];
b = j; //要记录最小值的位置,然后来交换
}
}
int tmp = a[i];
a[i] = min;
a[b] = tmp;
}
}
O(nlogn)的排序(基于比较)
归并排序(分治思想=大问题化成小问题)(递归编程技巧)
如果要排序一个数组,我们先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排序好的两部分合并在一起。就可以得到一个有序的数组了。
*时间复杂度求解:
我们假设对 n 个元素进行归并排序需要的时间是 T(n),那分解成两个子数组排序的时间都是 T(n/2)。我们知道,merge() 函数合并两个有序子数组的时间复杂度是 O(n)。所以,套用前面的公式,归并排序的时间复杂度的计算公式就是:
T(1) = C; n=1 时,只需要常量级的执行时间,所以表示为 C。
T(n) = 2*T(n/2) + n; n>1
通过这个公式,如何来求解 T(n) 呢?还不够直观?那我们再进一步分解一下计算过程。
T(n) = 2*T(n/2) + n
= 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2*n
= 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n
= 8*(2*T(n/16) + n/8) + 3*n = 16*T(n/16) + 4*n
......
= 2^k * T(n/2^k) + k * n
......
通过这样一步一步分解推导,我们可以得到 T(n) = 2^kT(n/2^k)+kn。
当 T(n/2^k)=T(1) 时,也就是 n/2^k=1,我们得到 k=log2n 。
我们将 k 值代入上面的公式,得到 T(n)=Cn+nlog2n 。如果我们用大 O 标记法来表示的话,T(n) 就等于 O(nlogn)。所以归并排序的时间复杂度是 O(nlogn)。
快排
快排的思想是这样的:
- 如果要排序数组中下标从 p 到 r 之间的一组数据,我们选择 p 到 r 之间的任意一个数据作为 pivot(分区点)。
- 我们遍历 p 到 r 之间的数据,将小于 pivot 的放到左边,将大于 pivot 的放到右边,将 pivot 放到中间。经过这一步骤之后,数组 p 到 r 之间的数据就被分成了三个部分,前面 p 到 q-1 之间都是小于 pivot 的,中间是 pivot,后面的 q+1 到 r 之间是大于 pivot 的。
- 根据分治、递归的处理思想,我们可以用递归排序下标从 p 到 q-1 之间的数据和下标从 q+1 到 r 之间的数据,直到区间缩小为 1,就说明所有的数据都有序了。
private static void quickSortLineryArray(int[] a, int start, int end) {
if(a.length == 0 || a.length == 1) {
return ;
}
int i = start;
int j = start; //j负责检查小于key的
int key = a[end];
while(j < end){
if(a[j] < key) {
int tmp = a[i];
a[i] = a[j];
a[j] = tmp;
i++;
}
j++;
}
int tmp = a[i];
a[i] = a[end];
a[end] = tmp;
if(i > start)quickSortLineryArray(a, start, i-1);
if(i < end)quickSortLineryArray(a, i+1, end);
}
*快排的优化:
快排在最坏的条件下(每次分区点都选择最后一个数据),时间复杂度会退化O(n^2)
所以快排的优化核心就在对于分区点的选择
**常用、简单的分区算法:
- 三数取中法:从区间的首、尾、中间分别取出一个数,然后比较大小,取这三个数的中间值作为分区点。可以根据排序数组的规模来上升为“五数取中”或者“十数取中”
- 随机法:随机选择一个元素作为分区点,看运气
O(n)的排序(非基于比较,对数据要求苛刻,复杂度n-》线性排序)
桶排序
*数据要求:
- 首先,要排序的数据需要很容易就能划分成 m 个桶,并且,桶与桶之间有着天然的大小顺序。这样每个桶内的数据都排序完之后,桶与桶之间的数据不需要再进行排序。
- 其次,数据在各个桶之间的分布是比较均匀的。如果数据经过桶的划分之后,有些桶里的数据非常多,有些非常少,很不平均,那桶内数据排序的时间复杂度就不是常量级了。在极端情况下,如果数据都被划分到一个桶里,那就退化为 O(nlogn) 的排序算法了。
*适用场景:
桶排序比较适合用在外部排序中。所谓的外部排序就是数据存储在外部磁盘中,数据量比较大,内存有限,无法将数据全部加载到内存中。
计数排序(桶排序的一种特殊情况)
*原理:
①准备:两个数组:
- A:存放数据在不同下标(可以看做桶,下标值是数据的值)对应的个数(所谓“计数”)(数组大小是原数组数据数值个数)
==转换成==> 当前桶在已排好序数组中的位置(下标号),用求和的方式(A[k]存储小于等于数值k的数据个数)
- B:用于存放已排好序的数据的数组(同原数组大小相同)
②移动:每向B添加一个数据,A中对应下标数据上的值就-1(也就是个数少了一个,因为被分配了)
*适用场景&限制:
计数排序只能用在数据范围(数组A的大小)不大的场景,如果数据范围 k 比要排序的数据 n 大很多,就不适合用计数排序了。
而且,计数排序只能给非负整数排序,如果要排序的数据时其他类型的,要将其不改变相对大小的情况下,转换成非负整数。
基数排序(排序低位-->排序高位)
*数据要求:
数据需要可以分割出独立的“位”来比较(比如十分位、百分位),而且位之间有递进的关系(十分位比百分位弱),如果a的数据的高位比b数据大,那剩下的低位就不用比较了。除此之外,每一位的数据范围不能太大,要可以用线性排序算法来排序(算法必须是稳定的,否则低位的排序就没有意义了),否则基数排序的时间复杂度就无法做到O(n)了。
排序算法的实现
O(n^2)不一定就是比O(nlogn)执行的时间要长,因为大O时间复杂度一般都省去了某些参数,而这些参数在小规模数据时的作用是不同的。所以对于小规模的数据,有时可以考虑一下复杂度O(n^2)的排序算法
【Java】Collection.sort()的实现:
二分查找(O(logn))
着重掌握它的三个容易出错的地方:
- 循环退出条件[ while( low <= high) , <的话可能会错过最后一次循环时low或者high等于value]
- mid的取值
- low 和 high 的更新
实际上,mid=(low+high)/2 这种写法是有问题的。因为如果 low 和 high 比较大的话,两者之和就有可能会溢出。改进的方法是将 mid 的计算方式写成 low+(high-low)/2。更进一步,如果要将性能优化到极致的话,我们可以将这里的除以 2 操作转化成位运算 low+((high-low)>>1) [外层括号不能省,优先级问题]。因为相比除法运算来说,计算机处理位运算要快得多。
那二分查找能否依赖其他数据结构呢?比如链表。答案是不可以的,主要原因是二分查找算法需要按照下标随机访问元素。我们在数组和链表那两节讲过,数组按照下标随机访问数据的时间复杂度是 O(1),而链表随机访问的时间复杂度是 O(n)。所以,如果数据使用链表存储,二分查找的时间复杂就会变得很高。
虽然大部分情况下,用二分查找可以解决的问题,用散列表、二叉树都可以解决。但是,我们后面会讲,不管是散列表还是二叉树,都会需要比较多的额外的内存空间。如果用散列表或者二叉树来存储这 1000 万的数据,用 100MB 的内存肯定是存不下的。而二分查找底层依赖的是数组,除了数据本身之外,不需要额外存储其他信息,是最省内存空间的存储方式,所以刚好能在限定的内存大小下解决这个问题。
二分查找变体
①查找第一个值等于给定值的元素
/**
* 查找第一个值等于给定定值的元素
*/
private static int FirstEqualConst(int[] a, int value) {
int low = 0;
int high = a.length-1;
while(low <= high) {
int mid = low + ((high - low) >> 1);
if(a[mid] > value) {
high = mid - 1;
}else if(a[mid] < value) {
low = mid + 1;
}else {
if((mid == 0) || (a[mid - 1] != value))return mid;
high = mid - 1;
}
}
return -1;
}②查找最后一个值等于给定值的元素
/**
* 查找最后一个值等于给定定值的元素
*/
private static int LastEqualConst(int[] a, int value) {
int low = 0;
int high = a.length - 1;
while(low <= high) {
int mid = low + ((high - low) >> 1);
if(a[mid] > value) {
high = mid - 1;
}else if(a[mid] < value) {
low = mid + 1;
}else {
if(mid == a.length-1 || a[mid + 1] != value)return mid;
low = mid + 1;
}
}
return -1;
}③查找第一个大于等于给定值的元素
/**
* 查找第一个值大于等于给定定值的元素
*/
private static int FirstGreaterEquConst(int[] a, int value) {
int low = 0;
int high = a.length - 1;
while(low <= high) {
int mid = low + ((high - low) >> 1);
if(a[mid] >= value) {
if(mid == 0 || a[mid - 1] < value)return mid;
high = mid - 1;
}else {
low = mid + 1;
}
}
return -1;
}④查找最后一个小于等于给定值的元素
/**
* 查找最后一个小于等于(最靠近)给定定值的元素
*/
private static int LastLessEquConst(int[] a, int value) {
int low = 0;
int high = a.length - 1;
while(low <= high) {
int mid = low + ((high - low) >> 1);
if(a[mid] <= value) {
if(mid == a.length - 1 || a[mid + 1] > value)return mid;
low = mid + 1;
}else {
high = mid - 1;
}
}
return -1;
}
思考题1(LeetCode33)
如果有序数组是一个循环有序数组,比如 4,5,6,1,2,3。针对这种情况,如何实现一个求“值等于给定值”的二分查找算法?
/**
* LeetCode-33-循环有序数组的二分查找
*/
private static int CircleArray(int[] a, int value) {
/*
* 想法:一次循环找到中间点,判断在哪个区间,复杂度O(n)
*/
int n = a.length;
//flag=0代表value在中间点左边,flag=1代表value在中间点右边
int flag = value >= a[0]? 0 : 1;
int max = n - 1 ; //max是数组最大值下标
int high,low;
for(int i=1;ia[i]) {
max = i-1;
break;
}
}
if(flag == 0) {
low = 0;
high = max;
while(low <= high){
int mid = low + ((high - low) >> 1);
if(a[mid] > value) {
high = mid - 1;
}else if(a[mid] < value) {
low = mid + 1;
}else {
return mid;
}
}
}else if(flag == 1) {
low = max + 1;
high = n - 1;
while(low <= high){
int mid = low + ((high - low) >> 1);
if(a[mid] > value) {
high = mid - 1;
}else if(a[mid] < value) {
low = mid + 1;
}else {
return mid;
}
}
}
return -1;
}
思考题2(求一个数平方根,小数点精确到后六位)
/**
* 精确到后六位的平方根
*/
private static Double sqrt(double x, double precision) {
double low = 0;
double high = x;
double mid = low + (high - low)/2;
while(high - low > precision) { //precision=0.00001
if(mid * mid > x) {
high = mid;
}else if(mid * mid < x) {
low = mid;
}else {
return mid;
}
mid = low + (high - low)/2;
}
return mid; //取出来的值还要进行额外处理,将六位后的数据消掉
}
跳表(区间查询)[链表中的二分查找]{Redis-->散列表+跳表}
|S:O(logn) K:O(n)|
具体实现:建立“索引”,以空间换时间
普通单链表查找一个数据的时间复杂度O(n)
而如果跳表每两个结点就抽出一个结点作为上一级索引的结点,第一级索引个数为n/2,第二级索引个数为n/4,排下来第k级索引个数就是n/2^k,而最高级的索引个数有两个结点,就可以推出级数k=log2n-1,而每一层最多遍历n+1个结点,所以在跳表中查找一个数的时间复杂度就是O(logn)
跳表索引的动态更新:
插入数据时,如果不更新索引,就可能出现两个索引结点之间数据非常多的情况,极端一点,可能退化成单链表
解决:在插入结点的同时将这个数据插入到部分索引层
为什么Redis用跳表不用红黑树
Redis中有序集合支持的核心操作:
- 插入一个数据
- 删除一个数据
- 查找一个数据
- 按照区间查找数据
- 迭代输出有序队列
其他四个的操作,红黑树也可以完成,时间复杂度和跳表一样。
但是按照区间查找数据,跳表可以做到O(logn)的时间复杂度来定位区间的起点,然后在原始链表中往后遍历就可以了。
其次,跳表相比红黑表容易实现+好懂(但是一般编程语言中Map类型都是通过红黑树实现)
散列表(高效的CRUD)
核心
散列函数设计和散列冲突解决
散列表哈希冲突的解决方法
开放寻址法(不允许在同一个结点)
- 线性探测:冲突后+一个常量,如果为空就插入,如果不为空就再加,一直到尾然后在从头加
- 二次探测:冲突后+一个常量^2,……
- 双重散列:冲突后换一个散列函数计算
链表法(允许在同一个结点)
如何设计一个散列表
- 一个合适的散列函数
- 装载因子阈值,设计动态扩容策略
过了阈值才扩容:使某次插入时间复杂度上升到O(n),因为要从原来的散列表搬移到新的散列表
一边插入一边搬:每插入一个数据就搬运一个原数据到新散列表
- 合适的散列冲突解决方法
开放寻址法:数据量、装载因子小(Java中的ThreadLocalMap)
链表法:数据量大,存放的对象大(这样就忽略链表中指针的内存消耗了)
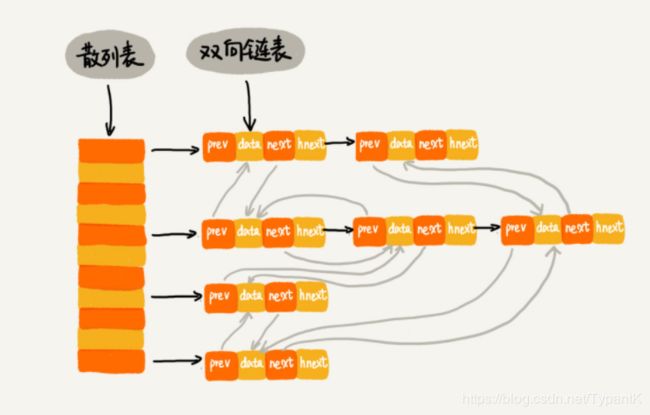
为什么散列表和链表经常一块使用(顺序遍历)
散列表支持非常高效的数据插入、删除、查找操作(O(1)),但散列表中的数据都是通过散列函数打乱之后无规律存储的。所以如果我们希望按照顺序来遍历数据,就要先取出数据到数组然后排序,这样效率就很低。但是如果结合链表的话,顺序问题就可以通过维护链表结点的next指针来实现了。
其中next是指向插入顺序上的下一个结点,而hnext是指向哈希冲突的下一个结点
Java中的LinkedHashMap也是这种结构(Linked并不是指链表法解决哈希冲突,而是双向链表)
哈希算法的分布式应用
负载均衡
实现会话粘滞(SessionSticky)[同一个客户端上,再一次会话中的所有请求都路由到同一个服务器上]
如果靠维护一张(客户端ip地址[会话id]+服务器编号映射)的表来实现的话,如果客户端很多会浪费内存空间。如果客户端下线、上线、服务器扩容、缩容都会导致映射失效,维护表成本很高。
我们可以通过哈希算法,对客户端 IP 地址或者会话 ID 计算哈希值,将取得的哈希值与服务器列表的大小进行取模运算,最终得到的值就是应该被路由到的服务器编号。这样,我们就可以把同一个 IP 过来的所有请求,都路由到同一个后端服务器上。
数据分片
将数据分成好几片存到不同机器
将每个数据中的关键字通过哈希函数计算哈希值,再跟机器的数量n取模,得到的值就是应存机器的编号(MapReduce基本思想)
分布式存储
数据分片后,机器数量不够需求,需要扩容时,所有数据关键字就要重新计算哈希值,然后来搬到新的机器=缓存中数据全部失效,客户端就是请求到数据库-->雪崩效应。
解决:一开始设计的时候,将所有的缓存槽连成一个环(一致性哈希--环形存储)[Redis集群]
https://www.sohu.com/a/158141377_479559
node相当于机器,key所在位置就是算出来的哈希值。key顺时针归属于node
为了防止,大部分key归属到一个node,提出了“虚拟结点”
简单来说就是将node拆分成好几个