2019开源论文|基于图神经网络的协同过滤算法
目录
- 引言
- 模型
- Embedding Layer
- Embedding Propagation Layers
- Model Prediction
- 实验
- 结论
引言
协同过滤——推荐算法
基本假设:相似的用户对物品展现出相似的偏好
包括两个部分:
1.embedding,即如何将user和item转化成向量表示;
2.interaction modeling,即如何基于user和item的表示来重建他们的历史交互。
传统协同过滤算法(如经典的矩阵分解和神经矩阵分解)本质还是给user和item初始化一个embedding,然后利用交互信息来优化模型。但是两者是异步的,并没有进行联系,即先embedding,再优化,并没有把交互信息编码进embedding中,所以这些embedding都是次优的。
如果可以将user-item的交互信息编码进embedding中,将提升embedding的表示能力,进而提升模型的预测能力。本文的主要创新点在与利用二部图神将网络将user-item的历史交互信息编码进embedding进而提升推荐模型效果。更重要的是,本文显式的考虑user-item之间的高阶连接性来进一步提升embedding的表示能力。

图 1 展示了一个 user-item 的二部图及 u1 的高阶连接性。u1 的高阶连接性表示 u1 通过长度大于 1 的路径连接到的节点。例如,u1 通过长度 l=2 的路径连接到 u2 和 u3,这代表 u1 的 2 阶连接性;u1 通过长度 l=3 的路径连接到 i4,i5,这代表 u1 的 3 阶连接性。需要注意的是,虽然 i4 和 i5 都是 u1 的 3 阶邻居,但是 i4 可以通过更多的路径连接到 u1,所以 i4 与 u1 的相似度更高。
模型
模型主要分为 3 个部分:1)Embedding Layer:将 user 和 item 的 ID 映射为向量表示;2)Embedding Propagation Layers:将初始的 user 和 item 表示基于图神经网络来更新;3)Prediction:基于更新后的 user 和 item 表示来进行预测。模型架构图见 Figure 2。
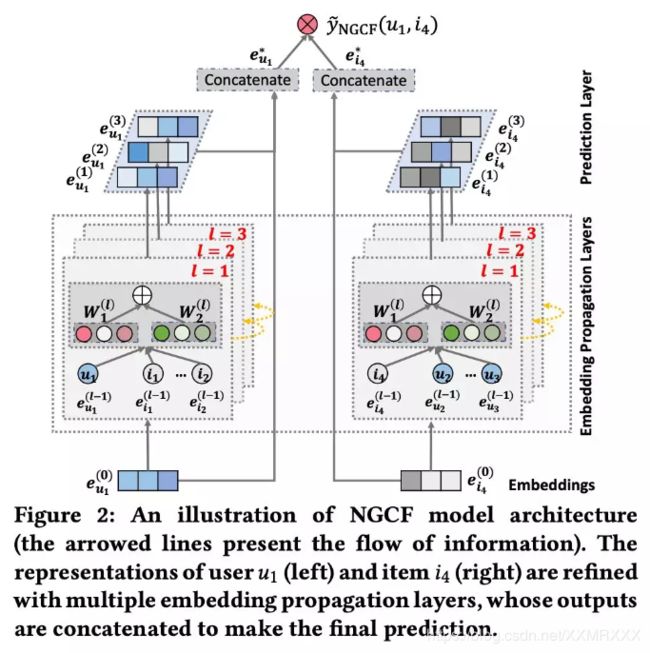
Embedding Layer
这里对 User 和 Item 分别初始化相应的 Embedding Matrix,然后通过 User 或者 Item 的 ID 进行 Embedding Lookup 将它们映射到一个向量表示。
 (1)
(1)
注意,这里初始化的 Embedding 可以认为是 0 阶表示,即 e u ( 0 ) = e u a n d e i ( 0 ) = e i e_u^{(0)}=e_u and e_i^{(0)} =e_i eu(0)=euandei(0)=ei
Embedding Propagation Layers
受 GNN 的 message-passing 架构的启发,NGCF 针对 User-Item 二部交互图设计了 Embedding Propagation 来学习 User 和 Item 的表示。这里作者首先详细的描述了一阶传播,然后泛化到高阶传播。
一阶传播主要包含:消息构建和消息聚合。给定(u,i),从 i 传播到 u 的消息 m u ← i m_{u \larr i} mu←i可以定义为:
m u ← i = f ( e i , e u , p u i ) ( 2 ) m_{u\larr i}=f(e_i,e_u,p_{ui})(2) mu←i=f(ei,eu,pui)(2)
m u ← i = 1 ∣ N u ∣ ∣ N i ∣ ( W 1 e i + W 2 ( e i ⊙ e u ) ) ( 3 ) m_{u\larr i}=\frac{1}{\sqrt{|N_u||N_i|}}(W_1e_i+W_2(e_i\odot e_u))(3) mu←i=∣Nu∣∣Ni∣1(W1ei+W2(ei⊙eu))(3)
其中, W 1 , W 2 ∈ R d ′ ∗ d W_1,W_2\in R^{d'*d} W1,W2∈Rd′∗d都是可学习的参数矩阵, N u N_u Nu和 N t N_t Nt分别代表 u 和 i 的度。这里 1 ∣ N u ∣ ∣ N i ∣ \frac{1}{\sqrt{|N_u||N_i|}} ∣Nu∣∣Ni∣1可以理解为归一化系数。
基于上面构建的消息,下一步就是聚合消息来更新节点表示:
e u ( 1 ) = L e a k y R e L U ( m u ← u + ∑ i ∈ N u m u ← i ) ( 4 ) e_u^{(1)}=LeakyReLU(m_{u\larr u}+\sum_{i\in N_u} m_{u\larr i}) (4) eu(1)=LeakyReLU(mu←u+i∈Nu∑mu←i)(4)
其中, e u ( 1 ) e_u^{(1)} eu(1)代表经过 1 次聚合之后的节点表示。因为单层的消息聚合只能聚合 1 阶邻居的信息,所以这里实际代表了 u 的一阶表示。需要注意的是,这里除了聚合邻居的信息,更重要的是考虑节点自身的信息 m u ← u = W 1 e u m_{u\larr u=W_1e_u} mu←u=W1eu。
高阶传播实际就是将上述的一阶传播堆叠多层。这样经过 l 次聚合,每个节点都会融合其 l 阶邻居的信息,也就得到了节点的 l 阶表示 e u ( l ) e_u^{(l)} eu(l)。
e u ( l ) = L e a k y R e L U ( m u ← u ( l ) + ∑ i ∈ N u m u ← i ) ( 5 ) e_u^{(l)}=LeakyReLU(m_{u\larr u}^{(l)}+\sum_{i\in N_u} m_{u\larr i})(5) eu(l)=LeakyReLU(mu←u(l)+i∈Nu∑mu←i)(5)
Figure 3 清晰地展示了如何在高阶传播中融合高阶邻居的信息。

上面的传播过程也可以写成矩阵的形式,这样在代码实现的时候可以高效的对节点 Embedding 进行更新。

其中, E ( l ) ∈ R ( N + M ) ∗ d l E^{(l)}\in R^{(N+M)*d_l} E(l)∈R(N+M)∗dl是 l 阶的 user 和 item 的表示, R ∈ R N ∗ M R\in R^{N*M} R∈RN∗M是 user-item 交互矩阵,D 是对角度矩阵。
Model Prediction
模型的预测非常简单,将 L 阶的节点表示分别拼接起来作为最终的节点表示,然后通过内积进行预测。
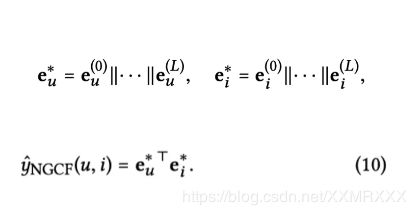
实际这里采用了类似 18 ICML Representation Learning on Graphs with Jumping Knowledge Networks 的做法来防止 GNN 中的过平滑问题。GNN 的过平滑问题是指,随着 GNN 层数增加,GNN 所学习的 Embedding 变得没有区分度。过平滑问题与本文要捕获的高阶连接性有一定的冲突,所以这里需要在克服过平滑问题。
实验
本文在 Gowalla、Yelp2018 和 Amazon-Book 上进行了大量实验来回答以下 3 个问题:
1.和 state-of-the-art 的方法相比,NGCF 的效果如何?
2.模型对于超参数(如模型层数,dropout)的敏感性。
3.高阶连接性对于模型的影响。
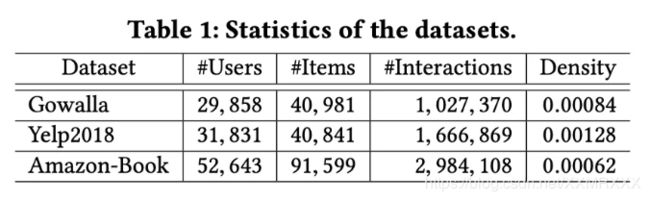
本文的 baseline 主要可以分为两大类:非图神经网络的推荐算法(如 MF 和 CMN)和基于图神经网络的推荐算法(PinSage 和 GC-MC)。实验效果如 Table 2 所示:

可以看出,本文所提出的 NGCF 优势很明显,尤其是在 recall 上的提升均超过 10%。同时,作者还对数据进行了稀疏化并进一步验证来说明 NGCF 来稀疏数据上的优势。

从 Figure 4 可以看出,NGCF 在数据稀疏度较高的时候有明显优势,随着稀疏度的下降,NGCF 的优势越来越小甚至被 baseline 超过了。
另外,作者验证了模型层数、卷积形式和 dropout 对 NGCF 的影响,具体见 Table 3、Table 4 和 Figure 5。


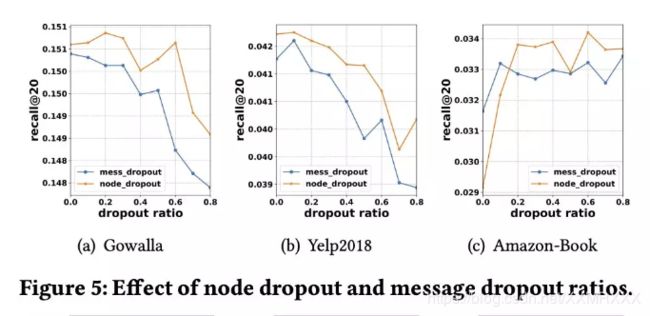
最后,作者研究了高阶连接性对 NGCF 的影响,如 Figure 6 所示。

注意这里 MF 可以看做是 NGCF-0。可以看出,随着阶数的增加,相同颜色的节点更好的聚集在一起。也就是说,高阶连接性确实有助于学习 User 和 Item 的 Embedding。
结论
本文提出了基于图神经网络的协同过滤算法 NGCF,它可以显式地将 User-Item 的高阶交互编码进 Embedding 中来提升 Embedding 的表示能力进而提升整个推荐效果。
NGCF 的关键就在于 Embedding Propagation Layer 来学习 User 和 Item 的 Embedding,后面的预测部分只是简单的内积。可以说,NGCF 较好地解决了协同过滤算法的第一个核心问题。
另外,本文的 Embedding Propagation 实际上没有考虑邻居的重要性,如果可以像 Graph Attention Network 在传播聚合过程中考虑邻居重要性的差异,NGCF 的效果应该可以进一步提升。
