Hash(散列表)算法实现原理
散列表
散列表,又叫做“哈希表”,它是基于高速存取的角度设计的,也是一种典型的“空间换时间”的做法。
散列表是依据关键码值(key)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中的一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组就叫做散列表。
哈希的思路很简单,如果所有的键都是整数,那么就可以使用一个简单的无序数组来实现:将键作为数组索引,值记为对应的值,这样就可以快速访问任意键的值。同样也可以扩展到更加复杂类型的键。
说明:在哈希表中,记录所在的位置与其关键字之间存在着一种确定的关系。只有这样我们才能预先知道所查关键字在表中的位置,从而直接通过下标查找记录,使ASL(查找成功时的平均查找长度)趋近于0.
(1)哈希函数是一个映射:即将关键字的集合映射到某个地址集合上,它的设置很灵活,只要这个地址集合的大小不超出允许的范围即可;
(2)哈希函数是一个压缩映射,因此,一般情况下很容易产生“冲突”现象。即key1 != kry2,但是 H(key1) = H(key2)
(3)只能尽量减少冲突而不能完全避免冲突,这是因为关键字集合比较大,其元素包括所有可能的关键字,而地址集合的元素比较少,近为哈希表中的地址。
1、哈希构造函数的方法
(1)直接定址法
取关键字或关键字的某个线性函数为Hash地址,即Hash(key)=key或者H(key) = a*key+b,其中a和b为常数。
此方法仅适合于:地址集合的大小等于关键字集合的大小。
(2)数字分析法
假设关键字是r进制数(如十进制数),并且Hash表中可能出现的关键字都是事先知道的,则可以选取关键字的若干数位或它们的组合作为Hash地址。选取的原则是使得到的Hash地址尽量避免冲突,即所选数位上的数字尽可能是随机的,分布均匀的。
此方法适用于:能预先估计出全体关键字的每一位上各种数字出现的频度
(3)平方取中法
取关键字平方后的中间几位作为Hash地址。通常在选定Hash函数的时候不一定能知道关键字的全部清空,仅取其中的几位为地址不一定合适,而一个数平方后的中间几位数和数的每一个数都相关,由此得到的Hash地址随机性更大,取的位数由表长决定。
此法适用于:关键字中的每一位都有某些数字重复出现频度很高的现象
(4)折叠法
将关键字分隔成若干部分,然后取它们的叠加和为Hash地址。叠加的方法有两种:移位叠加和边界叠加
移位叠加:将分割后的几部分低位对其相加
边界叠加:从一端沿分割线来回折叠,然后对其叠加
说明:所谓折叠法是将关键字分割成位数相同的几部分(最后一部分的位数可不同),然后取这几部分的叠加和(舍去进位),这种方法称为折叠法。适用于关键字位数较多,且关键字中每一位上数字分布大致均匀的情况。
举个例子:
当哈希表长度为1000时,允许的地址空间为三位十进制数,则对于关键字key = 101083318341991。
移位叠加 边界叠加
9 9 1 9 9 1
3 4 1 1 4 3
3 1 8 3 1 8
0 8 3 3 8 0
+ 1 0 1 1 0 1
——————————————————————
8 3 4 9 3 3
用移位叠加法得到的Hash地址为834,用边界叠加法得到的Hash地址为933。当然如果关键字不是数字而是字符串,可将其转换为数字(如利用ASCII字符),然后在用折叠法。
(5)除留余数法
取关键字被某个不大于Hash表表长m的数p除后所得的余数作为Hash地址,即Hash(key) = key mod p (p<=m)
p的选择很重要,一般p选择小于或者等于表长的最大素数,这样可以减少冲突。
例如,已知待散列元素为(18,75,60,43,54,90,46),表长m=10,p=7,则有
h(18)=18 % 7=4 h(75)=75 % 7=5 h(60)=60 % 7=4
h(43)=43 % 7=1 h(54)=54 % 7=5 h(90)=90 % 7=6
h(46)=46 % 7=4
此时冲突较多。为减少冲突,可取较大的m值和p值,如m=p=13,结果如下:
h(18)=18 % 13=5 h(75)=75 % 13=10 h(60)=60 % 13=8
h(43)=43 % 13=4 h(54)=54 % 13=2 h(90)=90 % 13=12
h(46)=46 % 13=7
(6)减去法
(7)基数转换法
(8)随机数法
(9)随机乘数法
(10)字符串数值哈希法
(11)旋转法
具体可参考:http://blog.csdn.net/tanggao1314/article/details/51457585
2、常用的Hash冲突处理方法
注意:这可能尽量减少冲突的发生,不可能完全避免冲突。因此,在建立Hash表的时候必须进行冲突处理。
(1)开放定址法
- 线性探查法:线性探查法是从发生冲突的地址(假设为d)开始,依次探查d的下一个地址(当到达下标为m-1的Hash表表尾时,下一个探查的地址就是表首地址0),直到找到一个空位置为止,当m>=n(n是表中关键字的个数)时,一定能找到一个空位置。
线性探查法的递推公式为 Hi(k) = (H(k)+i) Mod m (1<=i<=m-1)
线性探查法容易产生堆积问题。因为当连续出现若干个同义词后,设第一个同义词占用单元d,这连续的若干个同义词将占用d、d+1、d+2等单元,此时,随后任何d+1、d+2等单元上的Hash映射都会由于前面的同义词堆积而产生的冲突,尽管所有的这些关键字并没有同义词。
- 平方探查法:设发生冲突的地址为d,则用平方探查法所得到的新的地址为:d+1^2、d-1^2、d+2^2、d-2^2、..................平方探查法是一种较好的处理冲突的方法,可以避免出现堆积现象。缺点是不能探查Hash表上的所有单元,但至少能探查到一半的单元。
- 伪随机序列法
- 双Hash函数法
这种方法是同时构造多个不同的哈希函数:Hi=RH1(key) i=1,2,…,k当哈希地址Hi=RH1(key)发生冲突时,再计算Hi=RH2(key)……,直到冲突不再产生。这种方法不易产生聚集,但增加了计算时间。
(2)链地址法
这种方法的基本思想是将所有哈希地址为i的元素构成一个称为同义词链的单链表,并将单链表的头指针存在哈希表的第i个单元中,因而查找、插入和删除主要在同义词链中进行。链地址法适用于经常进行插入和删除的情况。
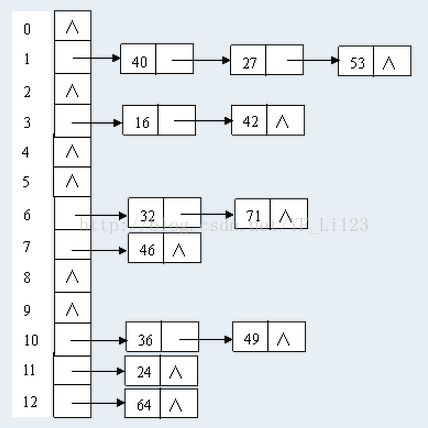
例如,已知一组关键字(32,40,36,53,16,46,71,27,42,24,49,64),哈希表长度为13,哈希函数为:H(key)= key % 13,则用链地址法处理冲突的结果如图
3、散列表的性能分析
查找成功时的平均查找长度(ASL1):指找到表中已有表项的平均次数,它是找到表中各个已有表项的平均比较次数。
查找不成功时的平均查找长度(ASL2):指在表中找不到待查的表项,但找到插入位置的平均比较次数,它是在表中所有可能散列到的地址上插入新元素时,为找到空位置而进行探查的平均次数。
装填因子:关键字个数/表长度
就拿上图中的例子来分别说明一下:
表1 关键字比较次数
|
关键字
|
32
|
40
|
36
|
53
|
16
|
46
|
71
|
27
|
42
|
24
|
49
|
64
|
|
比较次数
|
1
|
1
|
1
|
3
|
1
|
1
|
2
|
2
|
2
|
1
|
2
|
1
|
ASL1 = (1+1+1+3+1+1+1+2+2+2+1+2+1)/12 = 1.5
表2 地址比较次数
|
地址
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
|
比较次数
|
0
|
1
|
0
|
1
|
0
|
0
|
2
|
1
|
0
|
0
|
3
|
2
|
1
|
ASL2 = (1+1+2+1+3+2+1)/13 = 0.846
参考:http://blog.csdn.net/tanggao1314/article/details/51457585