利用异或判断二进制数中的1的个数的奇偶性
文章目录
- 异或压缩奇偶性信息
- 一位一位地异或
- 利用二叉树思想异或
- 关于有符号数和算术右移
- 利用x &= x-1求二进制1个数
- 利用逻辑右移求二进制1个数
- 两个二进制数异或后结果的1个数的奇偶性
异或压缩奇偶性信息
二进制数中的1的个数的奇偶性: 如果一个二进制数中的1的个数为奇数,那么返回1;如果为偶数,那么返回0。
给定二进制数01,它只有两位,那么它的奇偶性可以通过0^1 = 1获得,这里返回1,与它是奇数相符合。
给定二进制数11,它只有两位,那么它的奇偶性可以通过1^1 = 0获得,这里返回0,与它是偶数相符合。
总结:异或可以压缩两位上1个数的奇偶性。即压缩奇偶性信息为1或者0.
上面给出了两位的例子,下面给出四位的例子,以0111为例,它的1的个数为奇数,那么它的奇偶性就应该返回1。

利用压缩信息的规律,可以一步一步异或最终得出0111的奇偶性,过程如上,讲解如下:
1.开始异或是从左起第一个1开始的,因为第一个1左边只会是0,而它们对1的个数没有影响。
2.异或时,是需要保证异或的两个操作数所表示的压缩信息的范围是不重叠的:
(1)第一个异或操作中,左边操作数代表的是第2位的奇偶性,右边操作数代表的是第1位的奇偶性。
(2)第二个异或操作中,左边操作数代表的是第1,2位的奇偶性,右边操作数代表的是第0位的奇偶性。
3.异或应该到右起第一个1停止,这是最精确的做法,但到第0位停止是一种更为简单的判断方法。
总结:压缩后的奇偶性信息,可以继续和别的不重叠范围的奇偶性信息,进行进一步的压缩。

同样利用压缩信息的规律,但这里利用二叉树性质或者说归并思想,每次俩俩进行压缩信息,每行进行压缩时,当前行每个元素的奇偶性信息代表的范围都是前一行的2倍。
注意这里也满足,异或的两个操作数所表示的压缩信息的范围是不重叠的。
一位一位地异或
long fun_a(unsigned long x){
long val = 0;
while(x){
val ^= x;
x >>= 1;
}
return val & 0x1;
}
此代码的过程如本文图一所示,代码来自《深入理解计算机系统》练习题3.26。以x为0111为例分析程序:
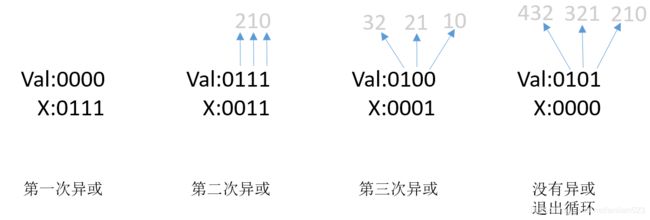
程序的运行过程如上图所示:
1.首先分析循环会执行几次,看while(x)和x >>= 1,所以将x的二进制中的左起第一个1移出去后,循环就会停止(此时x的二进制里面都是0),所以循环的次数为左起第一个1到第0位的长度。
2.x左起第一个1的索引位是2。每次异或的结果val中,从第2到第0位,每一位都代表着当前表示范围的奇偶性信息(上图箭头所指的灰色数字)。
3.当退出循环时,val的第0位就代表着第2到第0位的奇偶性信息了,所以最后通过val & 0x1取出第0位。
利用二叉树思想异或
bool OddOnes(int x)
{
x = x ^ (x >> 1);
x = x ^ (x >> 2);
x = x ^ (x >> 4);
x = x ^ (x >> 8);
x = x ^ (x >> 16);
return x & 1;
}
此代码的过程如本文图二所示。还是以x为0111为例分析程序:
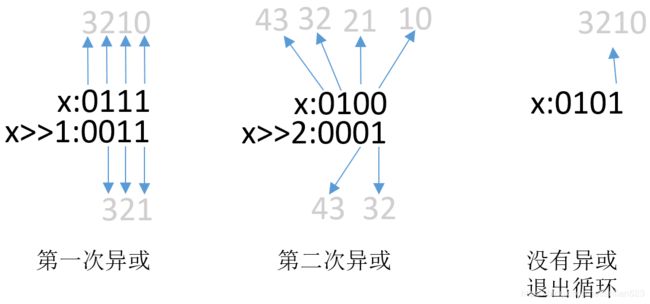
原代码的x是int型的即32位二进制。这里以x为4位二进制表示。
1.假设x为4位二进制,那么在x ^ (x >> 2)后就应该返回了。
2.如果x的二进制位数为w,那么应该执行 l o g 2 w log_2w log2w次x ^ (x >> n)的操作。因为int是32位,所以如上代码执行了5次。n从1开始,每次乘2。
3.最终,x的第0位,就会代表着从最高位到最低位范围的奇偶性信息。
4.上述代码看起来不是很优美,可以进行如下重构。
bool OddOnes(int x)
{
int max = sizeof(x) * 8;//获得x有多少位二进制位,这里是32
int n = 1;
while(n < max){
x = x ^ (x >> n);
n *= 2;
}
return x & 1;
}
关于有符号数和算术右移
直觉上讲,上述两种方法要是使用逻辑右移是肯定没有问题的。但到底使用算术右移还是逻辑右移是由编译器决定的,当编译器发现变量是无符号数时,使用逻辑右移;变量是补码数时,使用算术右移。
在方法利用二叉树思想异或中,虽然会使用到算术右移,但拓展出来的符号位并不会影响到最终第0位表示的范围。
同样的,在方法一位一位地异或中,也可以将变量x改成int型,原因如上。
可以想到,int型变量右移31位后,32位上的值将都会是符号位的值。
利用x &= x-1求二进制1个数
原理:一个二进制数减1,若右起第一个1的索引位置是m,那么从m到0位的二进制会逐位取反。所以,x &= x-1会使得从m到0位的二进制都会变成0。
示例:x is 0100,x-1 is 0011,x &= x-1后x = 0000。
bool OddOnes(int x)
{
int cnt = 0;
while(x)
{
cnt++;
x &= x-1;
}
return cnt & 1;//获得奇偶性
}
每执行一次x &= x-1就会去掉x二进制中的右起第一个1,当所有的1都被去掉后,循环停止,所以变量cnt记录了1的个数。
利用逻辑右移求二进制1个数
原理:就算传进来的是一个int型,直接转成unsigned int型就好,因为转换后位级表示不会变,且可以使用到逻辑右移了。但这个方法比较笨,需要从左起第一个1开始遍历到第0位,如果是负数那么符号位为1,那就惨了,得全部遍历了。
int count_one_bits(unsigned int n)//这里强行转换成无符号数
{
int count=0;
while(n)
{
if(n&1)
count++;
n=n>>1;
}
return count;
}
但是要注意转换类型大小要一致:
1)从大转到小,肯定不对。都截断了,除非被截断的部分一个1都没有,才可能返回正确结果。
2)从小转到大。如果本来实参是无符号数还好,拓展出来的位都是0,对结果没有影响。但如果实参是补码数且是负数,那么转换过程是,先拓展大小,再转换有无符号。在拓展大小时,使用的是符号拓展,所以就会莫名多出来好多1。
所以建议就是,最好保持转换类型大小,但上述代码并没有此项保证,读者可以自行优化。比如,变量如是单字节就转unsigned char;双字节就unsigned short;四字节就unsigned int;八字节就uint64_t(注意long在32位编译器也是4字节的哦,所以得用uint64_t);
两个二进制数异或后结果的1个数的奇偶性

假设数一和数二的二进制位数都为w位。数一有x个0,数二有y个0。我们需要关注的是,数一的0与数二的1的匹配、数二的0与数一的1的匹配。
1.首先假设数一中有k个0和数二的1匹配上了。所以会有k个1产生了。
2.那么数一中,剩下的x-k个0,就只能和数二的0匹配了。这里不会有1产生。
3.现在开始关注数二的0与数一的1的匹配,因为2步骤所以数二中的0能和1匹配的个数只有y-(x-k)了,因为12步骤中已经将数一中的0分配完了,所以数二剩下的y-(x-k)个0就只能和数一中的1的匹配了。这里产生y-(x-k)个1。
故异或结果的1的总个数为:k+y-(x-k)=2*k+y-x
且变量的二进制位数w必为偶数。
分为三种情况讨论:
1.拥有奇数个1的二进制数与拥有奇数个1的二进制数的异或运算:w为偶数,所以x,y均为奇数,此时y-x结果为偶数。
2.拥有奇数个1的二进制数与拥有偶数个1的二进制数的异或运算:同上,此时x为奇数,y为偶数,y-x结果为奇数。
3.拥有偶数个1的二进制数与拥有偶数个1的二进制数的异或运算:此时x为偶数,y为偶数,y-x为偶数或0.
【参考博客】:
[1] https://blog.csdn.net/luckyxiaoqiang/article/details/7249099
[2] https://blog.csdn.net/zhang_yang_43/article/details/72818933