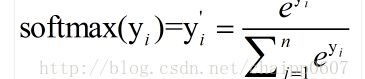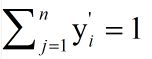交叉熵作为损失函数在神经网络中的作用和几种常用的交叉熵损失函数

交叉熵的作用

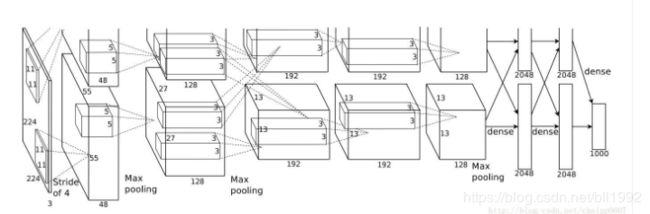
 通过神经网络解决分类问题时，最常用的一种方式就是在最后一层设置n个输出节点，无论在浅层神经网络还是在CNN中都是如此的，比如，在AlexNet中最后输出层有1000个节点。

一般情况下，最后一个输出层的节点个数与分类认为的目标数相等。假设最后节点数为N，那么对于每一个样例，神经网络可以得到一个N维的数组作为输出结果，数组中的每一个维度对应一个类别，在理想的情况下，如果一个样本属于k，那么这个类别所对应的输出节点的输出值应该是1，而其他节点的输出都为0，即[0,0,1,0,.......0,0],这个数组也就是赝本的label，是神经网络最期望输出的结果，交叉熵就是用来判断实际输出与期望输出的接近程度！它刻画的是两个概率分布之间的距离。

softmax回归原理

神经网络的原始输出不是一个概率值，实质上只是输入的数值做了复杂的加权和与非线性处理后的一个值而已，那么如何将这个输出变成一个概率分布呢？

这就是softmax层的作用，假设神经网络的原始输出为y1,y2,......yn,那么经过softmax回归处理后的输出为：

                      

             很显然的是：

                                           

而单个节点的输出变成一个概率值，经过softmax处理后结果作为神经网络最后的输出。

交叉熵的原理

交叉熵刻画的是实际输出（概率）与期望输出（概率）的距离，也就是交叉熵的值越小，两个概率分布就越近。假设概率分布p为期望输出，概率分布q为实际输出，H(p,q)为交叉熵，则：

                                      

这个公式如何表达距离呢，举个例子：

假设N=3，期望输出为p=(1,0,0)，实际输出q1=(0.5,0.2,0.3)，q2=(0.8,0.1,0.1)，那么：

                                   

很显然，q2与p更为接近，它的交叉熵也更小。 除此之外，交叉熵还有另一种表达形式，还是使用上面的假设条件：

                 

其结果为：

 

以上的所有说明针对的都是单个样例的情况，而在实际的使用训练过程中，数据往往是组合成为一个batch来使用，所以对用的神经网络的输出应该是一个m*n的二维矩阵，其中m为batch的个数，n为分类数目，而对应的Label也是一个二维矩阵，还是拿上面的数据，组合成一个batch=2的矩阵：

所以交叉熵的结果应该是一个列向量（根据第一种方法）：

而对于一个batch，最后取平均为0.2。

 

通过tensorflow实现交叉熵，其代码实现如下：

cross_entropy=-tf.reduce_mean(y*tf.log(tf.clip_by_value(y,1e-10,1.0)))

其中y_代表正确的结果，y代表预测结果。其中通过tf.clip_by_value函数可以将一个张量中的数值限制在一个范围内，这样可以避免一些运算的错误（比如log0是无效的）。

 

下面给出 tf.clip_by_value的简单例子

v=tf.constant([[1.0,2.0,3.0],[4.0,5.0,6.0]])
print(tf.clip_by_value(v,2.5,4.5).eval())
#输出[[2.5,2.5,3.][4.,4.5,4.5]]

以上代码可以看出，小于2.5的数被换成了2.5，而大于4.5的数被换成了4.5.这样可以通过 tf.clip_by_value 函数保证正在进行的log运算时，不会出现log0这样的错误或者大于1的概率。

因为交叉熵一般会和softmax回归一起使用，所以tensorflow对这两个功能进行了统一封装，并提供了tf.nn.softmax_cross_entropy_with_logits(labels=y_,logits=y),其中y_代表正确的结果，y代表预测结果。这样可以得到使用了softmax回归之后的交叉熵。

二分类交叉熵

对应的是网络单个节点，这个节点将被sigmoid处理，使用阈值分类为0或者1的问题。此类问题logits和labels必须具有相同的type和shape

例子：

import numpy as np
import tensorflow as tf
 
input_data = tf.Variable(np.random.rand(1, 3), dtype=tf.float32)
# np.random.rand()传入一个shape,返回一个在[0,1)区间符合均匀分布的array
 
output = tf.nn.sigmoid_cross_entropy_with_logits(logits=input_data, labels=[[1.0, 0.0, 0.0]])
with tf.Session() as sess:
    init = tf.global_variables_initializer()
    sess.run(init)
    print(sess.run(output))
    # [[ 0.5583781   1.06925142  1.08170223]]

二、多分类交叉熵

对应的是网络输出多个节点，每一个节点表示1个class的得分，使用softmax最终处理的分类问题

原理介绍

cross_entropy = -tf.reduce_mean(y * tf.log(tf.clip_by_value(y_pre, 1e-10, 1.0))

调用一下：

import tensorflow as tf
  
input_data = tf.Variable([[0.2, 0.1, 0.9], [0.3, 0.4, 0.6]], dtype=tf.float32)
labels=tf.constant([[1,0,0], [0,1,0]], dtype=tf.float32)
 
cross_entropy = -tf.reduce_mean(labels * tf.log(tf.clip_by_value(input_data, 1e-10, 1.0)))
                                 
with tf.Session() as sess:
    init = tf.global_variables_initializer()
    sess.run(init)
    print(sess.run(output))

接口介绍：

 

softmax之后，计算输出层全部节点各自的交叉熵（输出向量而非标量）

1 2 3 4 5 6 7

cross_entropy_mean = tf.reduce_mean(     tf.nn.sparse_softmax_cross_entropy_with_logits(         labels=tf.argmax(labels,1), logits=logits), name='cross_entropy')    cross_entropy_mean = tf.reduce_mean(     tf.nn.softmax_cross_entropy_with_logits(         logits=logits, labels=labels), name='cross_entropy')

tf.nn.softmax_cross_entropy_with_logits()

函数的参数label是稀疏表示的，比如表示一个3分类的一个样本的标签，稀疏表示的形式为[0,0,1]这个表示这个样本为第3个分类，而非稀疏表示就表示为2，同理[0,1,0]就表示样本属于第2个分类，而其非稀疏表示为1。

1 2 3 4 5 6 7 8 9

import tensorflow as tf    input_data = tf.Variable([[0.2, 0.1, 0.9], [0.3, 0.4, 0.6]], dtype=tf.float32) output = tf.nn.softmax_cross_entropy_with_logits(logits=input_data, labels=[[1,0,0],                                                                             [0,1,0]]) with tf.Session() as sess:     init = tf.global_variables_initializer()     sess.run(init)     print(sess.run(output))

tf.nn.sparse_softmax_cross_entropy_with_logits()

此函数大致与tf.nn.softmax_cross_entropy_with_logits的计算方式相同,
适用于每个类别相互独立且排斥的情况，一幅图只能属于一类，而不能同时包含一条狗和一只大象

但是在对于labels的处理上有不同之处,labels从shape来说此函数要求shape为[batch_size],
labels[i]是[0,num_classes)的一个索引, type为int32或int64,即labels限定了是一个一阶tensor,
并且取值范围只能在分类数之内,表示一个对象只能属于一个类别

1 2 3 4 5 6 7 8 9

import tensorflow as tf   input_data = tf.Variable([[0.2, 0.1, 0.9], [0.3, 0.4, 0.6]], dtype=tf.float32) output = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=input_data, labels=[0, 2]) with tf.Session() as sess:     init = tf.global_variables_initializer()     sess.run(init)     print(sess.run(output)) # [ 1.36573195  0.93983102]

比tf.nn.softmax_cross_entropy_with_logits多了一步将labels稀疏化的操作。因为深度学习中，图片一般是用非稀疏的标签的，所以tf.nn.sparse_softmax_cross_entropy_with_logits()的频率比tf.nn.softmax_cross_entropy_with_logits高。

不过两者输出尺寸等于输入shape去掉最后一维（上面输入[2*3]，输出[2]），所以均常和tf.reduce_mean()连用。