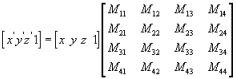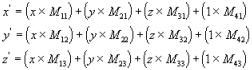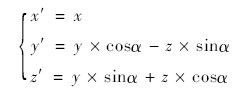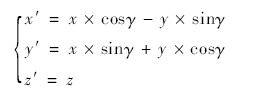Unity3d-旋转Quaternion、Matrix4x4、 Euler

矩阵：Matrix4x4

namespace UnityEngine
{
	public struct Matrix4x4
	{
		public float m00;
		public float m10;
		public float m20;
		public float m30;
		public float m01;
		public float m11;
		public float m21;
		public float m31;
		public float m02;
		public float m12;
		public float m22;
		public float m32;
		public float m03;
		public float m13;
		public float m23;
		public float m33;
      }
}

变换后点的（X’,Y’,Z’）= （x,y,z） *   （ 4*4矩阵）

‍scale：模型的大小变化，在透视投影中用来产生场景深度效果

public static Matrix4x4 Scale(Vector3 v)
{
	return new Matrix4x4
	{
		m00 = v.x,
		m01 = 0f,
		m02 = 0f,
		m03 = 0f,
		m10 = 0f,
		m11 = v.y,
		m12 = 0f,
		m13 = 0f,
		m20 = 0f,
		m21 = 0f,
		m22 = v.z,
		m23 = 0f,
		m30 = 0f,
		m31 = 0f,
		m32 = 0f,
		m33 = 1f
	};
}

translate：物体沿着三个坐标轴的任意一个到另一个位置的移动

rotate：顶点的每个坐标值乘上θ角（物体旋转的角度）的sin或cos值就得到了旋转后的坐标

当点P（x，y，z）绕X轴旋转α度时，点P的x坐标值不变，其旋转前后的坐标关系为：

当点P（x，y，z）绕Y轴旋转β度时，点P的y坐标值不变，其旋转前后的坐标关系为：

当点P（x，y，z）绕Z轴旋转γ度时，点P的z坐标值不变，其旋转前后的坐标关系为：

得出的变换矩阵如下

在unity中Matrix4x4没有单独实现translate和rotate的方法，统一使用SetTRS方法来完成

参见另一篇文章：平移、旋转和缩放矩阵

四元数:Quaternion = (xi + yj + zk + w ) = (x,y,z,w).

四元数是最简单的超复数。 复数是由实数加上元素 i 组成，其中i^2 = -1。 相似地，四元数都是由实数加上三个元素 i、j、k 组成，而且它们有如下的关系： i^2 = j^2 = k^2 = -1 , 每个四元数都是 1、i、j 和 k 的线性组合，即是四元数一般可表示为w + xi + yj + zk，其中x、y、z 、w是实数

namespace UnityEngine
{
	public struct Quaternion
	{
		public float x;
		public float y;
		public float z;
		public float w;
        }
}

四元数中的方向由三个旋转轴（x、y、z）和一个旋转角 (w) 确定
q = cos(A/2)+sin(A/2)*(x*i+y*j+z*k)

Q.w = cos (angle / 2)

Q.x = axis.x * sin (angle / 2)

Q.y = axis.y * sin (angle / 2)

Q.z = axis.z * sin (angle / 2)
四元数可提供平滑差值，没有Euler旋转的万向锁。

四元数到矩阵

public void SetTRS(Vector3 pos, Quaternion q, Vector3 s)

Quaternion q = Quaternion.LookRotation(new Vector3(0,0.5,1));
Matrix4x4 rot = new Matrix4x4();
rot.SetTRS(new Vector3(0,0,0),q,new Vector3(1,1,1));

矩阵到四元数

public void SetLookRotation(Vector3 view, [DefaultValue("Vector3.up")] Vector3 up)

Matrix4x4 rot = new Matrix4x4();
rot.SetTRS(new Vector3(0,0,0),q,new Vector3(1,1,1));
		
Vector4 vy = rot.GetColumn(1);
Vector4 vz = rot.GetColumn(2);
		
Quaternion newQ = Quaternion.LookRotation(new Vector3(vz.x,vz.y,vz.z),new Vector3(vy.x,vy.y,vy.z));
//newQ==q

这个函数建立一个旋转使z轴朝向view y轴朝向up

var obj1: Transform;

var obj2: Transform;

var q:Quaternion;

q.SetLookRotation(obj1.position, obj2.position);

transform.rotation=q;

然后大家拖动obj1和obj2就可以看到物体永远保持z轴朝向obj1， 并且以obj2的位置来保持y轴的倾斜度。

欧拉角：Euler

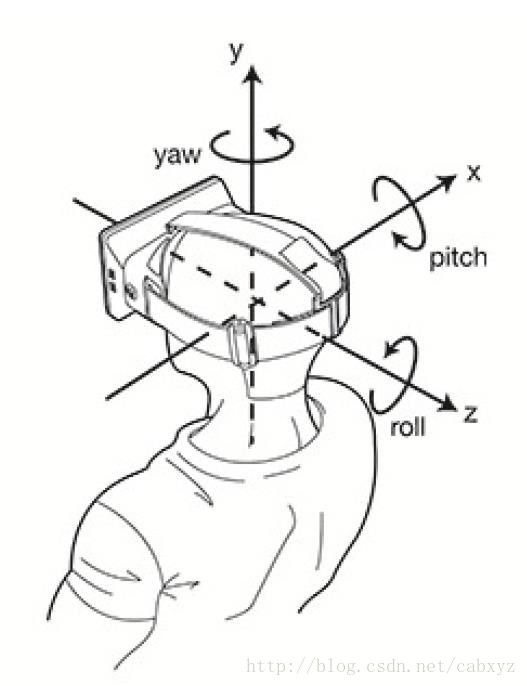
欧拉旋转，我们最常用的旋转方法应该是使用yaw, roll和pitch。

yaw是在XZ轴平面上围绕Y轴左右旋转，当开车时使用的是yaw。

pitch在YZ轴平面上围绕X轴上下旋转，喷气机飞行或爬坡时用pitch向上或向下。

roll是在XY轴平面上绕Z轴倾斜旋转，

从字面意思上说，当你驾驶汽车高速急转弯时，你的汽车会出现roll运动，表现一个方向就可以通过三个欧拉角 (α,β,γ) 来定义。

游戏物体的属性视图中调整的角度就是欧拉角

Quaternion q3 = new Quaternion();
q3.eulerAngles = new Vector3(10, 30, 20);
Quaternion qx3 = Quaternion.AngleAxis(10,Vector3.right);		
Quaternion qy3 = Quaternion.AngleAxis(30,Vector3.up);//绕y轴旋转30度
Quaternion qz3 = Quaternion.AngleAxis(20,Vector3.forward);
		
Quaternion qxyz3 = qz3*qy3*qx3;

上面的代码可以得到q3和qxyz3值一样。从这里可以看出unity中旋转顺序也是按先绕x轴旋转，然后y，最后z。unity中对向量应用旋转量使用的是向量右乘，即如下：

Vector3 newV = qxyz3*v=qz3*qy3*qx3*v;

// A rotation 30 degrees around the y-axis
//绕y轴旋转30度

var rotation = Quaternion.Euler(0, 30, 0);
//返回一个旋转角度，绕z轴旋转z度，绕x轴旋转x度，绕y轴旋转y度（像这样的顺序）。

欧拉角eulerAngles在Unity3D是一个Vector3类的变量，官方约定俗成的层级关系是ZXY，即最里层是Z轴先旋转，中间层是X轴，最外层是Y轴。
unity中的欧拉角有两种方式可以解释:
1,当认为顺序是yxz时（其实就是heading - pitch - bank），是传统的欧拉角变换，也就是以物体自己的坐标系为轴的。
2,当认为顺序是zxy时（roll - pitch - yaw），也是官方文档的顺序时，是以惯性坐标系为轴的。后者比较直观一些，但其实两者的实际效果是一样的，只是理解不一样。

无论以何种方式旋转三个轴，都会有出现万向锁的情况，万向锁主要在动画里面旋转时出现我们不希望见到的旋转路径，所以官方以ZXY顺序来旋转的时候可以最大程度上避免普通情况下会出现的万向锁。

对比：

各方法比较	Matrix4x4	Euler	Quaternion
在坐标系间(物体和惯性)旋转点	能	不能(必须转换到 矩阵)	不能(必须转换到矩阵)
连接或增量旋转	能能,但经常比四元数慢,小心矩阵蠕变的情况	不能	能,比矩阵快
插值	基本上不能	能,但可能遭遇万 向锁或其他问题	Slerp提供了平滑插值
易用程度	难	易	难
在内存或文件中存储	9个数	3个数	4个数
对给定方位的表达方式是否唯一	是	不是,对同一方位 有无数多种方法	不是,有两种方法
可能导致非法	矩阵蠕变	任意三个数都能构成合法的欧拉角	可能会出现误差积累,从而产生非法的四元数