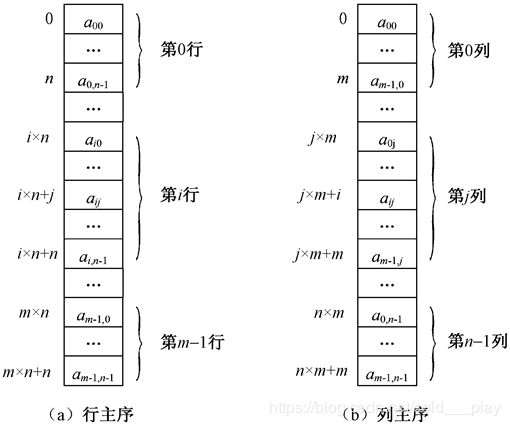
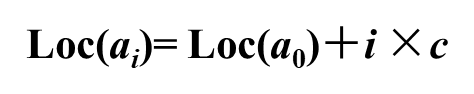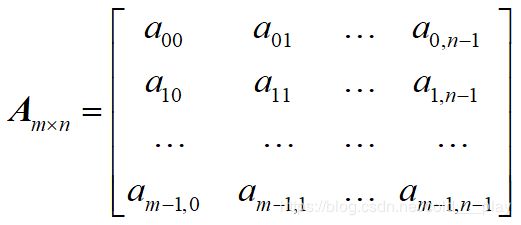数据结构--数组、使用数组表示矩阵
数组
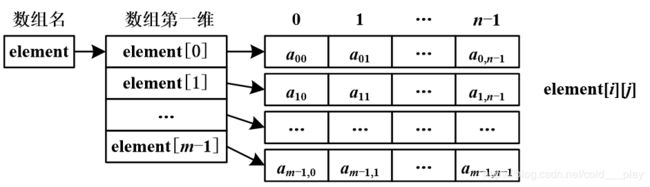
使用数组表示矩阵
package pers.zhang.array;
/**
* @author zhang
* @date 2020/1/19 - 10:36
*
* 矩阵接口
*/
public interface MMatrix {
//返回矩阵第i行第j列元素值
int get(int i, int j);
//设置矩阵第i行第j列元素值
void set(int i, int j, int value);
//矩阵相加,this+=mat,各对应元素相加;改变this矩阵
void add(MMatrix mat);
//返回this与mat相加后的矩阵,不改变this矩阵
MMatrix plus(MMatrix mat);
//返回当前矩阵的转置矩阵
MMatrix transpose();
boolean equals(Object obj);
}
实现:
package pers.zhang.array;
/**
* @author zhang
* @date 2020/1/19 - 10:42
*
* 矩阵类
*/
public class Matrix {
//存储矩阵元素的二维数组
private int element[][];
//构造m*n零矩阵
public Matrix(int m, int n){
this.element = new int[m][n];//数组元素初值为0
}
//构造n*n矩阵
public Matrix(int n){
this(n, n);
}
//构造m*n矩阵,由mat提供元素
public Matrix(int m, int n, int mat[][]){
this(m, n);
for(int i = 0; i < mat.length && i < m; i++)
for(int j = 0; j < mat[i].length && j < n; j++)
this.element[i][j] = mat[i][j];
}
//深拷贝构造
public Matrix(Matrix mat){
this(mat.element.length, mat.element[0].length, mat.element);
}
//返回矩阵第i行第j列元素值,O(1)
public int get(int i, int j){
return this.element[i][j];//若i、j下标越界,Java将抛出数组下标越界异常ArrayIndexOutOfBoundsException
}
//设置矩阵第i行第j列的元素
public void set(int i, int j, int value){
this.element[i][j] = value;
}
//返回矩阵所有元素的描述字符串,行主序遍历
public String toString(){
String str = " 矩阵" + this.getClass().getName() + "(" + this.element.length+"×"+this.element[0].length+"):\n";
for (int i = 0; i < this.element.length; i++){
for (int j = 0; j < this.element[i].length; j++)
str += String.format("%4d", this.element[i][j]);
str += "\n";
}
return str;
}
//当前矩阵与mat矩阵相加,this += mat,各对应元素相加;改变当前矩阵
public void add(Matrix mat){
if(this.element.length != mat.element.length || this.element[0].length != mat.element[0].length)
throw new IllegalArgumentException("两个矩阵阶数不同,不能相加");
for(int i = 0; i < this.element.length; i++)
for(int j = 0; j < this.element[i].length; j++)
this.element[i][j] += mat.element[i][j];
}
//返回当前矩阵与mat相加后的矩阵,不改变当前矩阵,=this+mat,各对应元素相加
public Matrix plus(Matrix mat){
Matrix matc = new Matrix(this); //深拷贝
matc.add(mat);
return matc; //返回对象引用
}
//比较两个同阶矩阵是否相等
public boolean equals(Object obj){
if (this == obj)
return true;
if (!(obj instanceof Matrix))
return false;
Matrix mat = (Matrix)obj;
if (this.element.length != mat.element.length || this.element[0].length != mat.element[0].length)
return false;
for (int i = 0; i < this.element.length; i++)
for (int j = 0; j < this.element[i].length; j++)
if (this.element[i][j]!=mat.element[i][j]) //比较对应元素是否相等
return false;
return true;
}
//返回当前矩阵的转置矩阵
public Matrix transpose(){
Matrix trans = new Matrix(this.element[0].length, this.element.length);//构造零矩阵
for (int i = 0; i < this.element.length; i++)
for (int j = 0; j < this.element[i].length; j++)
trans.element[j][i]=this.element[i][j];
return trans; //返回对象引用
}
//判断当前矩阵是否为上三角矩阵
public boolean isUpTriangular(){
if(this.element.length != this.element[0].length)
return false;
for(int i = 0; i < this.element.length; i++)
for(int j = 0; j < i; j++)
if(this.element[i][j] != 0)//下三角元素应为0
return false;
}
//判断当前矩阵是否为下三角矩阵
public boolean isDownTriangular(){
if(this.element.length != this.element[0].length)
return false;
for (int i = 0; i < this.element.length; i++)
for (int j = i+1; j < this.element.length; j++)
if (this.element[i][j] != 0)//上三角元素应为0
return false;
return true;
}
//判断当前矩阵是否为对称矩阵
public boolean isSymmetric(){
if (this.element.length != this.element[0].length)
return false;
for (int i = 0; i < this.element.length; i++)
for (int j = 0; j < this.element[i].length; j++)
if (this.element[i][j] != this.element[j][i])
return false;
return true;
}
}
测试:
package pers.zhang.array;
/**
* @author zhang
* @date 2020/1/19 - 13:21
*/
public class Matrix_ex {
public static void main(String args[])
{
int m1[][]={{1,2,3},{4,5,6,7,8},{9,10,11}};
Matrix mata=new Matrix(3,4,m1); //矩阵对象,初值不足时自动补0,忽略多余元素
System.out.print("A"+mata.toString());
Matrix matb=new Matrix(3,4); //构造空矩阵对象
matb.set(0,0,1);
matb.set(1,1,1);
matb.set(2,2,1);
System.out.print("B"+matb.toString());
Matrix matc = mata.plus(matb);
System.out.print("C=A+B"+matc.toString());
mata.add(matb);
System.out.print("A+=B"+mata.toString());
//习题5
System.out.println("\n//习题5");
System.out.println("C.equals(A)?"+matc.equals(mata));
System.out.print("A的转置矩阵"+mata.transpose().toString());
System.out.print("B的转置矩阵"+matb.transpose().toString()+"\n");
System.out.println("A是上三角矩阵?"+mata.isUpTriangular());
int m2[][]={{1,2,3,4},{0,5,6,7},{0,0,8,9}};
Matrix mate=new Matrix(4,4,m2); //初值不足时自动补0
System.out.print("E"+mate.toString());
System.out.println("E是上三角矩阵?"+mate.isUpTriangular()+"\n");
System.out.println("A是下三角矩阵?"+mata.isDownTriangular());
int m3[][]={{1},{2,3},{0,4},{5,6,7}}; //初值不足时自动补0
Matrix matf=new Matrix(4,4,m3);
System.out.print("F"+matf.toString());
System.out.println("F是下三角矩阵?"+matf.isDownTriangular()+"\n");
System.out.println("A是对称矩阵?"+mata.isSymmetric());
int m4[][]={{1,2,3,4},{2},{3},{4}};
Matrix matg=new Matrix(4,4,m4);
System.out.print("G"+matg.toString());
System.out.println("G是对称矩阵?"+matg.isSymmetric());
}
}
/*
程序运行结果如下:
A 矩阵Matrix(3×4):
1 2 3 0
4 5 6 7
9 10 11 0
B 矩阵Matrix(3×4):
1 0 0 0
0 1 0 0
0 0 1 0
C=A+B 矩阵Matrix(3×4):
2 2 3 0
4 6 6 7
9 10 12 0
A+=B 矩阵Matrix(3×4):
2 2 3 0
4 6 6 7
9 10 12 0
//习题5
C.equals(A)?true
A的转置矩阵 矩阵Matrix(4×3):
2 4 9
2 6 10
3 6 12
0 7 0
B的转置矩阵 矩阵Matrix(4×3):
1 0 0
0 1 0
0 0 1
0 0 0
A是上三角矩阵?false
E 矩阵Matrix(4×4):
1 2 3 4
0 5 6 7
0 0 8 9
0 0 0 0
E是上三角矩阵?true
A是下三角矩阵?false
F 矩阵Matrix(4×4):
1 0 0 0
2 3 0 0
0 4 0 0
5 6 7 0
F是下三角矩阵?true
A是对称矩阵?false
G 矩阵Matrix(4×4):
1 2 3 4
2 0 0 0
3 0 0 0
4 0 0 0
G是对称矩阵?true
*/