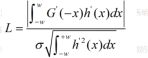边缘检测

4. 边缘检测：Edge Detection 我们要找水平的边缘：需要注意的是，这里矩阵的元素和是0，所以滤波后的图像会很暗，只有边缘的地方是有亮度的。边缘是图像中灰度发生急剧变化的区域边界。图像灰度的变化情况可以用图像灰度分布的梯度来表示，数字图像中求导是利用差分近似微分来进行的，实际上常用空域微分算子通过卷积来完成。

一般图像边缘检测方法主要有如下四个步骤：

（1）图像滤波：传统边缘检测算法主要是基于图像强度的一阶和二阶导数，但导数的计算对噪声很敏感，因此必须使用滤波器来改善与噪声有关的边缘检测器的性能。需要指出的是，大多数滤波器在降低噪声的同时也造成了了边缘强度的损失，因此，在增强边缘和降低噪声之间需要一个折衷的选择。

（2）图像增强：增强边缘的基础是确定图像各点邻域强度的变化值。增强算法可以将邻域(或局部)强度值有显著变化的点突显出来。边缘增强一般是通过计算梯度的幅值来完成的。

（3）图像检测：在图像中有许多点的梯度幅值比较大，而这些点在特定的应用领域中并不都是边缘，所以应该用某种方法来确定哪些点是边缘点。最简单的边缘检测判断依据是梯度幅值。

（4）图像定位：如果某一应用场合要求确定边缘位置，则边缘的位置可在子像素分辨率上来估计，边缘的方位也可以被估计出来。近20多年来提出了许多边缘检测算子。

一阶导数算子

1）Roberts算子：是一种斜向偏差分的梯度计算方法，梯度的大小代表边缘的强度，梯度的方向与边缘的走向垂直。Roberts操作实际上是求旋转45度两个方向上微分值的和。定位精度高，在水平和垂直方向的效果好，但对噪声敏感。两个卷积核Gx、Gy分别为

                                            

采用1范数衡量梯度的幅度为=。如果梯度G大于某一阀值 则认为该点(x,y)为边缘点。

2)Sobel算子：是一组方向算子，从不同的方向检测边缘。Sobel算子不是简单的求平均再差分，而是加强了中心像素上下左右4个方向像素的权值，运算结果是一副边缘图。Sobel算子通常对灰度渐变和噪声较多的图像处理的比较好。两个卷积核Gx、Gy分别为：

                               

采用范数衡量梯度的幅度为。如果梯度G大于某一阀值 则认为该点(x,y)为边缘点。

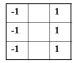
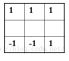
3）Prewitt算子：是一种边缘样板算子，利用像素点上下左右邻点灰度差，在边缘处达到极值检测边缘，对噪声具有平滑的作用。由于边缘点像素的灰度值与其邻域点的灰度值显著不同，在实际应用中通常采用微分算子和模板匹配的方法检测图像的边缘。Prewitt算子不仅能检测边缘点，而且能抑制噪声的影响，因此对灰度和噪声较多的图像处理得比较好。两个卷积核Gx、Gy分别为：

                                   

采用范数衡量梯度的幅度为：。如果梯度G大于某一阀值 则认为该点(x,y)为边缘点。

二阶导数算子也可以检测边缘，利用二阶导数算子检测阶梯状边缘需将检测算子与图像卷积并确定过零点。

1)  Laplacian算子：拉普拉斯算子是一种常用的二阶导数算子。实际中可根据二阶导数算子过零点的性质来确定边缘的位置。对于一个连续函数f(x,y),它在位置(x,y)的拉普拉斯值定义如下：

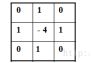
在图像中，计算函数的拉普拉斯值也可借助各种模板实现。这里对模板的基本要求是对应中心像素的系数应是正的，而对应中心像素邻近像素的系数应是负的，且它们的和应该是零。拉普拉斯算子检测方法常常产生双像素边界，而且这个检测方法对图像中的噪声相当敏感，不能检测边缘的方向，所以很少直接使用拉普拉斯算子进行边缘检测。常用的两种模板分别如图所示：

                   

2）LOG算法：

LOG算法步骤如下：1、 取样得到的高斯低通滤波器对输入图像滤波。2、 计算第一步得到图像的拉普拉斯。3、 找到步骤2所得图像的零交叉。

3)  Canny算子：Canny算子把边缘检测问题转换为检测单位函数极大值的问题来考虑。他利用高斯模型，借助图像滤波的概念指出一个好的边缘检测算子应该具有3个指标：1.低失误率，既要少将真的边缘丢弃，也要少将非边缘判为边缘；2.高位置精度，检测出的边缘应在真正的边界上；3.单像素边缘，即对每个边缘有唯一的响应，得到的边界为单像素宽。

考虑到上述三个条件，Canny提出了判定边缘检测算子的3个准则：信噪比准则、定位精度准则和单边缘响应准则。

1. 信噪比准则：信噪比越大，提取的边缘质量越高。信噪比SNR定义为

 

2.  定位精度准则边缘定位的精度L定义如下

其中，G’(x)和h’(x)分别是G(x)和h(x)的导数。L越大表明定位精度越高。

3. 单边缘响应准则：为了保证单边缘只有一个响应。检测算子的脉冲响应导数的零交叉点的平均距离D(f’)应满足

满足上述三个条件的算子称为Canny算子。Canny边缘检测算法的步骤如下:

(1) 用高斯滤波器平滑图像；(2)用一阶偏导的有限差分来计算梯度的幅值和方向；(3)对梯度幅值进行非极大值抑制；（排除非边缘像素，仅仅保留细线条）(4)用双阈值算法进行检测和链接边缘。

Robert：边缘定位精度较高，对于陡峭边缘且噪声低的图像效果较好，但没有进行平滑处理，没有抑制噪声的能力。

sobel和prewitt：进行了平滑处理，对噪声具有一定抑制能力，但容易出现多像素宽度。精度不高，边缘较粗糙。

Laplacian：对噪声较为敏感，使噪声能力成分得到加强，容易丢失部分边缘方向信息，造成一些不连续的检测边缘，抗噪声能力较差。

log：抗噪声能力较强，但会造成一些尖锐的边缘无法检测到。

canny：最优化思想的边缘检测算子，同时采用高斯函数对图像进行平滑处理，但会造成将高频边缘平滑掉，造成边缘丢失，采用双阈值算法检测和连接边缘。