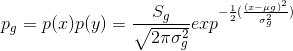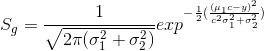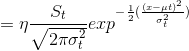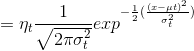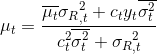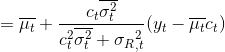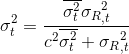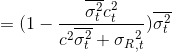- Python OpenCV图像处理:从基础到高级的全方位指南
极客代码
玩转Python开发语言pythonopencv图像处理计算机视觉
目录第一部分:PythonOpenCV图像处理基础1.1OpenCV简介1.2PythonOpenCV安装1.3实战案例:图像显示与保存1.4注意事项第二部分:PythonOpenCV图像处理高级技巧2.1图像变换2.2图像增强2.3图像复原第三部分:PythonOpenCV图像处理实战项目3.1图像滤波3.2图像分割3.3图像特征提取第四部分:PythonOpenCV图像处理注意事项与优化策略4
- Open3D 实现CSF布料模拟算法
今夕是何年,
单目+双目Open3d计算机视觉
目录一、算法原理二,详细过程三,环境安装四,代码实现五,结果展示6,在cloudcompare中的实现一、算法原理1、流程概述1)利用点云·滤波算法或者点云处理软件滤除异常点;2)将激光雷达点云倒置;3)设置模拟布料,设置布料网格分辨率GR,确定模拟粒子数。布料的位置设置在点云最高点以上;4)将布料模拟点和雷达点投影到水平面,为每个布料模拟点找到最相邻的激光点的高度值,将高度值设置为IHV;5)布
- 2023-08-20
Leslie91
活在当下和活在未来并不对立,就像确认攀登一坐高山,设定自己的目标和计划,一路前行。适当停留领略周边风景稍做调整休息,继续登高。活在未来的思维逻辑让我有时间紧迫感,训练主动前瞻行思维和坚定执行力;活在当下是让我体验世界的一切美好和不经意收获的感动。用贝叶斯定律从新修正自己的观点:用30%时间体验当下人世间酸甜苦辣,因为我活着;用70%时间去活在未来,因为前方有更广阔的视野和更多的收获,每时每刻都要按
- 概率图模型(PGM)综述
医学影像处理
概率图模型概率图模型综述
RefLink:http://www.sigvc.org/bbs/thread-728-1-1.htmlGraphicalModel的基本类型基本的GraphicalModel可以大致分为两个类别:贝叶斯网络(BayesianNetwork)和马尔可夫随机场(MarkovRandomField)。它们的主要区别在于采用不同类型的图来表达变量之间的关系:贝叶斯网络采用有向无环图(DirectedAc
- 曲线的平滑平滑处理
zq4132
c++qtc数据算法
最近在写一些数据处理的程序。经常需要对数据进行平滑处理。直接用FIR滤波器或IIR滤波器都有一个启动问题,滤波完成后总要对数据掐头去尾。因此去找了些简单的数据平滑处理的方法。在一本老版本的《数学手册》中找到了几个基于最小二乘法的数据平滑算法。将其写成了C代码,测试了一下,效果还可以。这里简单的记录一下,算是给自己做个笔记。算法的原理很简单,以五点三次平滑为例。取相邻的5个数据点,可以拟合出一条3次
- 潜在狄利克雷分配(Latent Dirichlet Allocation,LDA)—无监督学习方法、概率模型、生成模型、线性模型、非参数化模型、贝叶斯学习、批量学习
剑海风云
ArtificialIntelligence人工智能机器学习潜在狄利克雷分配LDA
定义输入:单词集合W={ω1,⋯ ,ωv,⋯ ,ωV},其中ωv是第v个单词,v=1,2,⋯ ,V,V是单词第个数。单词集合W=\{\omega_1,\cdots,\omega_v,\cdots,\omega_V\},其中\omega_v是第v个单词,v=1,2,\cdots,V,V是单词第个数。单词集合W={ω1,⋯,ωv,⋯,ωV},其中ωv是第v个单词,v=1,2,⋯,V,V是单词第个数。文
- OpenCV高阶操作
富士达幸运星
opencv人工智能计算机视觉
在图像处理与计算机视觉领域,OpenCV(OpenSourceComputerVisionLibrary)无疑是最为强大且广泛使用的工具之一。从基础的图像读取、1.图片的上下,采样下采样(Downsampling)下采样通常用于减小图像的尺寸,从而减少图像中的像素数。这个过程可以通过多种方法实现,但最常见的是通过图像金字塔中的pyrDown函数(在OpenCV中)或其他类似的滤波器(如平均池化、最
- c语言用一维数组做中值滤波,快速中值滤波及c语言实现
快手镜相
c语言用一维数组做中值滤波
快速中值滤波及c语言实现学生姓名:刘勇学号:6100410218专业班级:数媒101【摘要】本文讨论了用c语言在微机上实现中值滤波及快速算法,在程序设计的过程中充分考虑到程序运行的时间复杂度和空间复杂度的问题.解决了由于图像太大而内存不够的问题,运用对程序运行时的方法,得出在PENTIUM-S100MHz上中值滤渡的一般算法运行4.23秒.而快速算法运行258秒。【关键词】c语言;中值滤波;快速算
- 【机器学习】朴素贝叶斯
可口的冰可乐
机器学习机器学习概率论
3.朴素贝叶斯素贝叶斯算法(NaiveBayes)是一种基于贝叶斯定理的简单而有效的分类算法。其“朴素”之处在于假设各特征之间相互独立,即在给定类别的条件下,各个特征是独立的。尽管这一假设在实际中不一定成立,合理的平滑技术和数据预处理仍能使其在许多任务中表现良好。优点:速度快:由于朴素贝叶斯仅需计算简单的概率,训练和预测的速度非常快。适用于高维数据:即使在特征数量多的情况下,朴素贝叶斯仍然表现良好
- MATLAB车牌定位和识别系统
清风明月来几时
图像算法处理matlab开发语言
有很多方法可以实现MATLAB车牌的定位和识别系统。以下是一种可能的实现步骤:车牌定位:使用图像处理技术(如边缘检测、区域生长或颜色分割)来检测图像中的车牌区域。使用形态学操作来排除不符合车牌形状的区域。对车牌区域进行裁剪或调整大小,以便后续的识别。车牌识别:将车牌图像转换为灰度图像。使用图像处理技术(如二值化、滤波或增强)来减少噪音并突出字符。使用字符分割算法将车牌中的字符分开。使用特征提取方法
- 机器学习实战笔记5——线性判别分析
绍少阿
机器学习笔记可视化机器学习python人工智能
任务安排1、机器学习导论8、核方法2、KNN及其实现9、稀疏表示3、K-means聚类10、高斯混合模型4、主成分分析11、嵌入学习5、线性判别分析12、强化学习6、贝叶斯方法13、PageRank7、逻辑回归14、深度学习线性判别分析(LDA)Ⅰ核心思想对于同样一件事,站在不同的角度,我们往往会有不同的看法,而降维思想,亦是如此。同上节课一样,我们还是学习降维的算法,只是提供了一种新的角度,由上
- 【机器学习】近似推断的基本概念以及变分贝叶斯的基本概念
Lossya
机器学习人工智能python贝叶斯网络变分贝叶斯近似推断
引言近似推断是处理大规模或复杂概率图模型时常用的一种方法,特别是在精确推断变得不可行或不实际的情况下文章目录引言一、近似推断1.1常见的近似推断方法1.1.1采样方法(SamplingMethods)1.1.1.1马尔可夫链蒙特卡洛(MCMC)1.1.1.2重要性采样(ImportanceSampling)1.1.1.3蒙特卡洛模拟(MonteCarloSimulation)1.1.2变分推断(V
- 计算机视觉之旅-进阶-图像滤波处理
撸码猿
计算机视觉图像处理人工智能
1.基本概念1.1.数字图像图像处理的对象是数字图像,它是由像素点阵列表示的图像。需要了解像素、图像分辨率、灰度级、RBG等图像表示方法。用numpy数组表示,每个元素为像素值。例如RGB图像 importnumpyasnp img=np.array([[[255,0,0],[0,255,0]],[[0,0,255],[255,255,255]]]) 1.2.采样和量化数字图像是通过采样和量化得到
- 数字图像处理(一系列对图像进行处理、分析和改进的技术)
编程日记✧
智能医疗计算机视觉图像处理人工智能
数字图像处理是指对图像进行一系列的数学和算法处理,以增强、分析或理解图像的内容。这些处理包括从基础的像素操作到复杂的高维变换和机器学习模型。1.图像降噪在图像获取和传输过程中,往往会引入噪声。降噪技术用于减少这些噪声,同时尽量保持图像的细节。常见方法有:均值滤波:将像素邻域内的像素值取平均值,从而平滑图像。这种方法简单但可能会模糊边缘。高斯滤波:使用高斯函数为权重对像素进行加权平均,可以更好地平滑
- 9. 卷积神经网络工程实践
路小漫
小姐姐归来,带着蜜汁微笑,啦啦啦~这次讲的应该是一些成功的神经网络架构,毕竟我们不能总重复造轮子,借鉴很重要AlexNet结构AlexNet的架构如图,有5个卷积层问题1输入是:227×227×3的图像第一层(卷积层1):96个大小为11×11的滤波器,步长为4问题:卷积层的输出是?*答案:55×55×96问题2问题:这一层的超参数的个数是多少?答案:(11×11×3)×96=35k问题3输入:2
- 基于深度学习的信号滤波:创新技术与应用挑战
逼子歌
深度学习神经网络信号滤波图像去噪卷积神经网络长短期记忆网络
一、引言1.1研究背景随着科技的不断发展,信号处理领域面临着越来越复杂的挑战。在众多信号处理技术中,基于深度学习的信号滤波技术逐渐崭露头角,成为研究的热点。基于深度学习的信号滤波在信号处理领域具有至关重要的地位。如今,我们生活在一个数据爆炸的时代,各种信号源不断产生大量的复杂数据。例如,在通信领域,信号常常受到噪声干扰,传统的滤波方法在处理复杂、非线性信号时可能效果不佳。而深度学习技术具有自动特征
- [草稿]关于冲击响应,低通滤波器和高通滤波器,响应曲线和功能的直观理解
Deno_V
信号处理自动化
失眠时突然回忆起原来的学的东西,产生了几个疑问:为什么可以用冲击函数的组合去表示信号?这个信号又是怎么变成冲击函数信号的组合的?我们都知道H(s)=1/(s+1)是低通滤波器,我们也知道他冲击响应的时域信号的形状,那么这个随时间衰减的形状为什么就会是低通的呢?我们都知道H(s)=s/(s+1)是高通滤波器,为什么和低通比起来他仅仅只是分子多了个s,这个s的在物理世界的含义是什么?躺在床上想着想着睡
- 【统计学习方法读书笔记】(四)朴素贝叶斯法
Y.G Bingo
统计学习方法人工智能统计学习概率概率论
终于到了贝叶斯估计这章了,贝叶斯估计在我心中一直是很重要的地位,不过发现书中只用了不到10页介绍这一章,深度内容后,发现贝叶斯估计的基础公式确实不多,但是由于正态分布在生活中的普遍性,贝叶斯估计才应用的非常多吧!默认输入变量用XXX表示,输出变量用YYY表示概率公式描述:P(X=x)P(X=x)P(X=x):表示当X=xX=xX=x时的概率P(X=x∣Y=ck)P(X=x|Y=c_k)P(X=x∣
- 汽车智能驾驶算法汇总
芊言芊语
汽车算法
汽车智能驾驶算法是自动驾驶技术的核心,它们集成了多个学科的知识,包括计算机视觉、机器学习、控制理论、路径规划等。以下是对汽车智能驾驶算法的一个详细汇总,内容分为几个关键部分进行阐述。一、计算机视觉算法计算机视觉是智能驾驶算法中用于识别和理解环境的关键技术。它主要包括图像处理、特征提取和对象识别等步骤。图像处理:通过摄像头等设备获取车辆前方的图像,然后进行预处理,如灰度化、二值化、滤波等操作,以提高
- 【电子电力】带LCL滤波器的滞后电流控制单相并网光伏逆变器系统
梦想科研社
matlab
摘要带LCL滤波器的滞后电流控制单相并网光伏逆变器系统是一种用于将太阳能光伏发电并入电网的高效电力转换系统。滞后电流控制方式通过快速响应和高精度的电流跟踪,确保了电力的高质量输出,而LCL滤波器则有效减少了逆变器产生的谐波干扰,提高了并网电流的质量。本研究探讨了该系统的工作原理、实验结果及其在实际应用中的表现。理论单相并网光伏逆变器系统的主要功能是将光伏组件产生的直流电转换为交流电,并以高质量的电
- 【PSINS】SINS与航位推算的EKF例程讲解|三维轨迹
MATLAB卡尔曼
基于PSINS工具箱的程序设计androidmatlabpsins
文章目录SINS与航位推算例程构造滤波前滤波主体滤波后处理运行结果源代码SINS与航位推算SINS是捷联惯导,略。航位推算:本文讲解的程序是PSINS工具箱(相关文章:PSINS初学指导,https://blog.csdn.net/callmeup/article/details/136459824)的一个函数,在此基础上进行优化。如果要运行,需要先安装工具箱。例程构造滤波前下图蓝色轨迹:滤波主体
- 人脸识别技术框架
weixin_30314813
人工智能
1、人脸检测(确定人脸的位置)。2、人脸关键点(确定眼睛,嘴角等特征位置)。3、人脸几何校正(把人脸通过缩放、旋转、拉伸等图像变化到一个比较标准的大小位置)。4、人脸光学校正(滤波,去除一些对光照敏感的面部特征)。5、人脸特征提取(包括LBP,HOG,Gabor等)。6、人脸识别转载于:https://www.cnblogs.com/lanye/p/3620621.html
- 大厂嵌入式数字信号处理器(DSP)面试题及参考答案
大模型大数据攻城狮
单片机嵌入式面试模数装换器离散信号信号处理滤波器嵌入式芯片
什么是模拟信号处理和数字信号处理(DSP)在嵌入式系统中的应用?模拟信号处理是对连续变化的模拟信号进行操作和处理。在嵌入式系统中,模拟信号处理的应用包括传感器信号的调理,例如温度传感器、压力传感器等输出的模拟信号通常比较微弱且可能受到噪声干扰,需要通过放大器进行放大,通过滤波器去除噪声等操作,使其能够被后续的模数转换电路准确地转换为数字信号。数字信号处理(DSP)则是对离散的数字信号进行各种算法处
- fpga图像处理实战-边缘检测 (Roberts算子)
梦梦梦梦子~
OV5640+图像处理图像处理计算机视觉人工智能
Roberts算子Roberts算子是一种用于边缘检测的算子,主要用于图像处理中检测图像的边缘。它是最早的边缘检测算法之一,以其计算简单、速度快而著称。Roberts算子通过计算图像像素在对角方向的梯度来检测边缘,从而突出图像中灰度变化最剧烈的部分。原理Roberts算子通过对图像应用两个2x2的卷积核(也称为掩模或滤波器)来计算图像在水平和垂直方向上的梯度。假设原始图像的像素值为I(x,y),则
- 1-19 平滑处理——双边滤波 opencv树莓派4B 入门系列笔记
Sisphusssss
树莓派opencv笔记人工智能计算机视觉算法
目录一、提前准备二、代码详解cv2.bilateralFilter函数用于对图像进行双边滤波。双边滤波是一种保持边缘的平滑技术,常用于图像去噪声和增强图像的细节。函数的四个参数如下:三、运行现象四、完整工程贴出一、提前准备1、树莓派4B及64位系统2、提前安装opencv库以及numpy库3、保存一张图片二、代码详解importcv2#读取图像img=cv2.imread('/home/raspb
- 【机器学习】朴素贝叶斯方法的概率图表示以及贝叶斯统计中的共轭先验方法
Lossya
机器学习概率论人工智能朴素贝叶斯共轭先验
引言朴素贝叶斯方法是一种基于贝叶斯定理的简单概率模型,它假设特征之间相互独立。文章目录引言一、朴素贝叶斯方法的概率图表示1.1节点表示1.2边表示1.3无其他连接1.4总结二、朴素贝叶斯的应用场景2.1文本分类2.2推荐系统2.3医疗诊断2.4欺诈检测2.5情感分析2.6邮件过滤2.7信息检索2.8生物信息学三、朴素贝叶斯的优点四、朴素贝叶斯的局限性4.1特征独立性假设4.2敏感于输入数据的表示4
- 【机器学习】朴素贝叶斯网络的基本概念以及朴素贝叶斯网络在python中的实例
Lossya
机器学习python人工智能算法朴素贝叶斯
引言文章目录引言一、朴素贝叶斯网络1.1基本概念1.1.1节点1.1.2边(Edges)1.1.3条件独立性1.2特点1.2.1结构简单1.2.2易于理解和实现1.2.3计算效率高1.3应用1.4数学表示1.5局限性二、朴素贝叶斯网络在python中的实例2.1实例背景2.2实现步骤2.3python代码2.4代码解释三、概率推断在医疗领域中的使用3.1概率推断在医疗领域的使用3.2自动化推断的优
- Python(TensorFlow)和Java及C++受激发射损耗导图
亚图跨际
Python交叉知识算法去噪预测算法聚焦荧光团伪影消除算法囊泡动力学自动化多尺度统计物距
要点神经网络监督去噪预测算法聚焦荧光团和检测模拟平台伪影消除算法性能优化方法自动化多尺度囊泡动力学成像生物研究多维分析统计物距粒子概率算法Python和MATLAB图像降噪算法消除噪声的一种方法是将原始图像与表示低通滤波器或平滑操作的掩模进行卷积。例如,高斯掩模包含由高斯函数确定的元素。这种卷积使每个像素的值与其相邻像素的值更加协调。一般来说,平滑滤波器将每个像素设置为其自身及其附近相邻像素的平均
- 01-30
姬汉斯
今天看的是关于文档识别和分类的处理案例。利用多项式贝叶斯公式计算TF-IDF值,以此计算出文档中的词频,文档频率等数据属性,TFIDFVectorizer类用于进行整理,NTLK包进行标注处理,计算文档中各个字符的权重,通过分类器进行分类处理。Sklearn在其中依然有巨大作用,还在熟悉其特性
- 图像去噪技术:自适应均值滤波器(ACmF)
潦草通信狗
均值算法算法人工智能图像处理信息与通信matlab
在图像处理领域,噪声是影响图像质量和视觉感知的主要因素之一。椒盐噪声是一种常见的噪声类型,它随机地将像素值改变为最小值或最大值,严重影响图像的视觉效果。为了解决这一问题,我们开发了一种自适应均值滤波器(ACmF),它能够有效地去除椒盐噪声,同时保留图像的重要细节。一、ACmF算法简介ACmF算法是一种基于局部像素值的自适应去噪方法。它通过分析图像的局部区域,对噪声像素进行智能处理,以恢复图像的原始
- 解线性方程组
qiuwanchi
package gaodai.matrix;
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Test {
public static void main(String[] args) {
Scanner scanner = new Sc
- 在mysql内部存储代码
annan211
性能mysql存储过程触发器
在mysql内部存储代码
在mysql内部存储代码,既有优点也有缺点,而且有人倡导有人反对。
先看优点:
1 她在服务器内部执行,离数据最近,另外在服务器上执行还可以节省带宽和网络延迟。
2 这是一种代码重用。可以方便的统一业务规则,保证某些行为的一致性,所以也可以提供一定的安全性。
3 可以简化代码的维护和版本更新。
4 可以帮助提升安全,比如提供更细
- Android使用Asynchronous Http Client完成登录保存cookie的问题
hotsunshine
android
Asynchronous Http Client是android中非常好的异步请求工具
除了异步之外还有很多封装比如json的处理,cookie的处理
引用
Persistent Cookie Storage with PersistentCookieStore
This library also includes a PersistentCookieStore whi
- java面试题
Array_06
java面试
java面试题
第一,谈谈final, finally, finalize的区别。
final-修饰符(关键字)如果一个类被声明为final,意味着它不能再派生出新的子类,不能作为父类被继承。因此一个类不能既被声明为 abstract的,又被声明为final的。将变量或方法声明为final,可以保证它们在使用中不被改变。被声明为final的变量必须在声明时给定初值,而在以后的引用中只能
- 网站加速
oloz
网站加速
前序:本人菜鸟,此文研究总结来源于互联网上的资料,大牛请勿喷!本人虚心学习,多指教.
1、减小网页体积的大小,尽量采用div+css模式,尽量避免复杂的页面结构,能简约就简约。
2、采用Gzip对网页进行压缩;
GZIP最早由Jean-loup Gailly和Mark Adler创建,用于UNⅨ系统的文件压缩。我们在Linux中经常会用到后缀为.gz
- 正确书写单例模式
随意而生
java 设计模式 单例
单例模式算是设计模式中最容易理解,也是最容易手写代码的模式了吧。但是其中的坑却不少,所以也常作为面试题来考。本文主要对几种单例写法的整理,并分析其优缺点。很多都是一些老生常谈的问题,但如果你不知道如何创建一个线程安全的单例,不知道什么是双检锁,那这篇文章可能会帮助到你。
懒汉式,线程不安全
当被问到要实现一个单例模式时,很多人的第一反应是写出如下的代码,包括教科书上也是这样
- 单例模式
香水浓
java
懒汉 调用getInstance方法时实例化
public class Singleton {
private static Singleton instance;
private Singleton() {}
public static synchronized Singleton getInstance() {
if(null == ins
- 安装Apache问题:系统找不到指定的文件 No installed service named "Apache2"
AdyZhang
apachehttp server
安装Apache问题:系统找不到指定的文件 No installed service named "Apache2"
每次到这一步都很小心防它的端口冲突问题,结果,特意留出来的80端口就是不能用,烦。
解决方法确保几处:
1、停止IIS启动
2、把端口80改成其它 (譬如90,800,,,什么数字都好)
3、防火墙(关掉试试)
在运行处输入 cmd 回车,转到apa
- 如何在android 文件选择器中选择多个图片或者视频?
aijuans
android
我的android app有这样的需求,在进行照片和视频上传的时候,需要一次性的从照片/视频库选择多条进行上传
但是android原生态的sdk中,只能一个一个的进行选择和上传。
我想知道是否有其他的android上传库可以解决这个问题,提供一个多选的功能,可以使checkbox之类的,一次选择多个 处理方法
官方的图片选择器(但是不支持所有版本的androi,只支持API Level
- mysql中查询生日提醒的日期相关的sql
baalwolf
mysql
SELECT sysid,user_name,birthday,listid,userhead_50,CONCAT(YEAR(CURDATE()),DATE_FORMAT(birthday,'-%m-%d')),CURDATE(), dayofyear( CONCAT(YEAR(CURDATE()),DATE_FORMAT(birthday,'-%m-%d')))-dayofyear(
- MongoDB索引文件破坏后导致查询错误的问题
BigBird2012
mongodb
问题描述:
MongoDB在非正常情况下关闭时,可能会导致索引文件破坏,造成数据在更新时没有反映到索引上。
解决方案:
使用脚本,重建MongoDB所有表的索引。
var names = db.getCollectionNames();
for( var i in names ){
var name = names[i];
print(name);
- Javascript Promise
bijian1013
JavaScriptPromise
Parse JavaScript SDK现在提供了支持大多数异步方法的兼容jquery的Promises模式,那么这意味着什么呢,读完下文你就了解了。
一.认识Promises
“Promises”代表着在javascript程序里下一个伟大的范式,但是理解他们为什么如此伟大不是件简
- [Zookeeper学习笔记九]Zookeeper源代码分析之Zookeeper构造过程
bit1129
zookeeper
Zookeeper重载了几个构造函数,其中构造者可以提供参数最多,可定制性最多的构造函数是
public ZooKeeper(String connectString, int sessionTimeout, Watcher watcher, long sessionId, byte[] sessionPasswd, boolea
- 【Java命令三】jstack
bit1129
jstack
jstack是用于获得当前运行的Java程序所有的线程的运行情况(thread dump),不同于jmap用于获得memory dump
[hadoop@hadoop sbin]$ jstack
Usage:
jstack [-l] <pid>
(to connect to running process)
jstack -F
- jboss 5.1启停脚本 动静分离部署
ronin47
以前启动jboss,往各种xml配置文件,现只要运行一句脚本即可。start nohup sh /**/run.sh -c servicename -b ip -g clustername -u broatcast jboss.messaging.ServerPeerID=int -Djboss.service.binding.set=p
- UI之如何打磨设计能力?
brotherlamp
UIui教程ui自学ui资料ui视频
在越来越拥挤的初创企业世界里,视觉设计的重要性往往可以与杀手级用户体验比肩。在许多情况下,尤其对于 Web 初创企业而言,这两者都是不可或缺的。前不久我们在《右脑革命:别学编程了,学艺术吧》中也曾发出过重视设计的呼吁。如何才能提高初创企业的设计能力呢?以下是 9 位创始人的体会。
1.找到自己的方式
如果你是设计师,要想提高技能可以去设计博客和展示好设计的网站如D-lists或
- 三色旗算法
bylijinnan
java算法
import java.util.Arrays;
/**
问题:
假设有一条绳子,上面有红、白、蓝三种颜色的旗子,起初绳子上的旗子颜色并没有顺序,
您希望将之分类,并排列为蓝、白、红的顺序,要如何移动次数才会最少,注意您只能在绳
子上进行这个动作,而且一次只能调换两个旗子。
网上的解法大多类似:
在一条绳子上移动,在程式中也就意味只能使用一个阵列,而不使用其它的阵列来
- 警告:No configuration found for the specified action: \'s
chiangfai
configuration
1.index.jsp页面form标签未指定namespace属性。
<!--index.jsp代码-->
<%@taglib prefix="s" uri="/struts-tags"%>
...
<s:form action="submit" method="post"&g
- redis -- hash_max_zipmap_entries设置过大有问题
chenchao051
redishash
使用redis时为了使用hash追求更高的内存使用率,我们一般都用hash结构,并且有时候会把hash_max_zipmap_entries这个值设置的很大,很多资料也推荐设置到1000,默认设置为了512,但是这里有个坑
#define ZIPMAP_BIGLEN 254
#define ZIPMAP_END 255
/* Return th
- select into outfile access deny问题
daizj
mysqltxt导出数据到文件
本文转自:http://hatemysql.com/2010/06/29/select-into-outfile-access-deny%E9%97%AE%E9%A2%98/
为应用建立了rnd的帐号,专门为他们查询线上数据库用的,当然,只有他们上了生产网络以后才能连上数据库,安全方面我们还是很注意的,呵呵。
授权的语句如下:
grant select on armory.* to rn
- phpexcel导出excel表简单入门示例
dcj3sjt126com
PHPExcelphpexcel
<?php
error_reporting(E_ALL);
ini_set('display_errors', TRUE);
ini_set('display_startup_errors', TRUE);
if (PHP_SAPI == 'cli')
die('This example should only be run from a Web Brows
- 美国电影超短200句
dcj3sjt126com
电影
1. I see. 我明白了。2. I quit! 我不干了!3. Let go! 放手!4. Me too. 我也是。5. My god! 天哪!6. No way! 不行!7. Come on. 来吧(赶快)8. Hold on. 等一等。9. I agree。 我同意。10. Not bad. 还不错。11. Not yet. 还没。12. See you. 再见。13. Shut up!
- Java访问远程服务
dyy_gusi
httpclientwebservicegetpost
随着webService的崛起,我们开始中会越来越多的使用到访问远程webService服务。当然对于不同的webService框架一般都有自己的client包供使用,但是如果使用webService框架自己的client包,那么必然需要在自己的代码中引入它的包,如果同时调运了多个不同框架的webService,那么就需要同时引入多个不同的clien
- Maven的settings.xml配置
geeksun
settings.xml
settings.xml是Maven的配置文件,下面解释一下其中的配置含义:
settings.xml存在于两个地方:
1.安装的地方:$M2_HOME/conf/settings.xml
2.用户的目录:${user.home}/.m2/settings.xml
前者又被叫做全局配置,后者被称为用户配置。如果两者都存在,它们的内容将被合并,并且用户范围的settings.xml优先。
- ubuntu的init与系统服务设置
hongtoushizi
ubuntu
转载自:
http://iysm.net/?p=178 init
Init是位于/sbin/init的一个程序,它是在linux下,在系统启动过程中,初始化所有的设备驱动程序和数据结构等之后,由内核启动的一个用户级程序,并由此init程序进而完成系统的启动过程。
ubuntu与传统的linux略有不同,使用upstart完成系统的启动,但表面上仍维持init程序的形式。
运行
- 跟我学Nginx+Lua开发目录贴
jinnianshilongnian
nginxlua
使用Nginx+Lua开发近一年的时间,学习和实践了一些Nginx+Lua开发的架构,为了让更多人使用Nginx+Lua架构开发,利用春节期间总结了一份基本的学习教程,希望对大家有用。也欢迎谈探讨学习一些经验。
目录
第一章 安装Nginx+Lua开发环境
第二章 Nginx+Lua开发入门
第三章 Redis/SSDB+Twemproxy安装与使用
第四章 L
- php位运算符注意事项
home198979
位运算PHP&
$a = $b = $c = 0;
$a & $b = 1;
$b | $c = 1
问a,b,c最终为多少?
当看到这题时,我犯了一个低级错误,误 以为位运算符会改变变量的值。所以得出结果是1 1 0
但是位运算符是不会改变变量的值的,例如:
$a=1;$b=2;
$a&$b;
这样a,b的值不会有任何改变
- Linux shell数组建立和使用技巧
pda158
linux
1.数组定义 [chengmo@centos5 ~]$ a=(1 2 3 4 5) [chengmo@centos5 ~]$ echo $a 1 一对括号表示是数组,数组元素用“空格”符号分割开。
2.数组读取与赋值 得到长度: [chengmo@centos5 ~]$ echo ${#a[@]} 5 用${#数组名[@或
- hotspot源码(JDK7)
ol_beta
javaHotSpotjvm
源码结构图,方便理解:
├─agent Serviceab
- Oracle基本事务和ForAll执行批量DML练习
vipbooks
oraclesql
基本事务的使用:
从账户一的余额中转100到账户二的余额中去,如果账户二不存在或账户一中的余额不足100则整笔交易回滚
select * from account;
-- 创建一张账户表
create table account(
-- 账户ID
id number(3) not null,
-- 账户名称
nam
![]()
![]() 替代式中广义积分那一项,我们叫做
替代式中广义积分那一项,我们叫做![]() 的先验:
的先验:![]()
![]() 这个等式,其实也就是分两步求解:
这个等式,其实也就是分两步求解:![]() ,通常把这一步称为预测步。
,通常把这一步称为预测步。![]() ,通常把这步称为更新步。
,通常把这步称为更新步。![]() 都服从高斯分布的话,那么这就是人们常说的卡尔曼滤波。
都服从高斯分布的话,那么这就是人们常说的卡尔曼滤波。![]() 相当于求解高斯分布的卷积;
相当于求解高斯分布的卷积;![]() 就是求解两个高斯分布的乘积,而这个计算我们在上一节便已经推导过了。
就是求解两个高斯分布的乘积,而这个计算我们在上一节便已经推导过了。![]()
![]()
![]()
![]() ,这个式子相当于一个高斯分布
,这个式子相当于一个高斯分布![]() 加上
加上![]() ,因此
,因此![]() 也满足高斯分布,所以
也满足高斯分布,所以![]()
![]()
![]()
![]() ,这个式子相当于一个高斯分布
,这个式子相当于一个高斯分布![]() 加上
加上![]() ,因此
,因此![]() 也满足高斯分布,所以
也满足高斯分布,所以![]()
![]() 必须满足高斯分布
必须满足高斯分布![]()
![]() 是符合高斯分布,所以我们在这里给定其均值方差为:
是符合高斯分布,所以我们在这里给定其均值方差为:![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 。代入
。代入![]() ,
,![]() ,
,![]() ,此处经过归一化之后,便满足概率公理了:
,此处经过归一化之后,便满足概率公理了:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()