【算法特训总结】计算机经典算法的核心思想及独特角度的解读

计算机经典算法的核心思想及独特角度的解读

---

在1月1日新年之日开始的"算法特训"(一月一日~二月十日)终于结束了,对于这本<<算法竞赛经典>>,除了第十章(在上个暑假末期的"离散数学特训"已经覆盖)和第十二章(属于进阶范围还没看)之外已经搞定了其他部分,但是仍然也有许多没明白的地方(做了标记后续讨论);在这里做一个收尾总结,肯定不求写那种流水账的知识概括,而偏重于精华思想的提取和独特角度的解读;

---

成为算法高手的11个技巧(Tricks)

在这里容许我模仿一下<>的口吻来叙述一些书里的精华思维;这些思维其实零散地分布在每一章和每一道习题里,<<算法竞赛经典>>的组织形式是数据结构基础、暴力求解法、动态规划… …这样的算法方法分章节撰写,既然它已经这样做了,这篇总结里我想将书中一些有亮点的思维用$11$个相互独立的技巧来叙述如下:

Trick 1:c++技巧

• c++技巧:c++是实现算法最顺手的一门语言,c++的技巧遍布正本书的范围,一些必要的使用方式可以大大简化算法的表达,使其清晰易读;

使用函数指针来实现导数的运算,使得其的表达是更加直观的数学语言形态:

double loss_function(VectorXd* X)
{
    return (W*(*X)).norm();
}

double derivation(double(*loss_function)(VectorXd*),VectorXd* X)
{
    VectorXd X_new;    
    X_new.array() = X->array() + step;    
    cout<<"Now the loss is:"<<loss_function(X)<<endl;    
    return (loss_function(&X_new)-loss_function(X))/step;
}

使用泛型,屏蔽底层的运算法则细节,专心编写上层的逻辑;这里举一个排序的例子,考虑如下的泛型类Node,它的加法$+$的和比较方法$>$实现细节可以用不同的法则定义,而只需要编写其排序的实现:

template<class Node>
struct node_wrap {    
        Node* ptr;
        node_wrap(Node* p = 0) : ptr(p) { }
         
        Node& operator* const { return *ptr; }
        Node* operator-> const { return ptr; }
        node_wrap& oeprator++()    
        node_wrap operator+(int)        
        bool operator== (const node_wrap& i)    
        bool operator> (const node_wrap& i)    
        bool operator!= (const node_wrap& i)
};

可以预编写一些"头"来定义一些常用的功能:比如数据类型的转换,c++可能不像很多动态语言那样一个强制类型转换就了事了,好在c++可以很方便地rename啊或者简化一些原生语句:

template<class T>inline string toString(T x) 
{
    ostringstream sout;    
    sout << x;    
    return sout.str();
}
... ...
typedef unsigned int uI;
typedef long long LL;
typedef unsigned long long uLL;
typedef queue< int > QI;
typedef priority_queue< int > PQIMax;
typedef priority_queue< int, VI, greater< int > > PQIMin;
const double EPS = 1e-8;
const LL inf = 0x7fffffff;
const LL infLL = 0x7fffffffffffffffLL;
const LL mod = 1e9 + 7;
const int maxN = 1e4 + 7;
const LL ONE = 1;
const LL evenBits = 0xaaaaaaaaaaaaaaaa;
const LL oddBits = 0x5555555555555555;

Trick 2:问题分解

• 问题分解:复杂的问题分解成若干个独立简单的问题,这是一个相当通用的思想:事实上分治法,双向搜索,降维法等等的本质都是复杂问题的分解,下面列举一些代表性问题和解决思路;

(UVa1605 - Building for UN)有$n$个国家,要求你设计一栋楼并为这n个国家划分房间,要求国家的房间必须连通,且每两个国家之间必须有一间房间是相邻的;

将这个问题分解成"两层楼的房间规划",然后令第一层第$i$行全是国家$i$,令第二层第$j$行全是国家$j$,则$\to$此时$\forall$国家$i,j$是通过两层之间相邻的;

(uva11134 - Fabled Rooks)你的任务是在$n\times n$的棋盘上放置$n$辆车,使得任意两辆车不互相攻击,且第$i$辆车在一个给定的矩形$R_i$以内;

行列可以分开考虑,它们互不影响,单单考虑行的话,其实就是给定若干个区间,然后给每个区间都分配一个点,使得点不重复的情况下都能落在相应区间中,可以对区间按右端点升序排序,右端点相等时按左端点升序排序,从左往右看每个区间,尽量往区间的左端点分配即可(问题分解+贪心法).

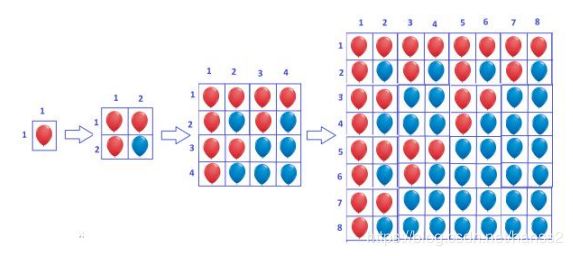
(UVA - 12627 Erratic Expansion)一开始有一个红气球.每小时后,一个红气球会变成$3$个红气球和$1$个蓝气球,而1个蓝气球会变成$4$个蓝气球.如图所示分别是经过$0,1,2,3$小时后得情况.经过$k$小时后,第$AB$行一共有多少个红气球;

由图分析,每次把图分为四个部分,右下角的部分全为蓝气球,不用去管他,剩下三部分都是一样的并且和前一小时的图形是一样的,这样的话我们可以计算出每个时刻红气球的总数.既然每次可以分为四部分,那么很明显的就是用分治法来解决.分别计算出$B$行之前和$A-1$行之前的红气球总数,那么$A\sim B$行的气球总数就是两者相减.

Trick 3:映射

• 映射:这本来是一个数学概念,但是也是一个相当通用的思想:事实上一些极其复杂并且看似难以下手的问题往往可以通过将输入映射到一个特征量来解决,下面列举一些代表性问题和解决思路;

(uva1103 - Ancient Messages)给出一幅黑白图像,每行相邻的四个点压缩成一个十六进制的字符.然后还有题中图示的6种古老的字符,按字母表顺序输出这些字符的标号(其实关键就是识别这些符号).

图像是被压缩过的,所以我们要把它解码成一个$01$矩阵.而且我们还要在原图像的四周加一圈白边,这样图中的白色背景都连通起来了.黑色连通块的个数就是字符的个数.观察题中字符样式可知,每种字符中包裹的“白洞”的个数是不同的,所以我们可以根据每个字符中的“白洞”的个数来区别这些字符.

因此核心思想是:图像$\mapsto$“白洞”的个数,“白洞”数即映射的特征量;

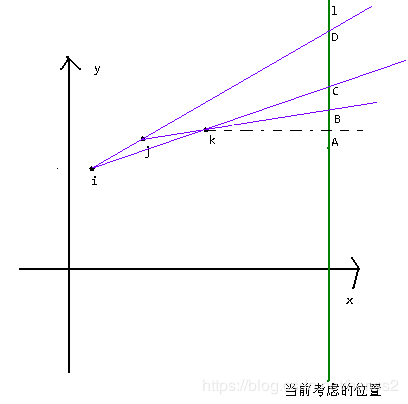
(uva1451 - Average)给出一个$01$串,选一个长度至少为$L$的连续子串,使得串中数字的平均值最大;

首先预处理子串的前缀和$S$,如果在坐标系中描出$(i,S_i)$这些点的话.所求的平均值就是两点间的斜率了,具体来说,在连续子串$[a,b]$中,有$S_b-S_{a-1}$个$1$,长度为$b-a+1$,所以平均值为$(S_b-S_{a-1})/(b-a+1)$;所以就把问题转化为:求两点横坐标之差至少为$L-1$,能得到的最大斜率.

因此核心思想是:数字的平均值$\mapsto$两点间的斜率(特征量);

(QT中的事件机制)这里谈一个题外话,但是和程序设计密切相关;信号与槽(Signal & Slot)是Qt编程的基础,也是Qt的一大创新.因为有了信号与槽的编程机制,在Qt中处理界面各个组件的交互操作时变得更加直观和简单.

信号(Signal)就是在特定情况下被映射的事件,例如PushButton 最常见的信号就是鼠标单击时映射的 clicked() 信号,一个 ComboBox 最常见的信号是选择的列表项变化时映射的 CurrentIndexChanged()信号.GUI程序设计的主要内容就是对界面上各组件的信号的响应,只需要知道什么情况下映射哪些信号,合理地去响应和处理这些信号就可以了.

槽(Slot)就是对信号响应的函数.槽就是一个函数,与一般的C++函数是一样的,可以定义在类的任何部分(public、private或protected),可以具有任何参数,也可以被直接调用.槽函数与一般的函数不同的是:槽函数可以与一个信号关联,当信号被映射时,关联的槽函数被自动执行.信号与槽关联是用QObject::connect() 函数实现的,其基本格式是:

QObject::connect(sender, SIGNAL(signal()), receiver, SLOT(slot()));

Trick 4:巧用数据结构

• 巧用数据结构:首先说明,什么BFS使用队列,处理任务使用优先队列这些传统思路不属于我们的讨论范畴,"巧用"强调的是使用简单的数据结构简化处理看似毫不相干的复杂问题(比如并查集就是巧妙联系了联通分量集合和树结构),下面列举一些代表性问题和解决思路;

(uva297 - Quadtrees)用四分树来表示一个黑白图像:最大的图为根,然后按照图中的方式编号,从左到右对应4个子结点.如果某子结点对应的区域全黑或者全白,则直接用一个黑结点或者白结点表示;如果既有黑又有白,则用一个灰结点表示,并且为这个区域递归建树.

利用递归建树,因为是4分树,所以递归时,当遇见$p$(非叶节点)就递归分别4个位置,每个位置记录左上角,再利用此次递归的边长即可得到本块的大小,边长每次缩小2倍… …其解决思路不展开细讲,巧妙的是用树结构作为黑白图像表达的方式;

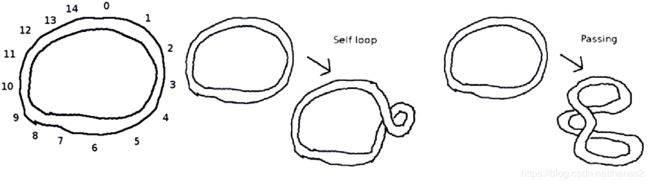
(uva1624 - Knots)给出一个橡皮筋,有两种操作,问是否可以将它还原;

初见这道题的时候很有代数拓扑的感觉,结果和高深的数学没有必然联系,其实使用"环形链表"的数据结构即可解决;先用链表把每一个节点串起来,并对有覆盖的地方进行标记.模拟解锁操作,如果一个节点和它所覆盖的节点之间没有其他结,那么进行逆self loop操作.同理进行逆passing操作.如果能把所有的结都解开,则答案是有解.

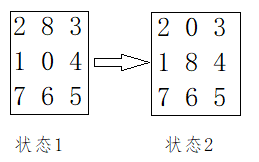
(八数码问题:借助链表的Hash来判重)在$3\times 3$的棋盘上,摆有八个棋子,每个棋子上标有1至8的某一数字.棋盘中留有一个空格,空格用0来表示.空格周围的棋子可以移到空格中.要求解的问题是:给出一种初始布局(初始状态)和目标布局,找到一种最少步骤的移动方法,实现从初始布局到目标布局的转变.

使用hash判重(参考博客https://blog.csdn.net/u012283461/article/details/79078653),将状态数字串通过某种映射$f(x)$从$012345678-876543210$这样一个大集合,映射到$128$M范围之内;这里采用简单的hash,取模一个大质数,只要这个质数大于$9!$即可;

当然这里可能出现冲突,也就是$ke{y}_1!=ke{y}_2$但是$f(ke{y}_1)==f(ke{y}_2)$,hash算法只能减少冲突不能避免冲突.这里如何减少冲突呢?挂链表,当$ke{y}_1!=ke{y}_2$但是$f(ke{y}_1)==f(ke{y}_2)$,则将key_2挂到key_1后面;

int hashTable[M];//hashtable中key为hash值,value为被hash的值 
int next[M];//next表示如果在某个位置冲突,则冲突位置存到hashtable[next[i]] 
int hash(int n)
{
       return n%N; 
}

bool tryInsert(int n)
{
       int hashValue=hash(n);      
       while(next[hashValue]) //如果被hash出来的值得next不为0则向下查找           
       {
               if(hashTable[hashValue]==n)//如果发现已经在hashtable中则返回false                  
               return false;               
               hashValue=next[hashValue];      
       }//循环结束hashValue指向最后一个hash值相同的节点        
       if(hashTable[hashValue]==n)//再判断一遍              
           return false;       
       int j=N-1;//在N后面找空余空间,避免占用其他hash值得空间造成冲突        
       while(hashTable[++j]);//向后找一个没用到的空间         
       next[hashValue]=j;      
       hashTable[j]=n;     
       return true; 
}

Trick 5:最优子结构

• 最优子结构:最优子结构严格来说不是一种"解决问题的思维",而是"一类问题具备的性质".最优子结构是依赖特定问题和子问题的分割方式而成立的条件.各子问题具有最优解,就能求出整个问题的最优解,此时条件成立.比如求广州到北京的最短距离,假设这个路径必经过中间的南京,那么先把路径分割为(广州,南京)和(南京,北京).分别求出子路径的最短距离然后再连接,就可以得到广州到北京的最短路径;下面列举一些代表性问题和解决思路;

(uva11054 - Wine trading in Gergovia)直线上有$n$个等距的村庄,每个村庄要么买酒,要么卖酒.设第$i$个村庄对酒的需求为$a_i,a_i>0$表示买酒,$a_i<0$表示卖酒,所有村庄供需平衡.把$k$个单位的酒从一个村庄运到相邻村庄需要$k$个单位的劳动力.计算所需最少劳动力.

从左边第一个开始分析,如果它卖酒,则可以把它全卖给第二个村庄,如果它买酒,可以从第二个村庄那里买酒,依次下去分析第二个直到最后一个村庄.这样的话每次买酒和卖酒的距离都是最短的,劳动力肯定也是最少的(每次只考虑最左边的村庄及其右侧村庄构成的子结构最优).

(uva348 - Optimal matrix chain multiplication)给出$N$个矩阵$(A_1,A_2,...,A_n)$,求完全括号化方案,使得计算乘积$(A_1{A}_2...A_n)$所需乘法次数最少.并输出方案.

要求的是$[0,n-1]$的最小代价.且大区间的决策依赖于小区间.矩阵连乘的最后一定有一个最后一次乘法,假设最后一个乘号在第$k$个矩阵后,也就是$P=A_1\times A_2\times ...A_k$和$Q=A_{k+1}\times A_{k+2}\times ...\times A_n$.只需分别求出$P,Q$的最优方案(最优子结构).

Trick 6:空间换时间

• 空间换时间:这句听起来像斯大林行事作风的技巧甚至被用在了微信的聊天记录搜索里(快速的Hash,用$O(n)$的空间复杂度换取至少$O(n)$的时间复杂度),下面列举一些代表性问题和解决思路,比如刷表法;

(uva1583 - Digit Generator)如果$x$加上$x$的各个数字之和得到$y$,就说$x$是$y$的生成元.给出$n(1<=n<=100000)$,求最小生成元.无解输出$0$.例如,$n=216,121,2005$时的解分别为$198,0,1979$.

可以利用打表的方法,提前计算出以$i$为生成元的数,设为$d$,并保存在a[d]中(a[d]=i),反复枚举,若是初次遇到或遇到更小的则更新(写入表);

(uva1025 - A Spy in the Metro)某城市地铁是线性的,有$n(2\le n\le 50)$个车站,从左到右编号$1\sim n$.有$M_1$辆列车从第$1$站开始往右开,还有$M_2$辆列车从第$n$站开始往左开.列车在相邻站台间所需的运行时间是固定的,因为所有列车的运行速度是相同的.在时刻$0$,Mario从第$1$站出发,目的在时刻$T(0\le T\le 200)$会见车站$n$的一个间谍.在车站等车时容易被抓,所以她决定尽量躲在开动的火车上,让在车站等待的时间尽量短.列车靠站停车时间忽略不计,且Mario身手敏捷,即时两辆方向不同的列车在同一时间靠站,Mario也能完成换乘.

状态定义:dp[i][j]:到时刻$i$的时候(出发的时候时刻为0,约定时间为时刻time),从$j$号车站开往$N$号车站,在车站等待的最少的时间.这个人当前的策略:

1.在车站等待一个单位的时间(该站此时没有发车时应该这么做);
2.坐上开往左边的火车;
3.坐上开往右边的火车;

状态转移方程(我们可以做一个乘车时刻表(空间换时间)来记录i时刻j车站是否有车经过.):

dp[i][j] = min(dp[i+1][j]+1,dp[i+t[j]][j+1],dp[i+t[j-1]][j-1]);

Trick 7:递推

• 递推:事实上计算机专业的应该在大一的离散数学/组合数学里学过递推方程,其实不光只有组合问题需要用到递推思维;下面列举一些代表性问题和解决思路,比如动态规划的状态转移思想其实也是在已知一些边界条件情况下做递推;

(uva580 - Critical Mass)有$U$和$L$两种盒子,数量足够多,要把$n$个盒子排成一行,但至少要有3个$U$放在一起,问有多少种方法.

设$f[i]$为$i$个盒子的合法方案数,$g[i]$为$i$个盒子的非法方案数.对于$f[n]$,考虑第一次出现三个U连续的情况是在$i,i+1,i+2$,则$i-1$(如果存在)必须是$L$,之前不能出现三个$U$连续,之后随便选.总方案数为$g[i-2]\ast 2^{(n-i-2)}$.另外在特殊处理一下$i-1$不存在的情况,即$i=1$,此时的方案数为$2^{(n-3)}$. 综上所述,$f[n]=2^{(}n-3)+{\sum }_{i=2...n-2}g[i-2]2^{(n-i-2)}$,$g[n]=2^n-f[n]$;

(uva12034 - Race)两匹马比赛有三种比赛结果,求$n$匹马比赛的所有可能结果总数;

现在设$i$匹马占有$j$个名次,问所有可能的情况;dp[i][j]表示$i$匹马占有$j$个名次的组合情况,然后考虑$i$匹马和$i+1$匹马的关系(也就是多了一匹马要放在哪个位置)这匹马和前$i$匹马中至少一匹马的成绩相同($j$个名次就有$j$种情况),这匹马独占了一个成绩(可以放入$j$个位置)所以可以得到递推式:

dp[i][j] = dp[i-1][j] * j + dp[i-1][j-1] * j;

Trick 8:剪枝

• 剪枝:剪枝不仅仅针对有关树结构出现的问题,一切有关状态空间搜索的问题,包括但不仅限于贪心法、回溯法、动态规划、图算法等都会用到剪枝;简单来说就是及时检查,来停止某个分支方向的搜索,来避免不必要的搜索浪费(有"及时止损"的感觉);下面列举一些代表性问题和解决思路;

(uva140 - Bandwidth)输入一行数据,其中有$n$个字符节点和节点间的连通关系,输出一组排列,节点$i$的带宽为$i$和相邻节点在排列中的最远距离,所有带宽的最大值就是该排列的带宽.按字典序输出带宽最小的排列.

思路(参考博客https://www.cnblogs.com/luruiyuan/p/5847706.html):
1.建立双射关系(回忆映射思维):从字符A到字符Z遍历输入的字符串,用strchr函数将输入中出现的字符找出,并将找出的字符进行编号,用letter和id分别存储字符和对应的编号;
2.降维:输入中给出的,是类似于邻接表形式的二维形式,如果我们用二维数据结构,将增加处理时对于输出细节的处理难度,用2个vector将输出降低到1维,简化了计算Bandwidth时的代码,实际上让我们更加有的放矢;
3.存储必要信息,位置:数组pos每个下标代表字母编号,存储的是对应的位置下标,便于计算时寻找位置;
4.剪枝:减去不必要的计算(虽然对于本题而言不是必须的);

(uva1354 - Mobile Computing)就是首先给一个房间的宽度$r$,之后有$s$个挂坠,第$i$个挂坠的重量是$w_i$,设计一个尽量宽,但是不能宽过房间的宽度;

(主要关注一下如何判重来剪枝)自顶向下,把集合分为左右子集(分别为左右子树所含的挂坠集合),在递归调用左右子集.枚举子集的思路用的是二进制枚举集合的思路,每个二进制数分别对应挂坠集合能组成的所有天平的左右臂长度,用vector node[MAXN]储存,[]内是二进制数.还用到了二进制&,^运算来处理集合间的关系.

(uva690 - Pipline Scheduling)有一台包含$5$个工作单元的计算机,还有10个完全相同的程序需要执行.每个程序需要$n(n<20)$个时间片来执行,可以用一个$5$行$n$列的保留表(reservation table)来表示,其中每行代表一个工作单元(unit0~unit4),每列代表一个时间片,行$i$列$j$的字符为$X$表示“在程序执行的第$j$个时间片中需要工作单元$i$”.例如,如图所示就是一张保留表,其中程序在执行的第$0,1,2,...$个时间片中分别需要unit0,unit1,unit2…同一个工作单元不能同时执行多个程序,因此若两个程序分别从时间片$0$和$1$开始执行,则在时间片$5$时会发生冲突(两个程序都想使用unit0),如图所示.输入一个$5$行$n(n<20)$列的保留表,输出所有$10$个程序执行完毕所需的最少时间,例如,对于图中的保留表,执行完$10$个程序最少需要$34$个时间片.

使用二进制表达压缩状态,加上剪枝:每次移动只需要判断原来的状态向后移与程序的保留表是否有冲突,如果没有,将这两个取并作为新的状态(我最后看明白的办法是做表记录那些程序间的间距时间是可行的,然后对不可行的方案剪枝);

Trick 9:仿真/演绎

• 仿真/演绎:仿真/演绎思想其实是两个对立的但互相依存的思维,"仿真"是针对无从下手的复杂问题,但是知道有限的边界条件,于是把握其中的规则来编写仿真过程求解;"演绎"思想是能通过问题很好地预知很多过程,这时就可以剔除很多不必要的分支可能,针对性编写程序;

(uva1609 - Foul Play)给一群队伍,队伍$1$至少能击败一半的队伍(令为白队),且不能击败另外的队伍(令为黑队),每只队伍$1$不能击败的黑队都有另一只白队能击败他.给一个比赛安排让一号队夺冠;

(这个题目属于中间过程的可推导性比较好的,因此可以使用构造思维求解)构造之后的递归就相对比较简单了.构造的方式分为四个阶段(能够证明按照这样的策略打过一轮之后,剩下的队伍还满足初始条件,因此可以递归求解):
1.把满足条件的队伍A和B配对,其中队伍$1$打不过A,队伍$1$能打过B,并且B能打过A.
2.把队伍$1$和剩下的它能打过的队伍配对.
3.把队伍$1$打不过的队伍相互配对.
4.把剩下的队伍配对.

(uva10603 - Fill)设$3$个杯子的容量为$abc$,起初只有第三个杯子装满了$c$升水.其它两个杯子均为空.最少要倒多少升水可以让某一个杯子里有$d$升水.如果无法做到$d$升水.就让某个杯子里有$d^{\prime }$升水,其中$d^{\prime }<d$而且尽量接近$d(1\le a,b,c,d\le 200)$要求输出最小的倒水量和目标水量($d$或者是$d^{\prime }$);

(这道题和上一题相反,难以推测其中的事件细节,适合仿真地解决;据说是美团的算法岗面试题)使用广度优先搜索BFS,可以解决状态转移或者是决策问题.而这道题$3$个杯子,假设在某一时刻第一个杯子里有$v_1$升水.第二个杯子有$v_2$升水,第三个杯子有$v_3$升水.而这个时候可以说是在某一时刻的状态为$(v_1,v_2,v_3)$,而每个状态之间都可以通过某种方式进行转换,也就是在状态图$G$中进行BFS;这道题就是通过倒水转移.

Trick 10:归约

• 归约:归约思想是逻辑学里的一个概念(归约是使用解题的"黑盒"来解决另一个问题的思维方式),就是将问题$A$转变为问题$B$;其好处是可以把一个陌生的问题转换为一个已经有成熟固定套路的解法的问题(在图论问题中尤为常见);

(uva753 - A Plug for UNIX)有若干个电器设备需要不同的适配器才能接上电源,现在你要让尽可能多的电气设备接上电源.首先你手中有$n$个适配器和适配器的型号,再告诉你有$m$个电器和他们分别对应的适配器的型号,最后还有一个商店提供买不同型号的适配器转换器,转换是单向的$A\to B$表示能把$A$接口转换成$B$接口(就是原来需要用$A$适配器的现在可以用$B$适配器当然也可以用原来的不变)超市提供的转换器数量是没有限制的,可以无限买.

节点表示插头类型,边表示转换器,然后使用floyd算法,计算出任意一种插头类型能否转换成另外一种插头类型.额外添加一个源点$s$,从$s$到设备device[i]连接一条容量为$1$的边,再额外加一个汇点$t$,从插座target[i]到$t$连接一条容量为$1$的边.然后只要device[i]能够转换成target[i]就在两者间添加一条容量为INF的边,表示允许任意多设备从device[i]转换成target[i].最后求s-t最大流(规约),m减去最大流就是所要求的答案.

(uva247 - Calling Circles)如果两个人互相打电话(直接或间接),则说他们在同一个电话圈里.例如,a打给b,b打给c,c打给d,d打给a,则这四个人在同一个电话圈里;如果e打给f但f不打给e,则不能推出e和f在同一个电话圈里.输入$n(n\le 25)$个人的$m$次电话,找出所有的电话圈.人名只包含字母,不超过$25$个字符,且不重复.

用map存下人名,然后用floyd算法跑一遍连通性就行了.因为floyd算法是解决任意两点之间的最短距离,这里我们可以用此特性来判断连通性(归约为求$\forall$两点之间最短路).

Trick 10:谓词

• 谓词:谓词也是现代逻辑学里的一个概念(归约是使用解题的"黑盒"来解决另一个问题的思维方式),在这本书里这是最核心的一个思维(前文中很多方法也有这个思维的影子),一切状态和描述状态的本质都是谓词,可以说除了绝对静态的概念(比如时间,整数…)外"一切都可以看作谓词"(在动态规划中尤为常见,状态描述函数就是谓词,而状态转移方程其本质就是谓词的动态作用),在这里我还不想把它说得太抽象,下面看一些例子(可以看出不同描述方法的谓词函数的选取和谓词描述范围因素(也就是状态函数的维度)会对问题的解决产生决定性影响);

(uva12186 - Another Crisis)一个公司有$1$个老板和$n$个员工,$n$个员工中有普通员工和中级员工,现在进行一次投票,若中级员工管理的普通员工中有$T\%$的人投票,则中级员工也投票并递交给上级员工;求最少需要多少个普通员工投票,投票才能到达老板处;

用一个vector存储结点的子节点,设f[i]表示(谓词函数)为了让信息传到$i$,需要的最少人数;设结点$u$的子节点有$k$个,则至少需要人数:

$$c=(k\ast T-1)/100+1$$

把所有的子结点的f[i]值排序,选最小的$c$个加起来就是当前点的"最少需要员工投票数量";

(uva1220 - Party at Hali-Bula)公司的员工成树形分布,每个人只有一个直属上司,现在要开个party,不能让一个人和他的直接老板同时出现在party上,问最多能选多少人,并问选择是否唯一;

用dp[i][j]表示最大人数(谓词函数),其中$i$为第$i$个点,其中$j$可以为$0$或者为$1$,表示第$i$个人选或者不选,即选或者不选$i$的以$i$为根的子树的最优值,另一个f[i][j]表示选择唯不唯一,$i$和$j$的含义dp数组一样;那么只需要写出状态转移的细节即可(考察节点$u$):

void dpp(int u)
{
    if(v[u].empty())
    {
            dp[u][1]=1;        
            dp[u][0]=0;        
            return ;   
    }    
    int son=v[u].size();    
    for(int i=0;i<son;i++)
    {
            int to=v[u][i];
            dpp(to);        
            dp[u][1]+=dp[to][0];        
            if(dp[to][0]>dp[to][1])
            {
                dp[u][0]+=dp[to][0];            
                if(f[to][0]==0) f[u][0]=0;        
            }else
            {   dp[u][0]+=dp[to][1];            
                if(f[to][1]==0) f[u][0]=0;            
                if(dp[to][0]==dp[to][1]) f[u][0]=0;        
            }    
     }    
     dp[u][1]++;
}

---

11个技巧(Tricks)的数学内涵

• c++技巧:和数学有任何关系吗?泛型屏蔽底层运算细节规则的设定,是不是和群论里忽略底层加法运算规则但是抽象出代数结构和对称性的思想有异曲同工之妙?

• 问题分解:用贝叶斯思想考察问题$Q$,其因果描述可以写作$\mathbb{P}(Q|q_1,...,q_n)$,其中$q_1,...,q_n$是$n$个解决问题的关键考察因素,那么问题可以独立拆分为$\mathbb{P}(Q|q_i)$的形式当前仅当$\mathbb{P}(Q|q_1,...,q_n)={\prod }_i\mathbb{P}(Q|q_i)$;

• 映射:映射的思维本质是抽象对应,在解决问题中通过构造"映射"往往能够简化问题;
  一些有意义的特定的映射是:

函数:表示为$y=f(x)$,把具有元素$x$的标量空间$X$映射到具有元素$y$的标量空间$Y$;
泛函:表示为$\rho =\varphi (f)$,把具有元素$f$的函数空间映射到具有元素$\rho$的标量空间$A$(函数集合到数集上的映射:定义域为函数,而值域为实数的"函数");
算子:表示为$g=L(f)$,把一个函数空间映射到自己中,即$f,g$是同一函数空间的元素(函数空间到函数空间上的映射$O:X\to X$.广义上的算子可以推广到任何空间,如内积空间等);

• 巧用数据结构:合理的数据结构的套用本质上是一种数学建模;

• 最优子结构:当且仅当局部最优解是蕴含($\Rightarrow$)全局最优解时可以用最优子结构看待问题;

• 空间换时间:构造一个表$T(x)=f(x)$来缓存每次要计算的和$x$相关的函数值$f(x)$即为该思想的形式化描述;

• 递推:当$f_n=F(f_{n-1},...,f_1)$形式的关系成立时,可以用递推的思维解决关于$f_i$这样的函数所描述的问题;

• 剪枝:当沿着分支$i$进行下去的搜索"不划算时",也就是$f_i+{\hat{L}}_i>\tilde{L}$时,终止这个分支的搜索;其中$f_i$是沿着分支$i$进行到当前的代价值,${\hat{L}}_i$是沿着$i$搜索下去最乐观的代价(一般需要估计一个下界),$\tilde{L}$是当前全局最优代价;

• 仿真/演绎:当我们无法洞悉问题$Q$的内部状态集合$\{s_i\}$时,我们可以构建一个根据问题规则描述的作用$f(\cdot )$,从状态$s_0$开始用$f(0)$作为初始开始仿真并记录下状态集合$\{s_i\}$;

• 归约:归约其实是理论计算机里计算复杂度的一个概念;假设有一个复杂的问题$P$,而它看起来与一个已知的问题$Q$很相似,可以试着在两个问题间找到一个归约(reduction,或者transformation),记作$P\prec Q$.对于问题的先后,归约可以达到两个目标:

i) 已知$Q$的算法,那么就可以把使用了$Q$的黑盒的$P$的解决方法转化成一个$P$的算法.

ii) 如果$P$是一个已知的难题,或者特别地,如果$P$的下限,那么同样的下限也可能适用于$Q$.前一个归约是用于获取$P$的信息;而后者则是用于获取$Q$的信息.

• 谓词:考虑这样一个代数结构$(p_i,{\odot }_j,x_l)$,其中$1\le i\le n,1\le j\le m,1\le l\le k$,且$p_i\in P,{\odot }_j\in O,x_l\in X$,满足:

i) $p_i(x_1...x_c)$是一个映射:$x_1...x_c\mapsto x_d\in X$;
ii) $p_i{\odot }_j{p}_l\in P$;
iii) 存在$p_e\in P$,满足对$\forall p_i,{\odot }_j$有$p_i{\odot }_j{p}_e=p_i$;

我们将其称之为一个谓词结构(这是笔者初步构思的一个可以解决一些实际问题的代数结构);

---

总结

即使在经历了如此多的有意义的之后,我还是感到知识上的信心不足,但是好在我觉得我至少具备不错的学习能力;算法的训练后,在计算机算法方面(我们会尝试参加比赛)算是至少入门了,接下来几年大量的训练必不可少;

从明天开始我将转入一个桌面仿真软件的开发(QT c++),那将会持续到二月底,顺便我会持续阅读一些数学书;在稍早些时候(2017年的夏天)我开发了一些Linux上的期货交易算法程序,是时候结合新的数学思维和计算机编程能力重回那个战场,找回一些失落的希望了;