Python模拟财富分配实验
简介
在知乎上看到了一个模拟财富分配的实验，通过Python进行模拟实验，尽管与知乎上面的结论不太一致，但还是写出来，毕竟是实验的真实数据。
规则
在一个封闭的房间里，有一百人，每个人有100元，每个人拿出一元钱，随机给另一位人（包括自己），所有人获得这个一块钱的概率相等，反复进行实验，最后这一百个人的财富分布到底会是怎样的？
代码模拟
环境
Python 3.5
matplotlib 库
windows10 CMD运行
初始化
给100人每人100元，用Python的字典数据结构来表示，编号0-99，作为key，初始每个人的value为100.
people={}
#初始财富分配，每人100元
for i in range(0,100):
people[i]=100
一次完整分配
接下来写一个财富分配函数，进行每次的随机资金流动，对每个人都进行一次财富值减一操作，并且随机分配给其他人（包括自己，如果把自己的财富重新分配给自己，虽然自身财富值没有增长，但是可能会拉动GDP，生活中不赔不赚的事情也很常见）
我们暂且先设定，当一个人财富值为0时候，不再进行财富支出，但是不影响他获得其他人财富的概率
def assign():
for key in people.keys():
#如果财富值为0，不再流出，但是同样可以和其他人有同样的机会获取财富
if people[key]<=0 :
continue
#在0-99编号中随机选取一位
n=random.randint(0,99)
#每人从自己财富中-1
people[key]=people[key]-1
#每个人自己财富+1的机会相等
people[n]=people[n]+1
#print(key,":",people[key])
理想状态进行模拟
一个人，假设从20岁开始算起，到65岁退休，这段时间内，每天进行一次上述过程，那么就是365*（65-20）次。
for i in range(365*(65-20)):
#从20岁开始到65岁退休，每天进行一次资金流动
assign()统计结果
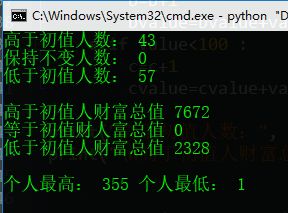
简要统计一下，比初始值低的人数和高于初始值的人数，最终的最低值哈最大值，以及100人财富的总体分布情况。
#高于，等于，低于初始值人数
a,b,c=0,0,0
#高于，等于，低于初始值人财富值总和
avalue,bvalue,cvalue=0,0,0
for value in people.values():
if value>100:
a=a+1
avalue=avalue+value
elif value==100:
b=b+1
bvalue=bvalue+value
elif value<100 :
c=c+1
cvalue=cvalue+value
print("高于初值人数：", a,"\n保持不变人数：", b, "\n低于初值人数：",c )
print("\n高于初值人财富总值",avalue,"\n等于初值财人富总值",bvalue,"\n低于初值人财富总值",cvalue)
number=list(people.keys())
wealth=list(people.values())
#wealth.sort()
print("\n个人最高：",max(wealth),"个人最低：",min(wealth))
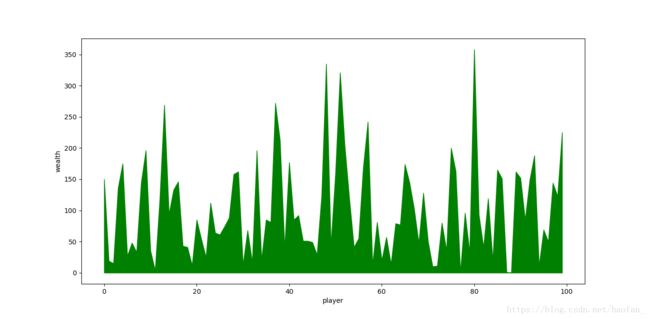
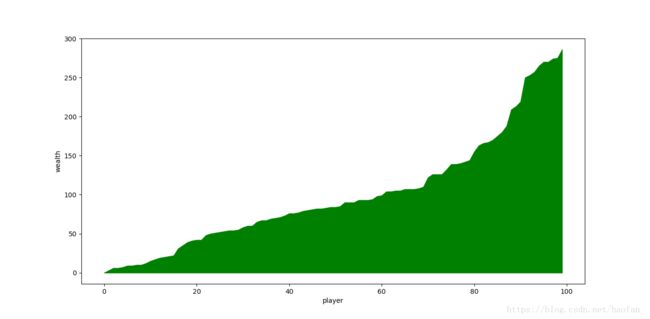
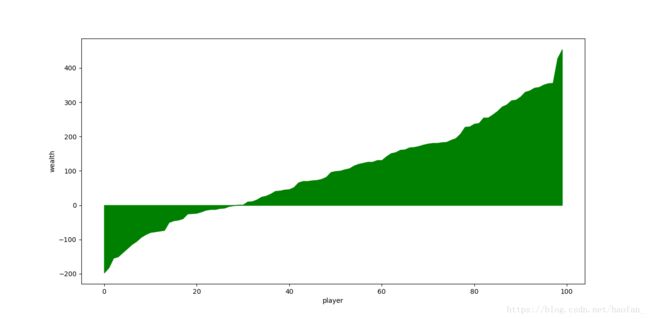
使用matplotlib进行画图显示
plt.fill_between(number,wealth,0,color='green')
plt.xlabel('player')
plt.ylabel('wealth')
plt.show()实验结果
CMD窗口输出结果
百人财富分布图
对财富值进行排序后如下
附加
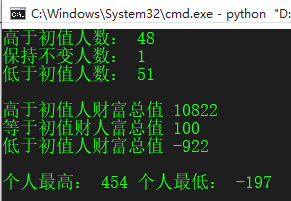
上面模拟实验，假设当财富值为0是，不再进行支出，如果修改为，可以进行支出（通过借贷继续进行，总资产为负），并且其他概率和其他人一样的情况下，在进行模拟实验，注释如下代码
#如果财富值为0，不再流出，但是同样可以和其他人有同样的机会获取财富
#if people[key]<=0 :
#continue得到实验结果为
总结
在看似最公平的情况下，大家的财富值也不会在一个平均水平，反而差距比较大，在允许透支消费情况下，贫富差距更大，两极分化严重，多次模拟资金流动后，仍然能够停留在当初财富初始值的人几乎没有，逆水行舟，不进则退，与君共勉。