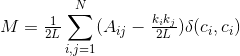Graph Community Detection
先贴出我借鉴的博客
- https://blog.csdn.net/gaofeipaopaotang/article/details/80094656
Graph Community Detection(图团体检测)
当我们的样本以及样本之间的关系可以被表示为一个网络或图(graph)时,可能存在这样的需求:我们想找出来网络中联系比较”紧密”的样本。举个例子,在社交网站中,用户以及用户之间的好友关系可以表示成下面的无向图,图中的顶点表示每个用户,顶点之间的边表示用户是否为好友关系:
直观上我们可以看出a,b,e,f之间的关系比较密切,c,d,g,h之间的关系比较密切,而这两个集合之间的关系就不那么密切了。这个例子涉及的数量规模比较小,在更大的数据上我们就不太容易人工的找出这些关系密切的集合了,那么如何通过算法把我们的用户按照关系的密切程度划分成一个个集合呢,这就是图团体检测算法要完成的工作。
图团体(graph community): 通常被定义为一种顶点(vertice)的子集,每个子集中的顶点相对于网络的其它顶点来说要连接得更加紧密。
我们将上图的社交网络表示成邻接矩阵的形式:
| - | a | b | c | d | e | f | g | h |
|---|---|---|---|---|---|---|---|---|
| a | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| b | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| c | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| d | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| e | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| f | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| g | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| h | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
1表示两用户是好友关系,0则表示不是好友关系。
顶点的度(degree):表示有多少个顶点与其相连,通常标记为k.
模块性(modularity):定义为如下公式,它是衡量图团体划分质量的一种标准,划分的越好,M的值越大。
其中L表示图包含的边的数量,N表示顶点数量,![]() 表示顶点i的度(degree),
表示顶点i的度(degree),![]() 的值为邻接矩阵中的值,
的值为邻接矩阵中的值,![]() 表示顶点i的聚类,
表示顶点i的聚类,![]() 则是克罗内克函数(Kronecker-delta function),函数的逻辑很简单,两个参数相等则返回1,不等则返回0。所以如果顶点i,j属于同一聚类,则
则是克罗内克函数(Kronecker-delta function),函数的逻辑很简单,两个参数相等则返回1,不等则返回0。所以如果顶点i,j属于同一聚类,则![]() 返回1,不属于同一聚类则
返回1,不属于同一聚类则![]() 返回0.
返回0.
首先我们把用户随机的划分成两类,如下图:
我们按照公式来计算一下这种划分方式下网络的模块性,按照公式,我们首先计算求和项,计算出每一对顶点对模块性的贡献值,我们只需要计算同一类的顶点对,应为根据![]() 函数不同类顶点对的贡献值是0:
函数不同类顶点对的贡献值是0:
| - | a(3) | b(4) | c(3) | d(3) | e(3) | f(3) | g(4) | h(3) |
|---|---|---|---|---|---|---|---|---|
| a(3) | 0 | 0 | 0 | 0-3*3/26=-0.35 | 0 | 1-3*3/26=0.65 | 0-3*4/26=-0.46 | 0 |
| b(4) | 0 | 0 | 0-3*4/26=-0.46 | 0 | 1-3*4/26=0.54 | 0 | 0 | 0-3*4/26=-0.46 |
| c(3) | 0 | 0-3*4/26=-0.46 | 0 | 0 | 0-3*3/26=-0.35 | 0 | 0 | 1-3*3/26/=0.65 |
| d(3) | 0-3*3/26=-0.35 | 0 | 0 | 0 | 0 | 0-3*3/26=-0.35 | 1-3*4/26=0.54 | 0 |
| e(3) | 0 | 1-3*4/26=0.54 | 0-3*3/26=-0.35 | 0 | 0 | 0 | 0 | 0-3*3/26=-0.35 |
| f(3) | 1-3*3/26=0.65 | 0 | 0 | 0-3*3/26=-0.35 | 0 | 0 | 0-3*4/26=-0.46 | 0 |
| g(4) | 0-3*4/26=-0.46 | 0 | 0 | 1-3*4/26=0.54 | 0 | 0-3*4/26=-0.46 | 0 | 0 |
| h(3) | 0 | 0-3*4/26=-0.46 | 1-3*3/26/=0.65 | 0 | 0-3*3/26=-0.35 | 0 | 0 | 0 |
矩阵内所有元素求和,除以2L得到模块性值:
M = −1.306/2L = −1.306/26 = −0.05
然后我们按照我们观察的结果,按照”感觉上”联系是否密切来划分:
然后同样首先计算求和项:
| - | a(3) | b(4) | c(3) | d(3) | e(3) | f(3) | g(4) | h(3) |
|---|---|---|---|---|---|---|---|---|
| a(3) | 0 | 0.54 | 0 | 0 | 0.65 | 0.65 | 0 | 0 |
| b(4) | 0.54 | 0 | 0 | 0 | 0.54 | 0.54 | 0 | 0 |
| c(3) | 0 | 0 | 0 | 0.54 | 0 | 0 | 0.54 | 0.65 |
| d(3) | 0 | 0 | 0.54 | 0 | 0 | 0 | 0.54 | 0.65 |
| e(3) | 0.65 | 0.54 | 0 | 0 | 0 | 0.65 | 0 | 0 |
| f(3) | 0.65 | 0.54 | 0 | 0 | 0.65 | 0 | 0 | 0 |
| g(4) | 0 | 0 | 0.54 | 0.54 | 0 | 0 | 0 | 0.54 |
| h(3) | 0 | 0 | 0.65 | 0.65 | 0 | 0 | 0.54 | 0 |
M = 12.22/2L = 12.22/26 = 0.47
归一化因子2L将模块性的上限值设置成了1。模块性接近或小于0表示该网络的当前聚类没有用处。模块性越高,该网络聚类成不同团体的程度就越好。通过是模块性最大化,我们可以找到聚类该网络的最佳方法。
具体过程:
- 每个顶点自己的独自构成一个聚类,然后计算整个网络的模块性M;
- 尝试选择两个聚类融合到了一起,计算由此造成的模块性改变ΔM。
- 取ΔM出现了最大增长的两个聚类进行融合。然后为这个聚类计算新的模块性 M,并记录下来。
- 不断重复第2步和第3步,每一次都融合一对聚类,得到ΔM的最大增益,然后记录新的聚类模式及其相应的模块性M。
这样,直到所有的顶点都被分组成了一个聚类时为止。然后该算法会检查这个聚类过程中的所有记录,然后找到其中返回了最高M值的聚类模式,这就是算法得到的聚类结构。