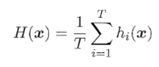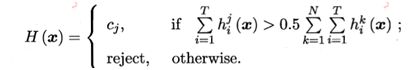高级算法梳理-Task1 集成学习及随机森林算法

本文依据周志华西瓜书及多个相关博文总结而成.

集成学习(ensemble learning) 通过构建并结合多个学习器来完成学习任务,其组成结构是:先产生一组个体学习器 individual learning 再用某种策略将他们结合起来.

集成学习通过将多个学习器进行结合,常可获得比单一学习器显著优越的泛化性能.要获得好的性能,学习器应该好而不同,学习器要有一定的准确性,不能太坏 否则集成起负作用,个体学习器还要有多样性(diversity),之间具有差异,否则集成不起作用.

集成学习两大类：Boosting个体学习器之间强依赖，必须串行生成的序列化方法.Bagging和随机森林（RandomForest）个体学习器之间不存在强依赖，可以同时生成的并行化方法。

个体学习器就是用训练数据用一个已有的算法训练产生.

同质(homogeneous)指一组个体学习器中所有学习器的类型相同.同质集成中的个体学习器称为基学习器 (base learner) 相应的学习算法称为基学习算法 (base learning algorithm) .

异质(heterogenous)指集成的个体学习器不同.异质集成中的个体学习器的学习算法不同, 其中的个体学习器也称为组件学习器(component learner).

Boosting是一族将弱学习器提升为强学习器的算法

工作机制:先从初始训练集中训练出一个基学习器，根据基学习器表现对样本进行调整，提高在训练集中做错的样本的关注来训练下一个基学习器。重复进行直到基学习器数目达到事先指定的值T，最终将T个基学习器进行加权结合

存在问题:在训练的每一轮都要检查当前生成的基学习器是否满足基本条件,检查当前基分类器是否是比随机猜测好,一旦条件不满足,则当前基学习器即被抛弃且学习过程停止,初始设置的学习轮数T也许远未达到,可能导致包含很少的基学习器而性能不佳.

解决方法:采用重采样,可获得重启动机会以避免训练过程过早停止,即在抛弃不满足条件的当前基学习器后,根据当前分布重新对训练样本进行采样,再基于新的采样结果重新训练出新的基学习器.

Boosting主要关注偏差.代表算法是AdaBoost.

关于AdaBoost算法详情参考博文<Adaboost算法原理分析和实例+代码（简明易懂)>

Bagging 采用自助采样法(bootstrap sampling)即放回采样,有的样本多次出现.采样出T个含m个训练样本的采样集(初始训练集中约有63.2%的样本出现在采样集T中，剩下的约36.8%的样本可作为验证集),然后基于每个采样集训练出一个基学习器,再将这些基学习器进行结合.

Bagging复杂度为T(O(m)+O(s)), 其中采样与投票/平均过程的复杂度O(s)很小，T是一个不大的常数，Bagging集成与直接使用基学习算法训练一个学习器的复杂度同阶，因而高效。

Bagging主要关注降低方差，在不剪枝决策树、神经网络等易受样本扰动的学习器上效用更为明显。

结合策略

学习器结合的好处：

(1)统计的原因：如果有多个假设在训练集上达到同等性能，使用单学习器可能因误选而导致泛化性能不加，结合多个学习器可以减小该风险.

(2)计算的原因：学习算法会陷入局部极小，而局部极小有可能导致泛化性能差，结合多个学习器降低陷入糟糕局部极小点的风险.

(3)表示的原因：某些学习任务的真实假设不在当前学习算法的假设空间中，此时使用单个学习器肯定无效。结合多个学习器可以扩大相应的假设空间，有可能学到更好的近似。

平均法： 简单平均,加权平均

其中wi是个体学习器hi的权重（>=0）.加权平均法未必一定优于简单平均法。在个体学习器性能相差较大时宜使用加权平均法，性能相近时宜使用简单平均法.

投票法:

绝对多数投票法（majority,voting）:

即某标记投票数过半，则预测为该标记，否则拒绝。

相对多数投票法（plurality voting）:

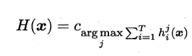预测为得票最多的标记，若同时有多个标记获得最高票，则从中随机选取一个。

加权投票法（weightedvoting）:

学习法:通过另一个学习器（次级学习器或元学习器（meta-learner））来结合多个学习器（初级学习器）。其代表Stacking.

Stacking先从初始数据集训练处初级学习器，然后“生成”一个新数据集用于训练次级学习器，在这个新数据集中，初级学习器的输出被当作样例输入特征，而初始样本的标记仍被当做样例标记。

注意点：若直接使用初级训练集来产生次级训练集，则过拟合风险会比较大。一般通过使用交叉验证或留一法。

随机森林（RandomForest）:是以决策树为基学习器构建Bagging集成的基础上，进一步在决策树的训练过程中引入了随机属性选择。

随机森林和Bagging区别：传统决策树在选择划分属性时是在当前结点的属性集合（假定有d个属性）中选择一个最优属性，而在随机森林中对基决策树的每个结点，先从该结点的属性集合中随机选择一个包含k个属性的子集，在从中选择一个最优属性用户划分。参数k控制了随机性的引入程度：若令k=d，则基决策树的构建与传统决策树相同。若令k=1，则随机选择一个属性用于划分。推荐k=log2d。Bagging中基学习器的多样性来自样本扰动（对初始训练集放回采样），随机森林中基学习器的多样性不仅来自样本扰动，还来自属性扰动。若随机森林中只包含一个个体学习器，性能有所降低。随着个体学习器增多，泛化性能更好。随机森林的训练效率优于Bagging。Bagging使用的是确定型决策树，选择划分属性时要对所有结点的所有属性进行考察。随机森林使用的随机性决策树则只需考察一个属性子集。

关于随机森林算法详情可参考博文<[Machine Learning & Algorithm] 随机森林（Random Forest）>