一般图最大匹配——带花树算法 学习小记

Text

一般图的最大匹配仍然是基于寻找增广路的

增广路的定义是这样的一条路径，它不经过重复的点，并且路径两端均没有匹配，且整条路径是非匹配边-匹配边-非匹配边这样交错的。

类比二分图最大匹配的增广路算法，如果我们找到了一条增广路，那么将这条增广路的边取反（匹配的变成非匹配，非匹配的变成匹配），那么匹配数会恰好+1，如果全图不存在增广路，也就说明当前已经是一个最大匹配了。（证明略）

一般图和二分图的区别就在于有没有边数为奇数的环
那为什么一般图最大匹配不能直接像二分图那样做呢？

考虑我们寻找增广路的过程
（图片引自 陈胤伯《浅谈图的匹配算法及其应用》，2015年国家集训队论文集）

我们在寻找增广路的时候，会将路径上的点黑白染色，匹配只存在黑点与白点之间。

如果没有环或者只有偶环，那么每个点的颜色（或者说奇偶性）是确定的
但如果出现了奇环，那么点的颜色就不再确定，因为奇环顺时针走一圈和逆时针走一圈的结果是不同的。

怎么办呢？

这就有了我们的带花树算法（名字我觉得很迷）

我们按照算法流程来一步步说明

仍然是从每个未匹配的点开始寻找增广路，不过我们采用BFS的方式，每个点均设为无色，端点染成黑色
设当前点为u（黑色）,枚举与它相邻的点v

考虑v是否已经被访问过

若v尚未访问过（v为无色）
如果v尚未匹配，说明我们找到了一条增广路，直接返回修改。
如果v已经匹配，那么将v染成白色，v的匹配点x加入队列，继续寻找增广路，x染成黑色。

容易看出，根据上面的过程，我们只会对于黑点枚举出边，正确性是显然的，并且我们访问的路径形成了一棵黑白点交错的树。

若v已经访问过（有颜色），说明我们找到了一个环。
如果它是一个偶环（v为白色），那么v显然已经被找过了，无需再找一次。

如果它是一个奇环（v为黑色），这就出锅了
怎么办呢？

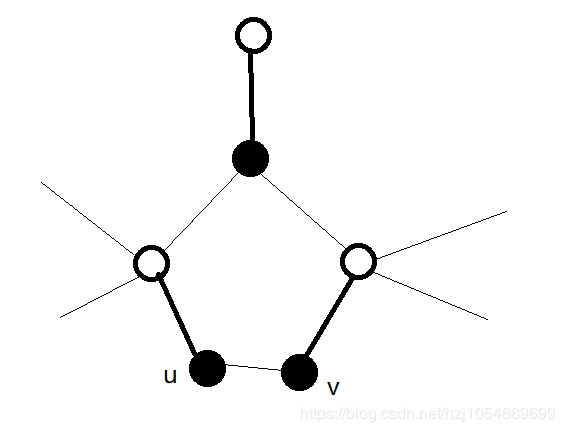
如上图，粗边为匹配边。
对于一个奇环，我们一定是从一个黑点进入，然后也在黑点碰头(u,v)，（这个可以画图理解一下，如果不是从黑点进入，我们在之前访问这个奇环时一定还没有绕一圈就找到增广路增广了）

问题在于，此时对于整个奇环的颜色都不确定了，我们令这个奇环的顶点为最顶上的那一个黑点，那么考虑u上方的这一个白点，我们既可以走从顶点走一条非匹配边到它，它作为一个白点，也可以从另一边转一圈到它，此时这个它变成了黑点，它是需要加入队列继续走的

也就是说，对于一个奇环，它上面的点都可以成为黑点。
继续观察可以发现，整个奇环的匹配状态只与顶点的匹配状态有关，如果在后来的某一次寻找时奇环上的匹配被改变了，那么顶点的颜色唯一决定了整个环的匹配边是如何走的。

也就是说，整个环就可以用一个顶点表示了，也就意味着我们可以将这个环缩掉，缩掉的环就称为“花”，缩环就是开花

我们不妨对于每一个白点x，记pre[x]表示x是由哪一个黑点走过来的，也就是记录了增广路上的非匹配边。
对于每一个点，记match[x]表示x的匹配点是谁。

缩环具体怎么缩呢？

如果直接修改原本的连边比较麻烦，我们考虑采用并查集，记录每个点所在的奇环的顶点，初始时就是它自己。缩环的时候，我们直接将环上的所有点并查集父亲连向奇环的顶点，并将环上的白点都变成黑点，并且加入队列。

此外，由于奇环可以双向走，因此我们的pre边也要变成双向的。

容易发现，我们有可能经过了多次缩环，也就是说某一次缩环的一个点很有可能是缩过的一个环顶，我们在缩环以及找到增广路返回修改的时候是需要走原来缩之前的环的，这个只需要沿着pre和match一直走即可，pre在这里相当于记录了缩掉的环内部的走法。

现在我们来理一理思路

从每个未匹配的点BFS寻找增广路，每个点均设为无色，端点染成黑色
枚举与当前点u（黑色）相邻的点v

考虑v是否已经被访问过

若v尚未访问过（v为无色）
如果v尚未匹配，找到了一条增广路，直接返回修改。
如果v已经匹配，将v染成白色，将v的匹配点x加入队列，继续寻找增广路，x染成黑色。

若v已经访问过，找到环
v为白色，是一个偶环，跳过。
v为黑色且u,v所在的奇环已经缩过了，那么也跳过。

否则，v为黑色，找到一个新的奇环，那么找到u,v所在奇环的环顶（即它们在BFS上跑出来的交错树的lca，称之为最近公共花祖先），将u到环顶的路径以及v到环顶的路径修改掉，白点染成黑点，加入队列，并将环上的点（或者是某个已经缩了的环顶）并查集父亲指向lca。

接下来就是代码部分，我们可以结合代码来理解上面的过程。

Code (UOJ #079)

#include 
#define fo(i,a,b) for(int i=a;i<=b;++i)
#define fod(i,a,b) for(int i=a;i>=b;--i)
#define N 505
#define M 130005
using namespace std;
int n,m,m1,fs[N],nt[2*M],dt[2*M],pre[N],match[N],f[N],bz[N],bp[N],ti,d[N*N];
void link(int x,int y)
{
	nt[++m1]=fs[x];
	dt[fs[x]=m1]=y;
}
int getf(int k)
{
	return (f[k]==k)?k:f[k]=getf(f[k]);
}
int lca(int x,int y)//整个lca实现比较巧妙，由于是BFS，那么这两个点在当前奇环上的深度一定相等，交替暴力寻找lca即可。
{
	ti++;x=getf(x),y=getf(y);
	while(bp[x]!=ti)
	{
		bp[x]=ti;//此处仅仅是一个标记，无其他作用
		x=getf(pre[match[x]]);
		if(y) swap(x,y);
	}
	return x;
}
void make(int x,int y,int w)//缩环（开花）过程
{
	while(getf(x)!=w)
	{
		pre[x]=y,y=match[x];//x是原本的黑点，y是原本的白点，将原本的pre边变成双向。
		if(bz[y]==2) bz[y]=1,d[++d[0]]=y;//若y还是白点则染黑
		if(getf(x)==x) f[x]=w;
		if(getf(y)==y) f[y]=w;
		x=pre[y];
	}
}
bool find(int st)//主过程
{
	fo(i,1,n) f[i]=i,pre[i]=bz[i]=0;
	d[d[0]=1]=st,bz[st]=1;
	int l=0;
	while(l<d[0])
	{
		int k=d[++l];
		for(int i=fs[k];i;i=nt[i])
		{
			int p=dt[i];
			if(getf(p)==getf(k)||bz[p]==2) continue;//如果找到一个已经缩过的奇环或者偶环则跳过
			if(!bz[p])
			{
				bz[p]=2,pre[p]=k;
				if(!match[p])//找到增广路
				{
					for(int x=p,y;x;x=y) y=match[pre[x]],match[x]=pre[x],match[pre[x]]=x;//返回修改匹配
					return 1;
				}
				bz[match[p]]=1,d[++d[0]]=match[p];//否则将其匹配点加入队列
			}
			else 
			{
				int w=lca(k,p);
				make(k,p,w);
				make(p,k,w);//以上分别修改k到lca的路径以及p到lca的路径（环的两半）
			}
		}
	}
	return 0;
}
int main()
{
	cin>>n>>m;
	fo(i,1,m)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		link(x,y),link(y,x);
	}
	int ans=0;
	fo(i,1,n) 
		if(!match[i]) ans+=find(i);
	printf("%d\n",ans);
	fo(i,1,n) printf("%d ",match[i]);
}