数据科学 案例5 Logistic回归之构建初始信用评级和分类模型检验（代码）

8 逻辑回归

信用风险建模案例
数据说明：本数据是一份汽车贷款违约数据
#名称—中文含义
#application_id—申请者ID
#account_number—帐户号
#bad_ind—是否违约
#vehicle_year—汽车购买时间
#vehicle_make—汽车制造商
#bankruptcy_ind—曾经破产标识
#tot_derog—五年内信用不良事件数量(比如手机欠费消号)
#tot_tr—全部帐户数量
#age_oldest_tr—最久账号存续时间(月)
#tot_open_tr—在使用帐户数量
#tot_rev_tr—在使用可循环贷款帐户数量(比如信用卡)
#tot_rev_debt—在使用可循环贷款帐户余额(比如信用卡欠款)
#tot_rev_line—可循环贷款帐户限额(信用卡授权额度)
#rev_util—可循环贷款帐户使用比例(余额/限额)
#fico_score—FICO打分
#purch_price—汽车购买金额(元)
#msrp—建议售价
#down_pyt—分期付款的首次交款
#loan_term—贷款期限(月)
#loan_amt—贷款金额
#ltv—贷款金额/建议售价*100
#tot_income—月均收入(元)
#veh_mileage—行使历程(Mile)
#used_ind—是否二手车
#weight—样本权重

import os
import numpy as np
from scipy import stats
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt

?pd.read_csv

1、导入数据和数据清洗

表格中有两行列标签（需注意）

accepts = pd.read_csv(r'.\data\accepts.csv',header =1,encoding='gbk')
accepts2 = accepts.drop([5845,5846,11692]).dropna() ##
accepts2.head()

	application_id	account_number	bad_ind	vehicle_year	vehicle_make	bankruptcy_ind	tot_derog	tot_tr	age_oldest_tr	tot_open_tr	...	purch_price	msrp	down_pyt	loan_term	loan_amt	ltv	tot_income	veh_mileage	used_ind	weight
0	2314049	11613	1	1998	FORD	N	7	9	64	2	...	17200	17350	0	36	17200	99	6550	24000	1	1
1	63539	13449	0	2000	DAEWOO	N	0	21	240	11	...	19588.54	19788	683.54	60	19588.54	99	4666.67	22	0	4.75
3	8725187	15359	1	1997	FORD	N	3	10	35	5	...	12999	12100	3099	60	10800	118	1500	10000	1	1
4	4275127	15812	0	2000	TOYOTA	N	0	10	104	2	...	26328.04	22024	0	60	26328.04	122	4144	14	0	4.75
5	8712513	16979	0	2000	DODGE	Y	2	15	136	4	...	26272.72	26375	0	36	26272.72	100	5400	1	0	4.75

5 rows × 25 columns

#把字符数据转化为浮点型数据
accepts2['tot_rev_line'] = accepts2['tot_rev_line'].astype(float)
accepts2['tot_income'] = accepts2['tot_income'].astype(float)
accepts2['loan_amt'] = accepts2['loan_amt'].astype(float)
accepts2['tot_income'] = accepts2['tot_income'].astype(float)
accepts2['down_pyt'] = accepts2['down_pyt'].astype(float)
accepts2['loan_amt'] = accepts2['loan_amt'].astype(float)
accepts2['tot_rev_debt'] = accepts2['tot_rev_debt'].astype(float)

2、衍生变量:

#定义除法
def divMy(x,y):
    import numpy as np
    if x==np.nan or y==np.nan:
        return np.nan
    elif y==0:
        return -1
    else:
        return x/y
divMy(1,2)

0.5

##历史负债收入比:tot_rev_line/tot_income
accepts2["dti_hist"]=accepts2[["tot_rev_line","tot_income"]].apply(lambda x:divMy(x[0],x[1]),axis = 1)
##本次新增负债收入比:loan_amt/tot_income
accepts2["dti_mew"]=accepts2[["loan_amt","tot_income"]].apply(lambda x:divMy(x[0],x[1]),axis = 1)
##本次贷款首付比例:down_pyt/loan_amt
accepts2["fta"]=accepts2[["down_pyt","loan_amt"]].apply(lambda x:divMy(x[0],x[1]),axis = 1)
##新增债务比:loan_amt/tot_rev_debt
accepts2["nth"]=accepts2[["loan_amt","tot_rev_debt"]].apply(lambda x:divMy(x[0],x[1]),axis = 1)
##新增债务额度比:loan_amt/tot_rev_line
accepts2["nta"]=accepts2[["loan_amt","tot_rev_line"]].apply(lambda x:divMy(x[0],x[1]),axis = 1)

accepts2.head()

	application_id	account_number	bad_ind	vehicle_year	vehicle_make	bankruptcy_ind	tot_derog	tot_tr	age_oldest_tr	tot_open_tr	...	ltv	tot_income	veh_mileage	used_ind	weight	dti_hist	dti_mew	fta	nth	nta
0	2314049	11613	1	1998	FORD	N	7	9	64	2	...	99	6550.00	24000	1	1	0.076336	2.625954	0.000000	33.992095	34.400000
1	63539	13449	0	2000	DAEWOO	N	0	21	240	11	...	99	4666.67	22	0	4.75	12.265920	4.197541	0.034895	0.566061	0.342212
3	8725187	15359	1	1997	FORD	N	3	10	35	5	...	118	1500.00	10000	1	1	3.964000	7.200000	0.286944	2.687236	1.816347
4	4275127	15812	0	2000	TOYOTA	N	0	10	104	2	...	122	4144.00	14	0	4.75	0.434363	6.353292	0.000000	-1.000000	14.626689
5	8712513	16979	0	2000	DODGE	Y	2	15	136	4	...	100	5400.00	1	0	4.75	1.064259	4.865319	0.000000	7.196034	4.571554

5 rows × 30 columns

3、分类变量的相关关系

3.1 交叉表

cross_table = pd.crosstab(accepts2.used_ind,accepts2.bad_ind, margins=True)
#cross_table = pd.crosstab(accepts.bankruptcy_ind,accepts.bad_ind, margins=True)
cross_table

bad_ind	0	1	All
used_ind
0	2914	612	3526
1	3724	960	4684
All	6638	1572	8210

3.2 列联表

#法一：
def percConvert(ser):
    return ser/float(ser[-1])

cross_table = pd.crosstab(accepts2.used_ind,accepts2.bad_ind, margins=True)
cross_table.apply(percConvert, axis=1)

bad_ind	0	1	All
used_ind
0	0.826432	0.173568	1.0
1	0.795047	0.204953	1.0
All	0.808526	0.191474	1.0

print('''chisq = %6.4f 
p-value = %6.4f
dof = %i 
expected_freq = %s'''  %stats.chi2_contingency(cross_table.iloc[:2, :2]))

chisq = 12.5979 
p-value = 0.0004
dof = 1 
expected_freq = [[2850.86333739  675.13666261]
 [3787.13666261  896.86333739]]

#法二：(与预计的结果不一样,目前以方法一为准)
cross_table = pd.crosstab(accepts2.used_ind,accepts2.bad_ind, margins=False)
cross_table = cross_table.div(cross_table.sum(1),axis = 0)
cross_table

print('''chisq = %6.4f 
p-value = %6.4f
dof = %i 
expected_freq = %s'''  %stats.chi2_contingency(cross_table.iloc[:2, :2]))

4、线性回归

4.1 数据预处理（字符型转化为数值型，查看变量间的关系）

# 中文乱码的处理
plt.rcParams['font.sans-serif'] = [u'SimHei']
plt.rcParams['axes.unicode_minus'] = False
#导入进来的数据为字符串，先将其转化为数值型
accepts2['age_oldest_tr'] = accepts2['age_oldest_tr'].astype(int)
accepts2['bad_ind'] = accepts2['bad_ind'].astype(int)

accepts2.plot(x = 'age_oldest_tr',y = 'bad_ind', kind = 'scatter')
# plt.scatter(x=accepts2.age_oldest_tr, y=accepts2.bad_ind)

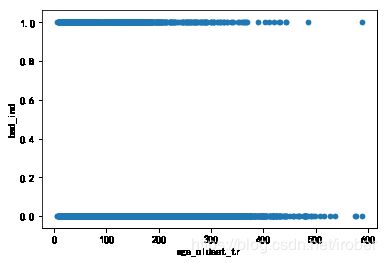
4.2 随机抽样，建立训练集与测试集

#为5.2 1向前法预处理
candidates = ['bad_ind','tot_derog','age_oldest_tr','tot_open_tr','rev_util','fico_score','loan_term','ltv',
              'veh_mileage','dti_hist','dti_mew','fta','nth','nta']
accepts2[candidates] = accepts2[candidates].astype(float)

train = accepts2.sample(frac=0.7, random_state=1234).copy()
test = accepts2[~ accepts2.index.isin(train.index)].copy()
print(' 训练集样本量: %i \n 测试集样本量: %i' %(len(train), len(test)))

 训练集样本量: 5747 
 测试集样本量: 2463

4.3 线性回归

lg = smf.glm('bad_ind ~ age_oldest_tr', data=train, 
             family=sm.families.Binomial(sm.families.links.logit)).fit()  #逻辑回归，0-1分布（伯努利分布）
lg.summary()

Generalized Linear Model Regression Results

Dep. Variable:	bad_ind	No. Observations:	5747
Model:	GLM	Df Residuals:	5745
Model Family:	Binomial	Df Model:	1
Link Function:	logit	Scale:	1.0000
Method:	IRLS	Log-Likelihood:	-2730.8
Date:	Sat, 15 Feb 2020	Deviance:	5461.6
Time:	11:24:04	Pearson chi2:	5.89e+03
No. Iterations:	5	Covariance Type:	nonrobust

	coef	std err	z	P>|z|	[0.025	0.975]
Intercept	-0.5769	0.065	-8.897	0.000	-0.704	-0.450
age_oldest_tr	-0.0057	0.000	-13.682	0.000	-0.006	-0.005

4.4 预测

train['proba'] = lg.predict(train)
test['proba'] = lg.predict(test)

test['proba'].head(10)

4     0.237216
10    0.155657
13    0.277338
20    0.060517
22    0.235165
25    0.098014
27    0.050966
32    0.193184
51    0.254062
52    0.318912
Name: proba, dtype: float64

4.5 模型评估

1、设定阈值

# 设定阈值

test['prediction'] = (test['proba'] > 0.3).astype('int')

2、混淆矩阵

pd.crosstab(test.bad_ind, test.prediction, margins=True)

prediction	0	1	All
bad_ind
0.0	1877	138	2015
1.0	366	82	448
All	2243	220	2463

3、计算准确率

acc = sum(test['prediction'] == test['bad_ind']) /np.float(len(test))
print('The accurancy is %.2f' %acc)

The accurancy is 0.80

#选取准确率最高的阈值
for i in np.arange(0.02, 0.3, 0.02):
    prediction = (test['proba'] > i).astype('int')
    confusion_matrix = pd.crosstab(prediction,test.bad_ind,
                                   margins = True)
    precision = confusion_matrix.loc[0, 0] /confusion_matrix.loc['All', 0]
    recall = confusion_matrix.loc[0, 0] / confusion_matrix.loc[0, 'All']
    Specificity = confusion_matrix.loc[1, 1] /confusion_matrix.loc[1,'All']
    f1_score = 2 * (precision * recall) / (precision + recall)
    print('threshold: %s, precision: %.2f, recall:%.2f ,Specificity:%.2f , f1_score:%.2f'%(i, precision, recall, Specificity,f1_score))

threshold: 0.02, precision: 0.00, recall:0.50 ,Specificity:0.18 , f1_score:0.00
threshold: 0.04, precision: 0.01, recall:0.94 ,Specificity:0.18 , f1_score:0.02
threshold: 0.06, precision: 0.03, recall:0.92 ,Specificity:0.18 , f1_score:0.06
threshold: 0.08, precision: 0.07, recall:0.93 ,Specificity:0.19 , f1_score:0.14
threshold: 0.1, precision: 0.13, recall:0.92 ,Specificity:0.19 , f1_score:0.23
threshold: 0.12000000000000001, precision: 0.21, recall:0.92 ,Specificity:0.21 , f1_score:0.34
threshold: 0.13999999999999999, precision: 0.27, recall:0.92 ,Specificity:0.21 , f1_score:0.42
threshold: 0.16, precision: 0.35, recall:0.90 ,Specificity:0.22 , f1_score:0.51
threshold: 0.18, precision: 0.44, recall:0.89 ,Specificity:0.23 , f1_score:0.59
threshold: 0.19999999999999998, precision: 0.56, recall:0.87 ,Specificity:0.24 , f1_score:0.68
threshold: 0.22, precision: 0.68, recall:0.87 ,Specificity:0.27 , f1_score:0.77
threshold: 0.24, precision: 0.76, recall:0.85 ,Specificity:0.28 , f1_score:0.81
threshold: 0.26, precision: 0.83, recall:0.85 ,Specificity:0.32 , f1_score:0.84
threshold: 0.28, precision: 0.88, recall:0.85 ,Specificity:0.34 , f1_score:0.86

4、绘制ROC曲线

import sklearn.metrics as metrics

fpr_test, tpr_test, th_test = metrics.roc_curve(test.bad_ind, test.proba)
fpr_train, tpr_train, th_train = metrics.roc_curve(train.bad_ind, train.proba)

plt.figure(figsize=[3, 3])
plt.plot(fpr_test, tpr_test, 'b--')
plt.plot(fpr_train, tpr_train, 'r-')
plt.title('ROC curve')
plt.show()
print('AUC = %.4f' %metrics.auc(fpr_test, tpr_test))

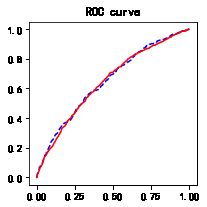
AUC = 0.6488

5、逻辑回归

5.1 包含分类预测变量的逻辑回归

formula = '''bad_ind ~ C(used_ind)'''

lg_m = smf.glm(formula=formula, data=train, 
             family=sm.families.Binomial(sm.families.links.logit)).fit()
lg_m.summary()

Generalized Linear Model Regression Results

Dep. Variable:	bad_ind	No. Observations:	5747
Model:	GLM	Df Residuals:	5745
Model Family:	Binomial	Df Model:	1
Link Function:	logit	Scale:	1.0000
Method:	IRLS	Log-Likelihood:	-2836.2
Date:	Sat, 15 Feb 2020	Deviance:	5672.4
Time:	11:24:31	Pearson chi2:	5.75e+03
No. Iterations:	4	Covariance Type:	nonrobust

	coef	std err	z	P>|z|	[0.025	0.975]
Intercept	-1.5267	0.053	-29.060	0.000	-1.630	-1.424
C(used_ind)[T.1]	0.1927	0.068	2.838	0.005	0.060	0.326

5.2 多元逻辑回归

1、向前法

def forward_select(data, response):
    remaining = set(data.columns)
    remaining.remove(response)
    selected = []
    current_score, best_new_score = float('inf'), float('inf')
    while remaining:
        aic_with_candidates=[]
        for candidate in remaining:
            formula = "{} ~ {}".format(
                response,' + '.join(selected + [candidate]))
            aic = smf.glm(
                formula=formula, data=data, 
                family=sm.families.Binomial(sm.families.links.logit)
            ).fit().aic
            aic_with_candidates.append((aic, candidate))
        aic_with_candidates.sort(reverse=True)
        best_new_score, best_candidate=aic_with_candidates.pop()
        if current_score > best_new_score: 
            remaining.remove(best_candidate)
            selected.append(best_candidate)
            current_score = best_new_score
            print ('aic is {},continuing!'.format(current_score))
        else:        
            print ('forward selection over!')
            break
            
    formula = "{} ~ {} ".format(response,' + '.join(selected))
    print('final formula is {}'.format(formula))
    model = smf.glm(
        formula=formula, data=data, 
        family=sm.families.Binomial(sm.families.links.logit)
    ).fit()
    return(model)

#只有连续变量可以进行变量筛选，分类变量需要进行WOE转换才可以进行变量筛选
candidates = ['bad_ind','tot_derog','age_oldest_tr','tot_open_tr','rev_util','fico_score','loan_term','ltv',
              'veh_mileage','dti_hist','dti_mew','fta','nth','nta']
data_for_select = train[candidates]

lg_m1 = forward_select(data=data_for_select, response='bad_ind')
lg_m1.summary()

aic is 5112.102444955438,continuing!
aic is 4930.620746960663,continuing!
aic is 4867.936361578135,continuing!
aic is 4862.177989178937,continuing!
aic is 4856.0240437714365,continuing!
aic is 4853.140577715231,continuing!
aic is 4851.285414957676,continuing!
forward selection over!
final formula is bad_ind ~ fico_score + ltv + age_oldest_tr + rev_util + nth + tot_derog + fta 

Generalized Linear Model Regression Results

Dep. Variable:	bad_ind	No. Observations:	5747
Model:	GLM	Df Residuals:	5739
Model Family:	Binomial	Df Model:	7
Link Function:	logit	Scale:	1.0000
Method:	IRLS	Log-Likelihood:	-2417.6
Date:	Sat, 15 Feb 2020	Deviance:	4835.3
Time:	11:24:47	Pearson chi2:	5.60e+03
No. Iterations:	6	Covariance Type:	nonrobust

	coef	std err	z	P>|z|	[0.025	0.975]
Intercept	5.6094	0.591	9.491	0.000	4.451	6.768
fico_score	-0.0139	0.001	-16.606	0.000	-0.015	-0.012
ltv	0.0278	0.002	11.201	0.000	0.023	0.033
age_oldest_tr	-0.0035	0.000	-7.929	0.000	-0.004	-0.003
rev_util	0.0010	0.000	2.564	0.010	0.000	0.002
nth	0.0004	0.000	2.529	0.011	8.63e-05	0.001
tot_derog	0.0253	0.011	2.271	0.023	0.003	0.047
fta	-0.6570	0.349	-1.880	0.060	-1.342	0.028

2、计算方差膨胀因子

# Seemingly wrong when using 'statsmmodels.stats.outliers_influence.variance_inflation_factor'
#计算方差膨胀因子，若其> 10 表示某变量的多重共线性严重.
def vif(df, col_i):
    from statsmodels.formula.api import ols
    
    cols = list(df.columns)
    cols.remove(col_i)
    cols_noti = cols
    formula = col_i + '~' + '+'.join(cols_noti)
    r2 = ols(formula, df).fit().rsquared
    return 1. / (1. - r2)

candidates = ['bad_ind','fico_score','ltv','age_oldest_tr','tot_derog','nth','tot_open_tr','veh_mileage','rev_util']
exog = train[candidates].drop(['bad_ind'], axis=1)

for i in exog.columns:
    print(i, '\t', vif(df=exog, col_i=i))

fico_score 	 1.6474312909303999
ltv 	 1.0312076990808654
age_oldest_tr 	 1.2398180183116478
tot_derog 	 1.387916859405689
nth 	 1.019005900596472
tot_open_tr 	 1.130385791173031
veh_mileage 	 1.0249442971334133
rev_util 	 1.0857772491871416

train['proba'] = lg_m1.predict(train)
test['proba'] = lg_m1.predict(test)
#ROC曲线
import sklearn.metrics as metrics

fpr_test, tpr_test, th_test = metrics.roc_curve(test.bad_ind, test.proba)
fpr_train, tpr_train, th_train = metrics.roc_curve(train.bad_ind, train.proba)

plt.figure(figsize=[3, 3])
plt.plot(fpr_test, tpr_test, 'b--')
plt.plot(fpr_train, tpr_train, 'r-')
plt.title('ROC curve')
plt.show()

print('AUC = %.4f' %metrics.auc(fpr_test, tpr_test))

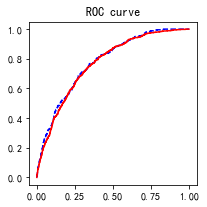
AUC = 0.7756

6、其他变量处理

目前vehicle_year、vehicle_make、bankruptcy_ind、used_ind这些分类变量无法通过逐步变量筛选法

解决方案：

• 1、逐一根据显著性测试
• 2、使用决策树等方法筛选变量，但是多分类变量需要事先进行变量概化
• 3、使用WOE转换，多分类变量也需要事先进行概化，使用scorecardpy包中的woe算法可以自动进行概化

使用第一种方法

#formula = '''bad_ind ~ fico_score+ltv+age_oldest_tr+tot_derog+nth+tot_open_tr+veh_mileage+rev_util+C(used_ind)+C(vehicle_year)+C(bankruptcy_ind)'''
formula = '''bad_ind ~ fico_score+ltv+age_oldest_tr+tot_derog+nth+tot_open_tr+veh_mileage+rev_util+C(bankruptcy_ind)'''
lg_m = smf.glm(formula=formula, data=train, 
             family=sm.families.Binomial(sm.families.links.logit)).fit()
lg_m.summary()

Generalized Linear Model Regression Results

Dep. Variable:	bad_ind	No. Observations:	5747
Model:	GLM	Df Residuals:	5737
Model Family:	Binomial	Df Model:	9
Link Function:	logit	Scale:	1.0000
Method:	IRLS	Log-Likelihood:	-2416.0
Date:	Sat, 15 Feb 2020	Deviance:	4832.0
Time:	11:44:38	Pearson chi2:	5.54e+03
No. Iterations:	6	Covariance Type:	nonrobust

	coef	std err	z	P>|z|	[0.025	0.975]
Intercept	5.4394	0.596	9.122	0.000	4.271	6.608
C(bankruptcy_ind)[T.Y]	-0.3261	0.136	-2.397	0.017	-0.593	-0.059
fico_score	-0.0138	0.001	-16.393	0.000	-0.015	-0.012
ltv	0.0290	0.002	12.024	0.000	0.024	0.034
age_oldest_tr	-0.0034	0.000	-7.282	0.000	-0.004	-0.002
tot_derog	0.0330	0.012	2.788	0.005	0.010	0.056
nth	0.0004	0.000	2.617	0.009	9.82e-05	0.001
tot_open_tr	-0.0103	0.012	-0.866	0.387	-0.034	0.013
veh_mileage	8.365e-07	1.17e-06	0.713	0.476	-1.46e-06	3.14e-06
rev_util	0.0011	0.000	2.610	0.009	0.000	0.002