转载：奇异值分解(SVD)原理详解及推导

   转载出处http://blog.csdn.net/zhongkejingwang/article/details/43053513

       网上关于矩阵和映射之间的对应关系的文章较少。A Singularly Valuable Decomposition The SVD of a Matrix，把矩阵和空间关系对应了起来。本文就参考了该文并结合矩阵的相关知识把SVD原理梳理一下。

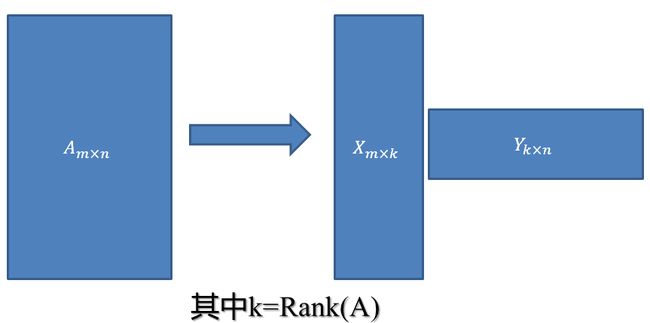
   SVD不仅是一个数学问题，在工程应用中的很多地方都有它的身影，比如PCA，掌握了SVD原理后再去看PCA那是相当简单的，在推荐系统方面，SVD更是名声大噪，将它应用于推荐系统的是Netflix大奖的获得者Koren，可以在Google上找到他写的文章；用SVD可以很容易得到任意矩阵的满秩分解，用满秩分解可以对数据做压缩。可以用SVD来证明对任意M*N的矩阵均存在如下分解：

这个可以应用在数据降维压缩上！在数据相关性特别大的情况下存储X和Y矩阵比存储A矩阵占用空间更小！

   在开始讲解SVD之前，先补充一点矩阵代数的相关知识。

正交矩阵

   正交矩阵是在欧几里得空间里的叫法，在酉空间里叫酉矩阵，一个正交矩阵对应的变换叫正交变换，这个变换的特点是不改变向量的尺寸和向量间的夹角，那么它到底是个什么样的变换呢？看下面这张图

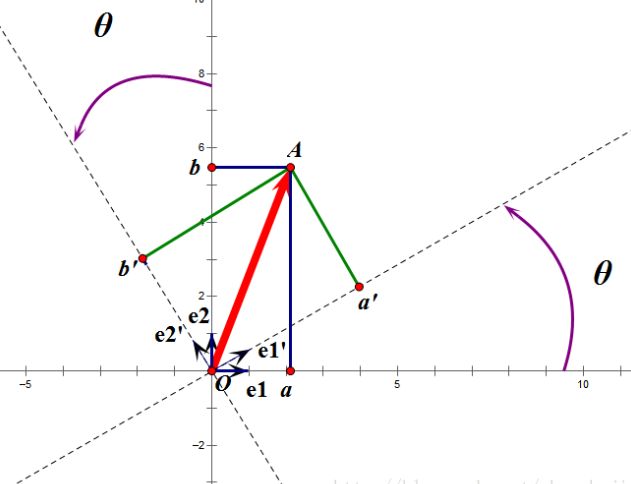
假设二维空间中的一个向量OA，它在标准坐标系也即e1、e2表示的坐标是中表示为(a,b)’（用’表示转置）。现在把它用另一组坐标e1’、e2’表示为(a’,b’)’，存在矩阵U使得(a’,b’)’=U(a,b)’，则U即为正交矩阵。从图中可以看到，正交变换只是将变换向量用另一组正交基表示，在这个过程中并没有对向量做拉伸，也不改变向量的空间位置。若对两个向量同时做正交变换，那么变换前后这两个向量的夹角显然不会改变。上面的例子只是正交变换的一个方面，即旋转变换，可以把e1’、e2’坐标系看做是e1、e2坐标系经过旋转某个$\theta$得到，怎么样得到该旋转矩阵U呢？如下
$$x=\left[\begin{array}{c}a\\ b\end{array}\right]$$$$\begin{array}{l}{a}^{\prime }=x\cdot e{1}^{\prime }=e{1}^{{\prime }^T}x\\ b^{\prime }=x\cdot e{2}^{\prime }=e{2}^{{\prime }^T}x\end{array}$$

a'和b'实际上是x在e1'和e2'轴上的投影大小，所以直接做内积可得:

$$\left[\begin{array}{c}{a}^{\prime }\\ b^{\prime }\end{array}\right]=\left[\begin{array}{c}e{1}^{{\prime }^T}\\ e{2}^{{\prime }^T}\end{array}\right]x$$

从图中可以看到

$$e{1}^{\prime }=\left[\begin{array}{c}cos\theta \\ sin\theta \end{array}\right],e{2}^{\prime }=\left[\begin{array}{c}-sin\theta \\ cos\theta \end{array}\right]$$

所以

$$\text{U}=\left[\begin{array}{cc}cos\theta & sin\theta \\ -sin\theta & cos\theta \end{array}\right]$$

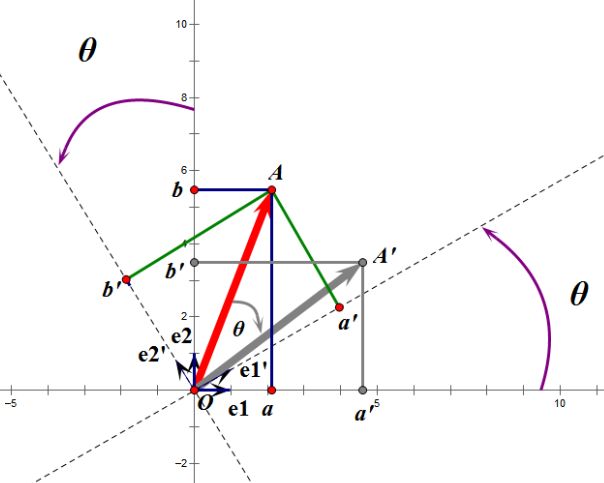
正交阵U行（列）向量之间都是单位正交向量。上面求得的是一个旋转矩阵，它对向量做旋转变换！也许你会有疑问：刚才不是说向量空间位置不变吗？怎么现在又说它被旋转了？对的，这两个并没有冲突，说空间位置不变是绝对的，但是坐标是相对的，加入你站在e1上看OA，随着e1旋转到e1'，看OA的位置就会改变。如下图：

如图，如果我选择了e1'、e2'作为新的标准坐标系，那么在新坐标系中OA（原标准坐标系的表示）就变成了OA'，这样看来就好像坐标系不动，把OA往顺时针方向旋转了“斯塔”角度，这个操作实现起来很简单：将变换后的向量坐标仍然表示在当前坐标系中。

旋转变换是正交变换的一个方面，这个挺有用的，比如在开发中需要实现某种旋转效果，直接可以用旋转变换实现。正交变换的另一个方面是反射变换，也即e1'的方向与图中方向相反，这个不再讨论。

总结：正交矩阵的行（列）向量都是两两正交的单位向量，正交矩阵对应的变换为正交变换，它有两种表现：旋转和反射。正交矩阵将标准正交基映射为标准正交基（即图中从e1、e2到e1'、e2'）

特征值分解——EVD

    在讨论SVD之前先讨论矩阵的特征值分解（EVD），在这里，选择一种特殊的矩阵——对称阵（酉空间中叫hermite矩阵即厄米阵）。对称阵有一个很优美的性质：它总能相似对角化，对称阵不同特征值对应的特征向量两两正交。一个矩阵能相似对角化即说明其特征子空间即为其列空间，若不能对角化则其特征子空间为列空间的子空间。现在假设存在mxm的满秩对称矩阵A，它有m个不同的特征值，设特征值为:

$${\lambda }_i$$

对应的单位特征向量为

$$x_i$$

则有

$$\begin{array}{rl}A{x}_1& ={\lambda }_1{x}_1\\ A{x}_2& ={\lambda }_2{x}_2\\ & \dots \\ A{x}_m& ={\lambda }_m{x}_m\end{array}$$

进而

$$\mathbf{A}\mathbf{U}=\mathbf{U}\mathbf{\Lambda }$$$$\mathbf{U}=\left[\begin{array}{cccc}{x}_1\text{x1}{x}_1& x_2\text{x2}{x}_2& \cdots & x_m\text{xm}{x}_m\end{array}\right]$$

$$\mathbf{\Lambda }=\left[\begin{array}{ccc}{\lambda }_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\lambda }_m\end{array}\right]$$

所以可得到A的特征值分解（由于对称阵特征向量两两正交，所以U为正交阵，正交阵的逆矩阵等于其转置）

$$\mathbf{A}=\mathbf{U}\mathbf{\Lambda }{\mathbf{U}}^{-1}=\mathbf{U}\mathbf{\Lambda }{\mathbf{U}}^{\mathbf{T}}$$

这里假设A有m个不同的特征值，实际上，只要A是对称阵其均有如上分解。

矩阵A分解了，相应的，其对应的映射也分解为三个映射。现在假设有x向量，用Ａ将其变换到Ａ的列空间中，那么首先由U'先对x做变换：

$$\mathbf{A}\mathbf{x}=\mathbf{U}\mathbf{\Lambda }{\mathbf{U}}^{\mathbf{T}}\mathbf{x}$$

U是正交阵U'也是正交阵，所以U'对x的变换是正交变换，它将x用新的坐标系来表示，这个坐标系就是A的所有正交的特征向量构成的坐标系。比如将x用A的所有特征向量表示为：(这里把箭头形式的向量用粗体表示)

$$x\text{x}x=a_1{x}_1\text{x1}{x}_1+a_2{x}_2\text{x2}{x}_2+\cdots +a_m{x}_m\text{xm}{x}_m$$

则通过第一个变换就可以把x表示为[a1 a2 ... am]'：(a1、a2等是标量)

$$\mathbf{U}\mathbf{\Lambda }{\mathbf{U}}^{\mathbf{T}}\mathbf{x}=\mathbf{U}\mathbf{\Lambda }\left[\begin{array}{c}{x}_1^T\text{x1T}{x}_1^T\\ x_2^T\text{x2T}{x}_2^T\\ ⋮\\ x_m^T\text{xmT}{x}_m^T\end{array}\right]\left(a_1{x}_1\text{x1}{x}_1+a_2{x}_2\text{x2}{x}_2+\cdots +a_m{x}_m\text{xm}{x}_m\right)=U\text{U}U\Lambda \text{Λ}\Lambda \left[\begin{array}{c}{a}_1\\ a_2\\ ⋮\\ a_m\end{array}\right]$$

紧接着，在新的坐标系表示下，由中间那个对角矩阵对新的向量坐标换，其结果就是将向量往各个轴方向拉伸或压缩：

$$\mathbf{U}\mathbf{\Lambda }\left[\begin{array}{c}{a}_1\\ a_2\\ ⋮\\ a_m\end{array}\right]=\mathbf{U}\left[\begin{array}{ccc}{\lambda }_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\lambda }_m\end{array}\right]\left[\begin{array}{c}{a}_1\\ a_2\\ ⋮\\ a_m\end{array}\right]=\mathbf{U}\left[\begin{array}{c}{\lambda }_1{a}_1\\ {\lambda }_2{a}_2\\ ⋮\\ {\lambda }_m{a}_m\end{array}\right]$$

从上图可以看到，如果A不是满秩的话，那么就是说对角阵的对角线上元素存在0，这时候就会导致维度退化，这样就会使映射后的向量落入m维空间的子空间中。

最后一个变换就是U对拉伸或压缩后的向量做变换，由于U和U'是互为逆矩阵，所以U变换是U'变换的逆变换。

因此，从对称阵的分解对应的映射分解来分析一个矩阵的变换特点是非常直观的。假设对称阵特征值全为1那么显然它就是单位阵，如果对称阵的特征值有个别是0其他全是1，那么它就是一个正交投影矩阵，它将m维向量投影到它的列空间中。

根据对称阵A的特征向量，如果A是2*2的，那么就可以在二维平面中找到这样一个矩形，是的这个矩形经过A变换后还是矩形：

                                      

这个矩形的选择就是让其边都落在A的特征向量方向上，如果选择其他矩形的话变换后的图形就不是矩形了！

奇异值分解——SVD

   上面的特征值分解的A矩阵是对称阵，根据EVD可以找到一个（超）矩形使得变换后还是（超）矩形，也即A可以将一组正交基映射到另一组正交基！那么现在来分析：对任意M*N的矩阵，能否找到一组正交基使得经过它变换后还是正交基？答案是肯定的，它就是SVD分解的精髓所在。

   现在假设存在M*N矩阵A，事实上，A矩阵将n维空间中的向量映射到k（k<=m）维空间中，k=Rank(A)。现在的目标就是：在n维空间中找一组正交基，使得经过A变换后还是正交的。假设已经找到这样一组正交基：

$$\left\{{\mathbf{v}}_1,{\mathbf{v}}_2,\dots ,{\mathbf{v}}_{\mathbf{n}}\right\}$$

则A矩阵将这组基映射为：

$$\left\{\mathbf{A}{\mathbf{v}}_1,\mathbf{A}{\mathbf{v}}_2,\dots ,\mathbf{A}{\mathbf{v}}_{\mathbf{n}}\right\}$$

如果要使他们两两正交，即

$$\mathrm{A}{\mathbf{v}}_{\mathbf{i}}\cdot \mathbf{A}{\mathbf{v}}_{\mathbf{j}}={\left(\mathrm{A}{\mathbf{v}}_{\mathbf{i}}\right)}^{\mathbf{T}}\mathbf{A}{\mathbf{v}}_{\mathbf{j}}={\mathbf{v}}_{\mathbf{i}}^{\mathbf{T}}{\mathbf{A}}^{\mathbf{T}}\mathrm{A}{\mathbf{v}}_{\mathbf{j}}=0$$

根据假设，存在

$${\mathbf{v}}_{\mathbf{i}}^{\mathbf{T}}{\mathbf{v}}_{\mathbf{j}}={\mathbf{v}}_{\mathbf{i}}\cdot {\mathbf{v}}_{\mathbf{j}}=0$$

所以如果正交基v选择为A'A的特征向量的话，由于A'A是对称阵，v之间两两正交，那么

$${\mathbf{v}}_{\mathbf{i}}^{\mathbf{T}}{\mathbf{A}}^{\mathbf{T}}\mathbf{A}{\mathbf{v}}_{\mathbf{j}}={\mathbf{v}}_{\mathbf{i}}^{\mathbf{T}}{\lambda }_j{v}_j\text{vj}{v}_j={\lambda }_j{v}_i^T\text{viT}{v}_i^T{v}_j\text{vj}{v}_j={\lambda }_j{v}_i\text{vi}{v}_i\cdot v_j\text{vj}{v}_j=0$$

这样就找到了正交基使其映射后还是正交基了，现在，将映射后的正交基单位化：

因为

$$\mathbf{A}{\mathbf{v}}_{\mathbf{i}}\cdot \mathbf{A}{\mathbf{v}}_{\mathbf{i}}={\lambda }_i{v}_i\text{vi}{v}_i\cdot v_i\text{vi}{v}_i={\lambda }_i$$

所以有

$${\left|\mathbf{A}{\mathbf{v}}_{\mathbf{i}}\right|}^2={\lambda }_i\ge 0$$

所以取单位向量

$${\mathbf{u}}_{\mathbf{i}}=\frac{\mathbf{A}{\mathbf{v}}_{\mathbf{i}}}{\left|\mathbf{A}{\mathbf{v}}_{\mathbf{i}}\right|}=\frac{1}{\sqrt{{\lambda }_i}}\mathbf{A}{\mathbf{v}}_{\mathbf{i}}$$

由此可得

                

当k < i <= m时，对u1，u2，...，uk进行扩展u(k+1),...,um，使得u1，u2，...，um为m维空间中的一组正交基，即

同样的，对v1，v2，...，vk进行扩展v(k+1),...,vn（这n-k个向量存在于A的零空间中，即Ax=0的解空间的基），使得v1，v2，...，vn为n维空间中的一组正交基，即

则可得到

继而可以得到A矩阵的奇异值分解：

                                                 

                

现在可以来对A矩阵的映射过程进行分析了：如果在n维空间中找到一个（超）矩形，其边都落在A'A的特征向量的方向上，那么经过A变换后的形状仍然为（超）矩形！

vi为A'A的特征向量，称为A的右奇异向量，ui=Avi实际上为AA'的特征向量，称为A的左奇异向量。下面利用SVD证明文章一开始的满秩分解：

利用矩阵分块乘法展开得：

可以看到第二项为0，有

                               

令

           

则A=XY即是A的满秩分解。

整个SVD的推导过程就是这样，后面会介绍SVD在推荐系统中的具体应用，也就是复现Koren论文中的算法以及其推导过程。

参考文献：A Singularly Valuable Decomposition The SVD of a Matrix