对超长整数运算(大数运算)的算法探究
对超长整数运算(大数运算)的算法探究
至繁归于至简,这次自己仍然用尽可能易理解和阅读的解决方式。
前言:
刚有空闲,把以前自己写的大数相乘:http://blog.csdn.net/sunkun2013/article/details/11822927和大数相除:http://blog.csdn.net/sunkun2013/article/details/11833515运算的博客看了下,发现有一些不足,特别是冗余问题以及思想不够精简,与我坚信的“至繁归于至简”理念相冲突。既然今晚有时间,那我就把大数运算的算法自己再探究一番吧。
1、问题说明:
基于记忆体的有效运用,程式语言中规定了各种不同的资料型态,也因此变数所可以表达的最大整数受到限制,例如123456789123456789这样的整数就不可能储存在long变数中(例如C/C++等),我们称这为long数,这边翻为超长整数(避免与资料型态的长整数翻译混淆),或俗称大数运算。(此段为百度得到,)
2、解法:
既然一个变数无法表示超长整数,那么我们使用多个变数好了。当然这使用阵列最为方便,假设程式语言的最大资料型态可以储存至65535的数好了,为了计算方便及符合使用十进位制的习惯,让每一个阵列元素可以储存四个位数,也就是0到9999的数,例如:
很多人可能问到如何计算像50!这样的问题,解法就是使用程式中的乘法函式,至于要算到多大,就看需求了。
由于使用阵列来储存数值,关于数值在运算时的加减乘除等各种运算、位数的进位或借位就必须自行定义,加、减、乘都是由低位数开始运算,而除法则是由高位数开始运算,下边直接给出相应的具体代码,以下的N为阵列长度。
3、具体代码:
/**
* @Title 对超长整数运算(大数运算)的算法探究
* @Author 孙琨
* @Date 2013-11-18
* @At XUST
* @All Copyright by 孙琨
*
*/
#include
using namespace std;
#define N 1000
void add(int *a,int *b,int *c); // 大数相加, a:被加数,b:加数,c:运算结果
void sub(int *a,int *b,int *c); // 大数相减, a:被减数,b:减数,c:运算结果
void mul(int *a,int b,int *c); // 大数相乘, a:被乘数,b:乘数,c:运算结果
void div(int *a,int b,int *c); // 大数相除, a:被除数,b:除数,c:运算结果
void result(int *c); // 输出运算结果
int main(void)
{
int a1[N] = {3345,1458,3423,2345};
int b1[N] = {1234,5678,2234,5678};
int c1[N];
cout << "①大数相加运算" << endl;
cout << " 3345145834232345" << endl;
cout << "+" ;
cout << " 1234567822345678" << endl;
cout << "--------------------" << endl;
cout << "= " ;
add(a1,b1,c1);
result(c1);
cout << endl;
cout << "②大数相减运算" << endl;
cout << " 3345145834232345" << endl;
cout << "-" ;
cout << " 1234567822345678" << endl;
cout << "--------------------" << endl;
cout << "= " ;
sub(a1,b1,c1);
result(c1);
cout << endl;
int a2[N] = {1234,5678,2234,5678};
int b2 = {3};
int c2[N];
cout << "③大数相乘运算" << endl;
cout << " 1234567822345678" << endl;
cout << "×" ;
cout << " 3" << endl;
cout << "--------------------" << endl;
cout << "= " ;
mul(a2,b2,c2);
result(c2);
cout << endl;
cout << "④大数相除运算" << endl;
cout << " 1234567822345678" << endl;
cout << "÷" ;
cout << " 3" << endl;
cout << "--------------------" << endl;
cout << "= " ;
div(a2,b2,c2);
result(c2);
return 0;
}
void add(int *a,int *b,int *c)
{
int i,carry = 0;
for(i=N-1; i>=0; i--)
{
c[i] = a[i] + b[i] + carry;
if(c[i]<10000)
carry = 0;
else // 进位
{
c[i] = c[i] - 10000;
carry = 1;
}
}
}
void sub(int *a,int *b,int *c)
{
int i,borrow = 0;
for(i=N-1; i>=0; i--)
{
c[i] = a[i] - b[i] - borrow;
if(c[i] >= 0)
borrow = 0;
else // 借位
{
c[i] = c[i] + 10000;
borrow = 1;
}
}
}
void mul(int *a,int b,int *c) // b为乘数
{
int i,temp,carry = 0;
for(i=N-1; i>=0; i--)
{
temp = a[i] * b + carry;
c[i] = temp % 10000;
carry = temp / 10000;
}
}
void div(int *a,int b,int *c) // b为除数
{
int i,temp,remain = 0;
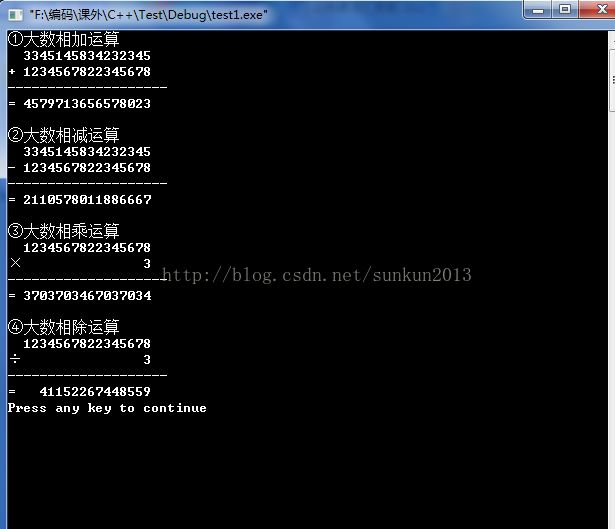
for(i=0; i 4、运行结果截图
5、备注:
上述代码主要目的是对算法进行了相应的阐述,在实际应用时,还应对上述代码进行修改,比如要考虑大数运算结果的正负号问题,以及运算结果的取长度问题等等