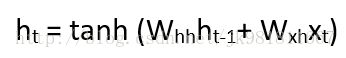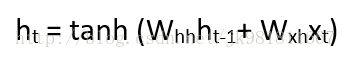一步一步分析讲解深度神经网络基础-Recurrent Neural Networks

我们知道在现实生活中，我们的数据往往和时间相关。 Time-Series Data就是说时间序列数据。
我们身体里的基因也是一种序列。
the data of a genome sequence- where every sequence has a different meaning.
基因组序列的数据，其中每个序列具有不同的含义。
而RNNs是处理Time-Series Data最新的一系列的人工神经网络技术。今天，我们来入门最简单的RNN模型。

1，RNNs能做什么？

在深入研究循环神经网络的细节之前，让我们思考一下，如果我们确实需要一个专门用于处理信息序列的网络。 还有什么样的任务能够用到这样的网络？

循环神经网络的优点在于其应用的多样性。 当我们处理RNN时，他们有很强的处理各种输入和输出类型的能力。

• Sentiment Classification - 这可以是简单地将tweets 分为积极和消极情绪的任务。
  所以这里的输入是一个不同长度的推文，而输出是固定的类型和大小。

• Image Captioning - 在这里，假设我们有一个需要文字描述的图像。 所以我们有一个单一图像，一系列或一系列的单词作为输出。 这里的图像可能是固定的大小，但输出是不同长度的描述。

• Language Translation - 这基本上意味着我们有一些特定语言的文本，我们说英语，我们希望用法语翻译它。
  每种语言都有它自己的语义，并且对于相同的句子将具有不同的长度。 所以这里输入和输出的长度是不同的。

因此，RNN可用于将输入映射到不同类型，不同长度的输出，并且在其应用中相当普遍。 看看他们的应用，让我们看看RNN的架构是怎样的。

2，什么是循环神经网络？

假设任务是预测句子中的下一个单词。让我们尝试使用MLP来完成它。那么在MLP中会发生什么？最简单的形式，我们有一个输入层，一个隐藏层和一个输出层。输入层接收输入，应用隐藏层激活，然后我们最终接收输出。参考一步一步理解自然语言处理之word2vec工具相关算法演进

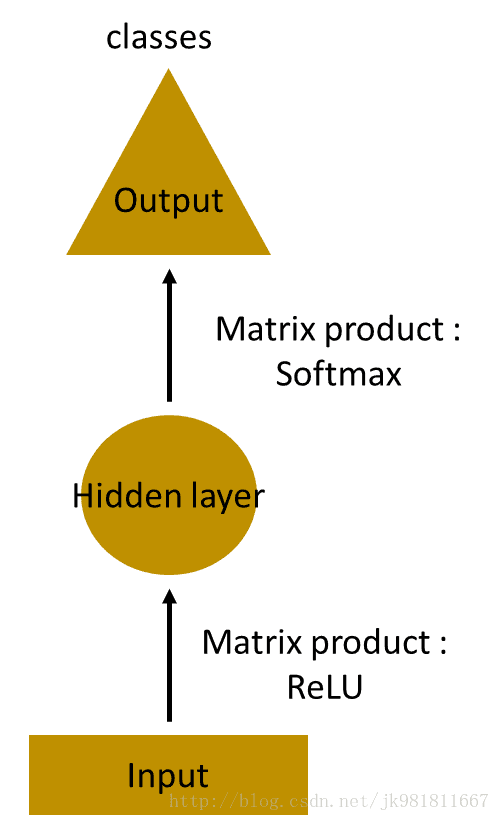
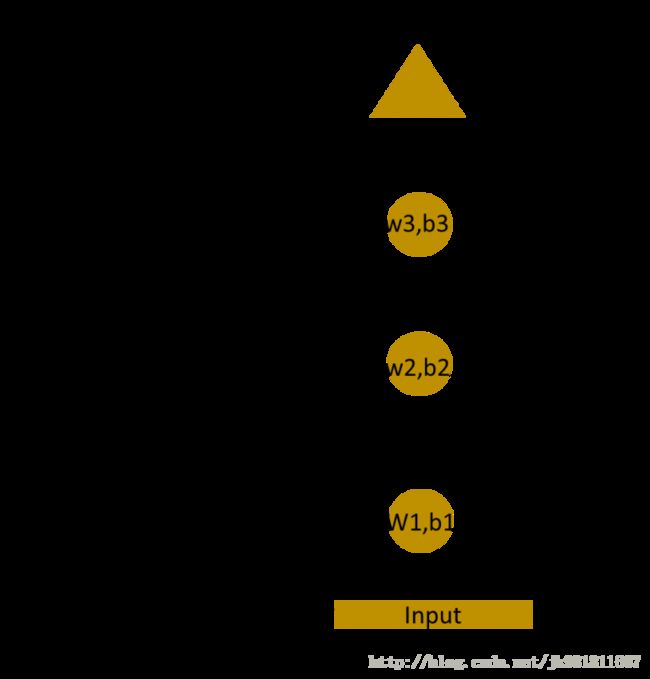
让我们有一个更深的网络，其中存在多个hidden layers。因此，在这里，输入层接收输入，首先应用hidden layer激活，然后将这些激活发送到下一个hidden layer，并通过层连续激活以产生输出。每个hidden layers都有自己的 weights 和 biases。

由于每个隐藏层都有自己的权重和激活，所以它们的行为是独立的。我们期待的结果是连续输入之间有关系的序列。我们可以提供隐藏层的输入吗？我们可以！

这里，这些隐藏层的权重和biases是不同的。因此，这些层中的每一个都独立行为，不能组合在一起。为了将这些隐藏层结合在一起，我们将对这些hidden layers具有相同的权重和biases。

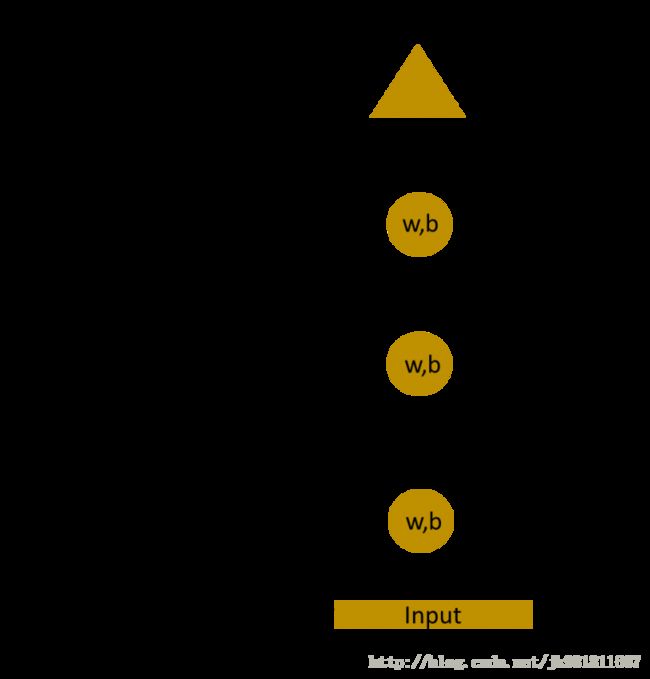
现在我们可以将这些层合并在一起，所有隐藏层的权重和偏差是相同的。所有这些隐藏的层可以在一个单一的循环层中一起滚动。

所以这就像将输入提供给隐藏层。在任何时候，循环神经元的步长权重将是相同的，因为它现在是一个单一的神经元。所以一个经常性神经元存储先前输入的状态并与当前输入结合，从而保持当前输入与先前输入的一些关系。

3，理解一个循环神经元的细节

首先，我们要做一个简单的任务。我们有一个词“hello”。 所以我们提供前4个字母，即h，e，l，l，并要求网络预测最后一个字母，即’o’。 所以这里任务的词汇只有4个字母{h，e，l，o}。 在涉及自然语言处理的实际情况下，词汇表包括整个维基百科数据库中的词语，或者一种语言中的所有词语。 这里为了简单，我们已经采取了一小部分词汇。

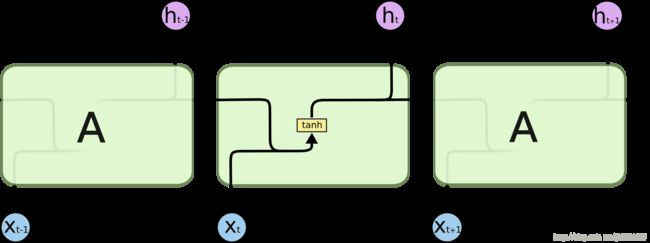
让我们来看看如何使用上面的结构来预测单词“hello”中的第五个字母。 在上面的结构中，蓝色的RNN块将一个叫做递归公式的东西应用到输入矢量，也是它的前一个状态。 在这种情况下，字母“h”没有任何前面的字母。
因此，当字母“e”被提供给网络时，对字母“e”和前一个字母“h”的状态应用递推公式。 这些被称为输入的各个时间步骤。
所以如果在时间t，输入是“e”，在时间t-1，输入是“h”。 递推公式适用于e和h两者。 我们得到一个新的状态。

当前状态的公式可以写成 -

在这里，Ht是新的状态，ht-1是之前的状态，而xt是当前的输入。 我们现在有一个以前的输入状态，而不是输入本身，因为输入神经元会在我们以前的输入上应用变换。 所以每个连续的输入都被称为时间步。

在这种情况下，我们有四个输入给网络，在递推公式中，每个时间步将相同的功能和相同的权重应用于网络。

以最简单的递归神经网络形式来说，激活函数是tanh，递归神经元的权重是Whh，输入神经元的权重是Wxh，我们可以写出时间t的状态方程为 -

在这种情况下，循环神经元只是考虑了前一个状态。 对于更长的序列，公式可能涉及多个这样的状态。 一旦计算出最终状态，我们就可以继续生成输出

现在，一旦计算出当前状态，我们就可以计算出输出状态

让我总结一个经常性神经元中的步骤 -

1. 输入的一个时间步骤被提供给网络，即xt被提供给网络
2. 然后，我们使用当前输入和前一个状态的组合来计算其当前状态，即我们计算ht
3. 当前的ht在下一个时间步成为ht-1
4. 我们可以按照问题所要求的时间步长进行处理，并结合之前所有状态的信息
5. 一旦所有的时间步骤完成，最终的当前状态被用来计算输出yt
6. 然后将输出与实际输出进行比较，并生成错误
7. 然后将误差反向传播到网络来更新权重（我们将在后面的章节中详细介绍反向传播），并对网络进行训练

我们来看看如何在Excel中计算这些状态并获得输出。

4，Excel中循环神经元的正向传播

我们首先看看输入

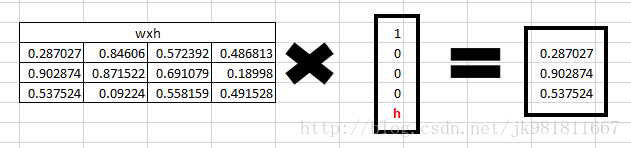
输入是一个one-hot编码。 我们的整个词汇是{h，e，l，o}，因此我们可以很容易地对输入进行one-hot编码。

现在输入神经元将使用权重wxh将输入转换为隐藏状态。 我们已经随机地将权重初始化为3 * 4矩阵 -

Step1：

现在对于字母“h”，对于隐藏状态，我们需要Wxh * Xt。 通过矩阵乘法，我们得到它

Step2：

现在转向循环神经元，我们有Whh作为1 * 1矩阵的权重0.427043，而bias也是1 * 1矩阵0.567001。

对于字母“h”，之前的状态是[0,0,0,0]，因为之前没有字母。
所以要计算 - Whh * ht-1 +bias

Step3：

现在我们可以得到当前的状态为：

因为对于输入”h”字母，没有以前的隐藏状态，我们将tanh函数应用到这个输出并得到当前状态 。

Step 4:

现在我们继续下一个状态。 现在“e”被提供给当前网络。 上一步的ht的处理输出现在变成ht-1，而一个one-hot的e是xt。 现在我们来计算当前状态ht。Whh，Wxh这个权重值和上一步一样。

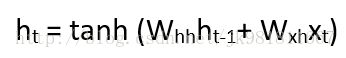
计算：Whh*ht-1 +bias

计算：Wxh*xt

Step 5:

现在我们计算字母“e”的ht.

现在”e”的ht将成为下一个状态的ht-1，而循环神经元会和新的字母一起使用它来预测下一个状态。

Step 6:

在每个状态下，循环神经网络也会产生输出。 我们来计算字母e的yt。

Step 7:

可以通过应用softmax函数来计算词汇表中特定字母的概率。 所以我们应该有softmax（yt）。可以看出，h字母的概率0.419748最高。（我们想要的结果是e字母的概率是1，理想中的结果是[0,1,0,0]）现在考虑如何更新权重，使得我们e字母的概率最高。使用误差反向传播,参考 一步一步分析讲解神经网络基础-backpropagation algorithm

现在我们面临的下一个BIG问题是如何在递归神经网络的情况下进行反向传播。 如果有反馈循环，权重是如何更新的？

5，在RNN中的反向传播（BPTT）

想象一下如果循环神经网络如何更新权重，可能会有一些挑战。 因此，为了理解和可视化反向传播，让我们在所有时间步骤展开。 在RNN中，我们可能在每个时间步骤都可能有输出，也可能没有输出（如第一步字母“h”没有输出）。

在正向传播的情况下，输入在每个时间步进入和前进。 在这种情况下，如果发生向后传播，我们在时间上反过来来改变权重，所以我们称之为反向传播时间（BPTT）。

在一个RNN中, 预测值 ȳt， yt真实值。误差使用 cross entropy loss：

Et(ȳt,yt) = – ȳt log(yt)

E(ȳ,y) = – ∑ ȳt log(yt)

我们通常把整个序列（单词）当作一个训练样例，所以总误差只是每个时间步长（字符）处误差的总和。 我们可以看到的权重在每个时间步都是一样的。 让我们总结反向传播的步骤。

1. 交叉熵误差首先使用当前输出和实际输出来计算
2. 请记住，网络在所有时间步骤都展开。
3. 对于展开的网络，相对于权重参数为每个时间步骤计算梯度。
4. 现在所有时间步长的重量都是相同的，所有时间步长的梯度可以组合在一起。
5. 然后权重被更新为循环神经元和全连接层

展开的网络看起来很像一个普通的神经网络。反向传播算法与常规神经网络类似，只是将所有时间步长的误差梯度组合在一起。现在如果有100多个时间步骤，你会怎么想呢？由于展开网络变得非常庞大，这对于网络来说基本上需要很长的时间。

如果您不想深入反向传播的数学，您需要了解的是，一旦您展开网络中的循环神经元，通过时间的反向传播与常规神经网络中的反向传播类似。详情请看一步一步分析讲解神经网络基础-backpropagation algorithm

基本的RNN网络到此讲解完。来一条分隔线，我不建议一次性读完blog,充分理解上述基础的RNN网络，才能顺利开始下面的内容。

==========================分隔线=============================

6，梯度消失，长期依赖问题

RNN的工作原理是信息的结果取决于其以前的状态或前n个时间步骤。规则的RNN可能难以学习远距离依赖。看个例子，”The man who ate my pizza has purple hair”. 描述紫色头发的男人，而不是吃披萨的男人。所以这是一个长期的依赖。

如果我们在这种情况下反向传播错误，则需要应用链式规则。要计算第三个时间段后的错误，

在这里，我们应用链规则，如果任何一个梯度接近0，由于乘法，所有的梯度将急剧地指数地快速为零。这种状态将不再有助​​于网络学习任何东西。这被称为消失梯度问题。

与渐变梯度问题相比，消失梯度问题更具威胁性，梯度问题由于单梯度或多梯度值变得非常高而变得非常大。

消失梯度问题更重要的原因是通过将梯度限制在预定义的阈值，可以容易地解决爆炸梯度问题。幸运的是，还有办法可以处理渐变渐变问题。有像LSTM（长期短期记忆）和GRU（门控循环单元）这样的架构可以用来处理消失梯度问题。

正如我们所看到的，当我们要求他们处理长期的依赖性时，RNN遭受渐变问题的消失。随着参数的数量变得非常大，它们也变得非常难以训练。如果我们展开网络，它变得如此巨大，以至于它的融合是一个挑战。

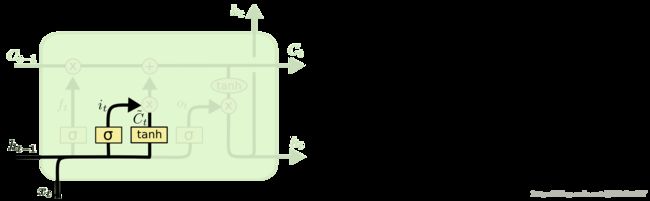
长期短期记忆网络 - 通常被称为“LSTM” - 是一种特殊的RNN，能够学习长期的依赖关系。他们由Hochreiter＆Schmidhuber介绍。他们在各种各样的问题上工作非常好，现在被广泛使用。 LSTMs也有这样的链结构，但重复模块有一个稍微不同的结构。而不是有一个单一的神经网络层，有多层，以一种非常特殊的方式进行交互。他们有一个输入门，一个忘记门和一个输出门。我们将很快提出有关LSTM的详细文章。

7，理解 LSTM Networks

标准RNN中的重复模块包含单个图层。

LSTM也有这样的链式结构，但重复模块结构不同。 不是一个单一的神经网络层，共有四个，在一个非常特殊的方式进行交互。

不要担心发生了什么事情的细节。 稍后我们将逐步解释LSTM图。 现在，让我们试着去熟悉我们将要使用的符号。

在上面的图中，每行包含一个完整的向量，从一个节点的输出到另一个节点的输入。 粉色圆圈表示逐点运算，如向量加法，乘法，而黄色方框表示学习神经网络层。 合并行表示拼接，而分叉表示其内容被复制，副本将转到不同的位置。

The Core Idea Behind LSTMs（构建LSTMs核心设计）

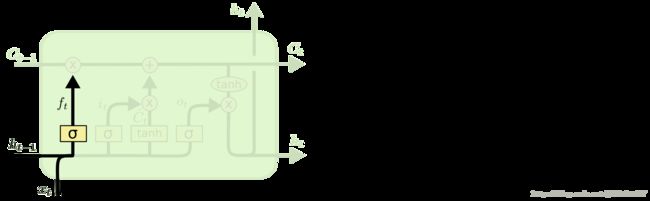
LSTMs的关键是cell state，水平线贯穿图的顶部。

cell state有点像传送带。 它贯穿整个链条，只有一些次要的线性交互作用。 信息非常容易地不变地流过。

LSTM确实有能力去除或增加cell state的信息，由称为gates的结构。

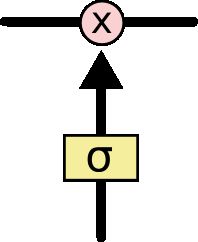
gates是一种可以让信息通过的方法。 它们由S形神经网络层和逐点乘法运算组成。

sigmoid层输出0到1之间的数字，描述每个组件应该通过多少。 值为0意味着“let nothing through”，而值1意味着“let everything through!”

一个标准的LSTM有三个gates，用来保护和控制cell state。

Step 1

决定我们要从cell state中扔掉哪些信息。
这个决定是由一个称为“forget gate layer.”的S形图层来完成的。它看起来是ht-1
和xt，并且针对cell 状态Ct-1中的每个号码输出0和1之间的数字。

Step 2

决定我们要在单元状态中存储什么新的信息。这有两个部分。首先，称为“input gate layer”的S形图层决定我们将更新哪些值。
接下来，tanh层创建一个新的向量C〜t，添加到该cell中。在下一步中，我们将结合这两者来创建状态的更新。

Step 3

现在是时候将旧的单元状态Ct-1更新为新的单元状态Ct。 以前的步骤已经决定要做什么，我们只需要真正做到这一点。
我们用ft乘以Ct-1表示：需要丢弃多少信息量。
我们it* C〜t表示需要添加的信息量。
两者的和，就是新的cell state，Ct，我们决定更新每个状态值的比例。

Step 4

最后，我们需要决定我们要输出什么。 这个输出将基于我们的cell state，但将是一个过滤版本。 首先，我们运行一个S形图层，决定我们要输出的cell state的哪些部分。 然后，我们把cell state通过tanh函数（把值推到-1到1之间）并将其乘以S形门的输出，以便我们只输出我们决定的部分。

标准的LSTM network核心讲完啦。

8， 基于LSTM Network 演化网络

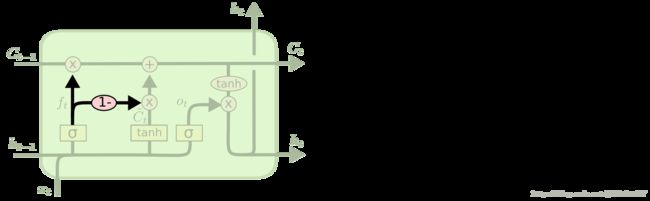
第一个版本变化：Gers＆Schmidhuber（2000）介绍的一种流行的LSTM变体是增加了“peephole connections.”，这意味着我们让gate layers（标准的LSTM一共有三个gate 层，forget gate ，input gate ，output gate ）看到cell state。和上述公式对比多了cell state的状态。

第二个版本变化：是使用耦合的忘记和输入门（ coupled forget and input gates）。 和标准LSTM的区别是：忘记什么信息，增加什么新信息，一起决定新增信息。

第三个版本变化：LSTM稍微更加剧烈的变化是由Cho等人引入的门控循环单元（GRU Gated Recurrent Unit）。（2014）。 它将forget gate 和input gate 结合成一个“update gate.”，它还合并了cell state 和 hidden state，并做了一些其他更改。 由此产生的模型比标准的LSTM模型更简单，并且越来越受欢迎。

这些只是一些最显着的LSTM变体。 还有很多其他的，比如Yao等人的Depth Gated RNNs。（2015年）。 还有一些完全不同的方法来解决长期的依赖问题，比如Koutnik等人的“ Clockwork RNNs”。（2014）。

哪个变种最好？ 差异很重要吗？ Greff等人 （2015）对流行的RNN变体进行了很好的比较，发现它们大致相同。 Jozefowicz等人 （2015）测试了超过一万个RNN变体，发现一些在特定任务上比LSTM更好。

reference：
http://colah.github.io/posts/2015-08-Understanding-LSTMs/
https://www.analyticsvidhya.com/blog/2017/12/introduction-to-recurrent-neural-networks/
https://towardsdatascience.com/understanding-recurrent-neural-networks-the-prefered-neural-network-for-time-series-data-7d856c21b759