机器学习里面通常需要寻找代价函数的最小值，所有如果可以把图形绘制出来，对于初学者分析起来就会简明很多。
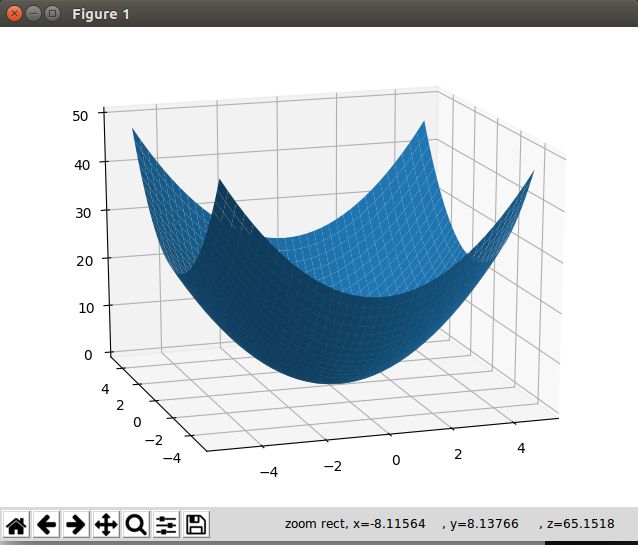
下面取一个例子，绘制z=x²+y²，（x，y的取值范围是 [-5,5] )
实现的代码：
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from mpl_toolkits.mplot3d import Axes3D
#创建一个Axes3d对象
fig=plt.figure()
ax=Axes3D(fig)
#x，y的取值返回是从-5到+5，每隔0.25取一个点
x=np.arange(-5,5,0.25)
y=np.arange(-5,5,0.25)
#[X,Y] = meshgrid(x,y) 将向量x和y定义的区域转换成矩阵X和Y，
#这两个矩阵可以用来表示mesh和surf的三维空间点以及两个变量的赋值。
#其中矩阵X的行向量是向量x的简单复制，而矩阵Y的列向量是向量y的简单复制。
x,y=np.meshgrid(x,y)
#r=np.sqrt(x**2+y**2)
#z=np.sin(r)
z=x**2+y**2
#plot_surface 是绘制一个平面 ax.scatter 是绘制点
surf=ax.plot_surface(x,y,z)
plt.show()
绘制的结果：
2017-05-28 18-37-21屏幕截图.png
补充
1. 对于x,y=np.meshgrid(x,y) 函数作用的分析：
例如， 要在“3<=x<=5，6<=y<=9，z不限制区间” 这个区域内绘制一个3D图形，如果只需要整数坐标为采样点的话。我们可能需要下面这样一个坐标构成的矩阵：
(3,9),(4,9),(5,9);
(3,8),(4,8),(5,8);
(3,7),(4,7),(5,7);
(3,6),(4,6),(5,6);
我们可以这样描述这个坐标矩阵：
把各个点的x坐标独立出来，得：
3,4,5;
3,4,5;
3,4,5;
3,4,5;
再把各个点的y坐标也独立出来：
9,9,9;
8,8,8;
7,7,7;
6,6,6;
这样对应的x、y结合，便表示了上面的坐标矩阵。meshgrid就是产生这样两个矩阵，来简化我们的操作。然后根据(x, y)计算获得z，并绘制出三维图形。