字符串 KMP算法
前言
KMP,作为字符串的入门算法,还是比较有难度的。起码当初我尝试理解KMP的时候,就花了整整一个上午去翻阅各种博客。虽然每一篇博客在理解之后再去看会发现说得都挺有道理,但是在云里雾里的时候,并不是所有的博客都能一语点破雾水。
特将学习体会记录下来(>人<;)
KMP用来干什么?
KMP算法,是一种字符串的单模匹配算法。说白了,就是在s1串中去找s2串。
看吧,其实名字高大上,本质上就是判重..
朴素算法的低效性
假如没有KMP,我们要怎么处理这种问题?
枚举每一个开头,然后从每一个开头来尝试是否是字串?
参照下面这个例子。
这个例子比较极端,但是能比较好的阐述KMP的优越性
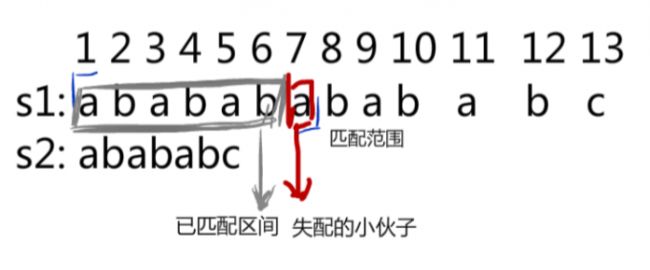
好了,我们尝试用朴素算法处理单模匹配。
- 从s1的1a开始,发现匹配得上
- 1a到6b一直能匹配上
- 7a失配,从1a开始尝试匹配字串失败
- 重新从2b开始尝试匹配,发现失配
- 从3a开始尝试....失败应该都能看出来吧
- 不断不断地重复中...(*  ̄︿ ̄)
- 终于,s2发现,从7a开始才能匹配上
- 至此,完成了朴素算法的一轮匹配
可以发现,假如数据更加极端,朴素算法的效率也会成倍的放大。在最劣情况下,复杂度可以达到O(s1长度\(\times\)s2长度),并且这种数据也是相当好造(上述就是一个例子),所以说朴素算法基本上可以被废弃了
KMP算法的优越性
回顾刚刚的匹配过程,哪里可以优化呢?
最长公共前后缀思想
可以发现,辛辛苦苦匹配了很长的“已匹配区间”,仅仅因为一个“失配因子”,就要全部推翻重来。并且在下一次的匹配中,上一次的“已匹配区间”完全没能利用上。
这部分“已匹配空间”虽然占用了匹配时间,但是仅仅发挥了一次作用。很明显,这种匹配思路不尽合理。我们应当想法设法,把所以已匹配上的信息利用好。
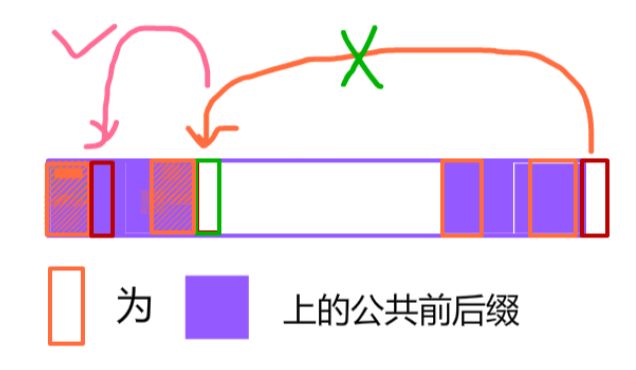
对于例子中给出的“已匹配区间”,我们发现左面有连续的4个abab,右面也有连续的4个abab。假如我们下一次直接从右面的abab开始接着匹配,那么就省下了重复匹配这个abab的过程。
在此,引入一个概念 “最长公共前后缀”
前缀是什么?
前缀就是指对于长度为n的字符串,从前面开始长度为\(1 \rightarrow (n-1))\)的所有字串
"tesn"的所有前缀依次为:t,te,tes
后缀是什么?
后缀就是指对于长度为n的字符串,从后面开始长度为\(1 \rightarrow (n-1))\)的所有字串
"test"的所有后缀依次为:esn,sn,n
那么,什么是公共前后缀?
顾名思义,就是在全部前后缀中,相同的一对
ababab的前缀依次为:a,ab,aba,abab,ababa
后缀依次为:babab,abab,bab,ab,b
那么它的公共前后缀就有:ab,abab
最长公共前后缀呢?就是“最长”的公共前后缀
例如,ababab的最长公共前后缀就是abab
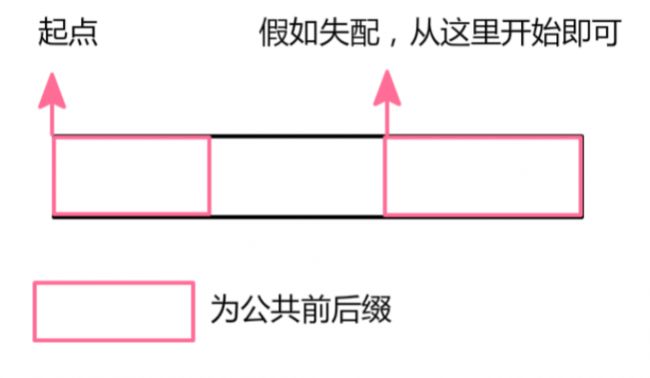
了解最长公共前后缀之后,再回到匹配区间上。
在一段匹配区间中,由于前缀与后缀有相同部分,于是后缀便可以直接用作下一个区间的前缀。类似于整体平移
为了最大化利用匹配区间上已经匹配过的信息,我们就找到当前区间的最长公共前后缀。这样一来,下一次匹配就有了经可能大的“基础”,匹配起来就会快一些
(到这一步,初学者可能会有些困惑,甚至举出了挑战正确性的“反例”。坚持看下去!( o=^•ェ•)o ┏━┓)
失配指针
我们把在每一个节点失配时,应当跳向的下一个节点取名为当前节点的失配指针。失配指针指向的便是字串的最长公共前后缀的末坐标。
注意!失配指针指的不是当前节点的失配,而是当前节点的下一个节点失配时的处理情况。
怎么批处理出失配指针?分类讨论
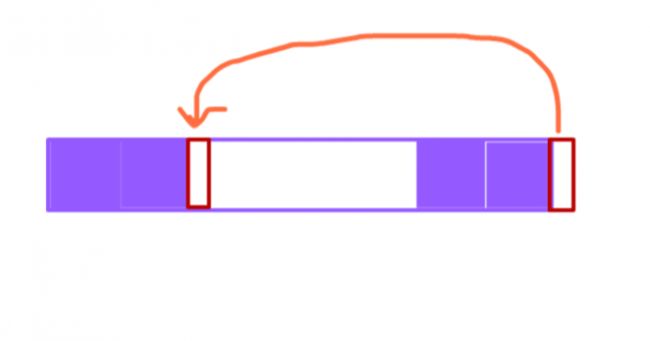
假设当前匹配到了u节点
· 如果u+1节点与fail[u]+1节点相同,那么fail[u+1]=fail[u]+1
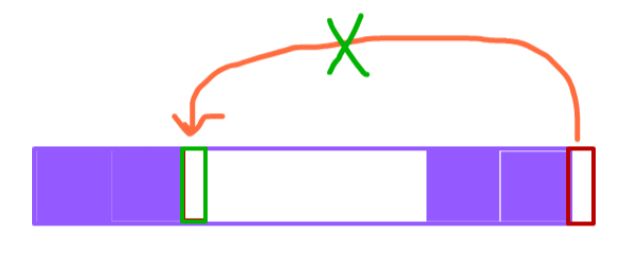
· 如果u+1节点不等于fail[u]+1节点!
怎么办?不慌!由于公共前后缀的公共前后缀同样满足公共的性质,所以我们递归即可。
· 那假如到头也没能找到公共前后缀?那就将它的失配指针指向root=0即可
嗯,思路就是这样,代码如下:
// 第一个不用建,因为fail肯定指向root=0
for(int i=2;i<=lenb;++i){
int tmp=fail[i-1];
//如果失配
while(tmp!=0&&b[tmp+1]!=b[i]){
tmp=fail[tmp];
}
fail[i]=tmp;
if(b[tmp+1]==b[i]) fail[i]++;
}
匹配
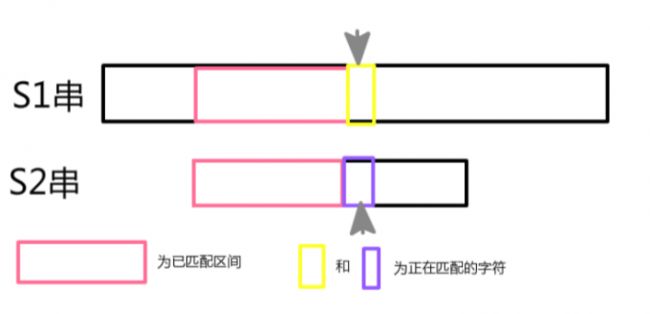
有了,失配指针,怎么快速匹配?
KMP的另一个精髓就是:只有s2指针可能回档,s1指针只会前进
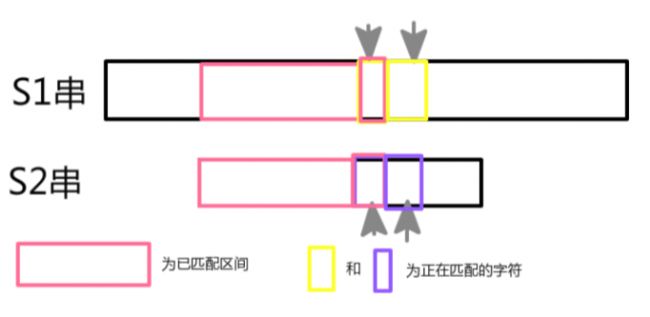
如果匹配上了:
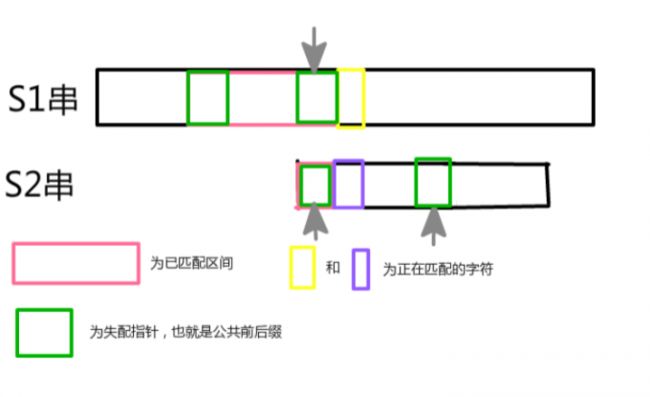
反之如果失配了,就要跳失配指针:
酱紫匹配下去,当s2指针==s2长度时,就说明成功匹配了一个字串!( ̄y▽, ̄)╭
技巧或忠告
-
strlen的效率并不是非常高,请无比多声明一个len变量,而不要每一次都调用strlen()函数。否则一个正确的算法可能会因为这一个小点而tle6个点
-
当成功在s1串中匹配到一个s2串之后,如果还需要继续匹配,可以为s2指针来一个失配转移,而不是直接归为0。算是小优化技巧
完整代码
#include
#include
#include
#include
using namespace std;
const int MAX=2e6+5;
char a[MAX],b[MAX];
int fail[MAX];
int x,y,lena,lenb;
int main(){
freopen("test.in","r",stdin);
scanf("%s%s",a+1,b+1);
lena=strlen(a+1); lenb=strlen(b+1);
for(int i=2;i<=lenb;++i){
int tmp=fail[i-1];
while(tmp!=0&&b[tmp+1]!=b[i]){
tmp=fail[tmp];
}
fail[i]=tmp;
if(b[tmp+1]==b[i]) fail[i]++;
}
x=0;
for(int i=1;i<=lena;++i){
if(a[i]==b[x+1]){
x++;
if(x==lenb){
printf("%d\n",i-lenb+1);
x=fail[x];
}
}
else{
while(x!=0&&b[x+1]!=a[i]){
x=fail[x];
}
if(b[x+1]==a[i]) x++;
}
}
for(int i=1;i<=lenb;++i) printf("%d ",fail[i]); puts("");
return 0;
}
应用:求字符串的最小循环节
字符串的最小循环节嘛,定义没什么好说的
一个重要的性质:
\(字符串存在长度为s的循环节 \iff s(l,r-s) = s(l+s,r)\)
应该很好理解吧( ̄︶ ̄*))
那么假如字符串存在最小的循环节,长度为\(s'\),那么就存在"最长的公共前后缀"\(s(l,r-s') = s(l+s',r)\)
而失配指针求的正是这个“最长公共前后缀”。如此一来不就一石二鸟了嘛
反之,如果字符串不存在循环节,那么整个字符串长度一定不能被公共前后缀余下的区间长度整除
后记
KMP第一次学有些难以理解,但是好好理解理解,还是一个好写好调的模板
至此,KMP总结完毕!(〃` 3′〃)