后缀数组

字符串 后缀数组

后缀数组——处理字符串的有力工具 2009年国家集训队论文

前言

后缀数组真的是个神仙东西。学这个东西之前千万不要抱着以下想法

· 欸，晚饭吃撑了没事干，学个后缀数组玩玩..

· 嗯，学完这个算法，我就去摸鱼》。

否则，真的会死人！ 推荐找一个心情舒畅，神志清晰的大段时间，准备好大剂量咖啡后在和后缀数组硬刚。

本人才疏学浅，因个人理解不够，或是语言组织不佳，导致的语意跳跃不连贯，敬请谅解！

本文重要参考资料（无先后顺序）

· 2009年国家集训队论文 提取码：76mg

· 后缀数组 最详细(maybe)讲解

感谢先人们的大力奉献！

后缀数组 \(part 1\) (get_sa)

这部分推荐看博客学习。因为集训队论文实在是太神仙了

定义部分（sa && rak）

规定suff(i)表示从下标为i的位置开始的后缀

然后是后缀数组中两个非常重要的数组： rak[]和sa[]

首先将所有的后缀按照字典序排序

sa[i]指的是排名第i的后缀在的起始坐标

rak[i]指的是起始坐标为i的后缀的排名

sa数组结果如下:

sa数组	结果	意义
sa[1]	4	排名第1的后缀下标为4，suff(4)=I
sa[2]	2	排名第2的后缀下标为2，suff(2)=MOI
sa[3]	3	排名第3的后缀下标为3，suff(4)=OI
sa[4]	1	排名第4的后缀下标为1，suff(1)=YMOI

rak数组结果如下：

rak数组	结果	意义
rak[1]	4	下标为1的后缀排名第4，suff(1)=YMOI
rak[2]	2	下标为2的后缀排名第2，suff(2)=MOI
rak[3]	3	下标为3的后缀排名第3，suff(1)=OI
rak[4]	1	下标为4的后缀排名第1，suff(1)=I

嗯，引例至此，应该还算清晰吧 ο(=•ω＜=)ρ⌒☆

倍增求解

后缀数组貌似有倍增和DC3两种求法，不过本人蒟蒻，只会倍增（＞人＜；）

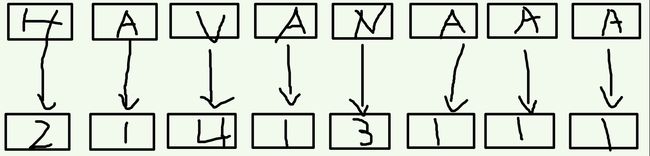
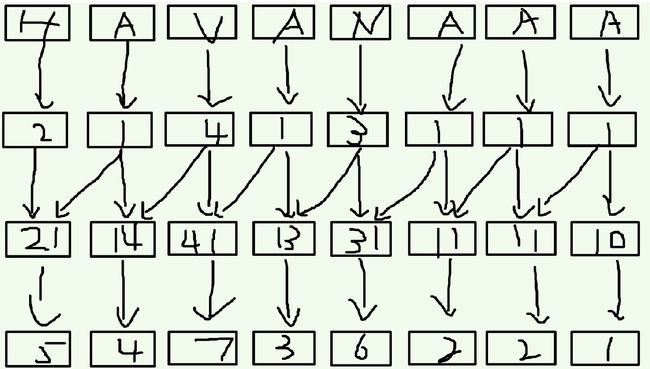
懒得画图，从别人的博客上盗的图片

发现有好多博客都有这张图片，不知道版权所有者是谁。如果您觉得以下的引用冒犯到了您的版权，请联系[email protected]

首先，我们为字符串每一个位置开始，排一个长度为1的字串的rak值。这里直接用ASCII码就好

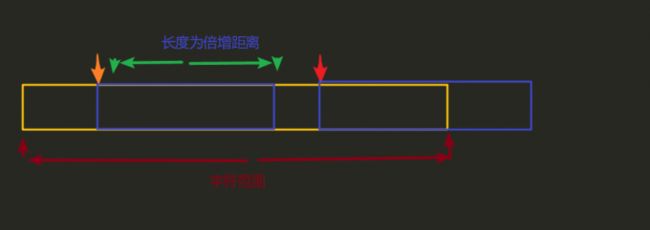
接着，倍增下去。在这个例子中，我们开始处理长度为(1*2=2)的字串

利用好上一回的rak值，把倍增范围后的rak值挪过来做第二关键字。

此时，假如已经排好了长度为k的字串，此时要开始排长的为2*k的字串。那么，对于下标为i的后缀，它的第一关键词是rak[i],第二关键词是rak[i+k]。

然后与处理十进制类似，处理以下m进制的这n个双关键子，排序后的顺序即为新一轮的rak值

如此倍增下去，就可以求出来rak了！

基数排序

考量以下复杂度。倍增复杂度\(O(\log_n)\),排序复杂度\(O(n\log_n)\),总复杂度\(O(nlog^2_n)\)

￣へ￣不是非常优秀

那么怎么去优化呢？可以再次基础上加上基数排序

基数排序这个东西思路非常好理解。

1. 回归问题，我们要处理的总是两位的m进制排序。
2. 我们建m个桶，第一次按照第二关键字信息，将这n个数压入桶中，然后再按照顺序取出。此时的序列就保证了第二关键字的单调递增
3. 我们将m个桶初始化，再按照第一关键字信息，将n个数重新再压入到桶中。此时，对于同一个桶(第一关键字相同)内的数组，可以保证第二关键字递增，即桶内的数字单调递增。我们再将这m个桶中的顺序按顺序全倒出来就ok

例子如下：

16 25 32 62 21 79 38 18 71

首先按照第二关键字排序：

桶	数字
0
1	21,71
2	32,62
3
4
5	25
6	16
7
8	38,18
9	79

取出数字： 21 71 32 62 25 46 38 18 79

然后按照第一关键字排序：

桶	数字
0
1	18
2	21,25
3	32,38
4	46
5
6	62
7	71,79
8
9

取出数字： 18 21 25 32 38 46 62 71 79

完成(≧∇≦)ﾉ

get_sa 代码

思路会了之后，代码实现也依旧是一个难点，看注释尝试理解一下

我已经将字符串存在了s[]中，从1开始；n保存着的是字符串长度

void get_sa(){
	m=122; //表示桶的大小，即m进制。 通常第一次处理时开m=122是足够的
	// 接下来是长度为1的字串的后缀排序
	for(int i=1;i<=m;++i) buc[i]=0; // 初始化桶 并没有什么卵用，纯粹为了看着舒适
	for(int i=1;i<=n;++i) buc[x[i]=s[i]]++; // x的意义就是rak 这里将ascii码赋值给x，然后给那个值的桶++
	for(int i=2;i<=m;++i) buc[i]+=buc[i-1]; // 计算出x为i的后缀的排序范围，为下一行服务 （难理解！手推出真理！）
	for(int i=n;i>=1;--i) sa[buc[x[i]]--]=i; // 为sa赋值。 规定：越靠后，相同条件下sa越小
	// 然后开始倍增处理
	for(int k=1,t=1;t<=20;++t,k<<=1){
		p=0;
		for(int i=n-k+1;i<=n;++i) y[++p]=i; // 这里是指有一些第二关键字是0的直接进队
		for(int i=1;i<=n;++i) if(sa[i]>k) y[++p]=sa[i]-k; // 有第二关键字的按照顺序进队
		for(int i=1;i<=m;++i) buc[i]=0; //接下来三行与第一次处理时意义相同
		for(int i=1;i<=n;++i) buc[x[i]]++;
		for(int i=2;i<=m;++i) buc[i]+=buc[i-1];
		for(int i=n;i>=1;--i) sa[buc[x[y[i]]]--]=y[i]; // 如果一个值的第二关键字排序后靠后出现，那么它的sa值也应当同条件下偏大
		swap(x,y); //y数组没有用了，而求新的x数组正好需要用到旧的x
		x[sa[1]]=1; p=1;  //处理以下边界
		for(int i=2;i<=n;++i) x[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])?p:++p; 
			// x是rak值，很明显有一些后缀在当前长度的排序是完全相同的，它们的x值应该相同
			// 判断语句判断的就是第一关键字与第二关键字是否相同。如果完全相同说明后缀完全重复，排名就应当相同
			// 否则排名后移
		if(p==n) break; // 小优化，如果排名的最后一名等于字符串长度，那么说明排序完成
		else m=p; // 否则更新一下桶的大小，准备下一轮倍增
	}
}

Q&A：

Q:sa[i]+k和sa[i-1]+k不怕越界嘛？

x[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])?p:++p;

A:嘿，还真不怕。

发现如果sa[i]+k和sa[i-1]+k越界了，那么y[sa[i]]和y[sa[i-1]]是绝对不可能匹配得上的，而根据&&运算符的特点，如果前一个条件没能满足，那么是不会执行后面的语句的

但是！肯定有细心的小朋友会说，“假如后面的区间正好卡在边界上，还判断通过了，那么下一次判断不就肯定会越界嘛？”

嗯，好问题。事实上，的确是这样的。它就是会越界。但是它只可能越界一个单位，所以数组多开一点，然后设置一个与别的rak值绝对不可能相同的值即可。（初始化未零就不错）

Q:既然x的意义是rak，那么为什么不能直接用rak替代rak？

A:好问题，我也正在寻找答案中。我尝试了几遍，不论从理论上还是结果上都找不出毛病。不过所有的博客都可以设了x数组，包括国家集训队的论文，所以我猜肯定是有原因但我没发现吧ヽ(*。>Д<)o゜

后缀数组 \(part 2\) (get_height)

这部分内容请参考集训队论文。因为博客有错误，并且论文解释得比较清晰

嗯，把sa和rak求出来了，然后呢？摆着看？很明显不是。在这里，我们引入“最长公共前缀”——\(LCP\)

什么是LCP？

\(LCP(i,j)=suff(sa[i])和suff(sa[j])的最长公共前缀\)

LCP简单性质

1. \(LCP(i,j)=LCP(j,i)\)
2. \(LCP(i,i)=len(sa[i])=n-sa[i]+1\)

嗯，很明显，这就是“很明显的”东西。那么浪费时间去重复他干什么？

1. 套用性质一，我们可以将i>j的情况转化为j
2. 套用性质二，我们可以直接求出i=i的情况

也就是说，我们只需要专心解决i

LCP性质1

性质：\(LCP(i,j)=\min(LCP(i,k),LCP(k,j)) k\in[i,j]\)

尝试证明如下：

设\(p=min(LCP(i,k),LCP(k,j))\)，那么就有\(LCP(i,k)\geq p\),\(LCP(k,j)\geq p\)

\(\because suff(sa[i])与suff(sa[k])的前p位相等\)

\(又\because suff(sa[k])与suff(sa[j])的前p位相等\)

\(\therefore suff(sa[i])与suff(sa[j])的前p位相等\)

假设\(LCP(i,j)=q>p\),即\(q\geq p+1\),可推理得\(suff(sa[i])[p+1]=suff(sa[j])[p+1]\)

但是\(\because suff(sa[i])[p+1]\neq suff(sa[k])[p+1]或者suff(sa[k])[p+1]\neq suff(sa[j])[p+1]\)

\(\therefore suff(sa[i])[p+1]\neq suff(sa[j])[p+1]\)

推理出矛盾，所有假设不成立。性质得以证明！φ(゜▽゜*)♪

LCP性质2

性质：\(LCP(i,j)=\min(LCP(k,k+1)) k\in [i,j)\)

这个结合LCP性质1就比较好理解了

把\(LCP(i,j)\)拆成\(\min(LCP(i,i+1),LCP(i+1,j))\)，套用LCP性质1

接着拆\(LCP(i+1,j)\)，循环套用LCP性质1

顺利证明！

LCP的求法

我们设\(height[i]=LCP(i-1,i)\)

一个显然的事实是：\(height[1]=0\)

套用LCP性质2，可知:\(LCP(i,j)=\min(height[i]) i\in [i+1,j]\)

我们便将问题由LCP的求解转移到了height的求解。

那height怎么求？枚举？ 明显扯淡 非也

我们接着设\(h[i]=height[rak[i]]\)

经过简单的推演，可以发现\(h[i]=height[rak[i]],height[i]=h[sa[i]]\)

说得通俗一些

数组	意义
\(height[]\)	求排好序之后，排名为i的后缀和前一位的最长公共前缀
\(h[]\)	求未排好序之前，下标为i的后缀和前一位的最长公共前缀

接着，我们来考量一下非常关键的一条性质:

\[h[i]\geq h[i-1]-1 \]

我们不妨设下标为i得后缀按排名来，前一位的下标为k。设\(u=suff(i), v=suff(k)\)

假如u与v的首字母不同，那么\(h[i]=0\)，\(h[i+1]\geq 0\)，因此\(h[i+1]\geq h[i]-1\)

假如u与v的首字母相同。那么对于下标为i+1和k+1的后缀，\(LCP(rak[i+1],rak[k+1])=LCP(rak[i],rak[k])-1\)。想一想，为什么v会排在u的前面？由于u和v的首字母相同，那么按照字典序\(suff(k+1)\)肯定小于\(suff(i+1)\)。因此\(rak[k+1] 根据LCP性质1，可以得知\(LCP(rak[k+1],rak[i+1])=height[rak[i]]-1<=LCP(rak[i+1]-1,rak[i+1])=height[rak[i+1]]\) 因此\(height[rak[i+1]]\geq height[rak[i]]-1\)

code:

void get_height(){
	for(int i=1;i<=n;++i) rak[sa[i]]=i; //首先线性的把rak[]求出来
	height[rak[1]]=0; //初始化边界
	int k=0; //表面意思
	for(int i=1;i<=n;++i){ // 利用了h[i]的性质，所有height的求解也要按照字符串未排序前的下标顺序来
		if(rak[i]==1) continue; // 已处理过，跳过
		if(k) k--; // 利用性质 h[i]>=h[i-1]-1 实现伪线性处理
		int j=sa[rak[i]-1]; // 排名后前一位的下标
		while(i+k<=n&&j+k<=n&&s[i+k]==s[j+k]) ++k; // 不断尝试扩大k来获得最优解
		height[rak[i]]=k; //赋值 ok！
	}
}

后缀数组 \(part 3\) (汇总)

完整代码如下：

#include 
#include 
#include 
#include 
using namespace std;

const int MAX=1e6+5;
char s[MAX];
int n,m,p;
int buc[MAX],x[MAX],y[MAX],rak[MAX],sa[MAX],height[MAX];

void input();
void get_sa();
void get_height();

int main(){
	freopen("test.in","r",stdin);

	input();
	get_sa();
	get_height();

	return 0;
}

void input(){
	scanf("%s",s+1); n=strlen(s+1);
}

void get_sa(){
	m=122; //表示桶的大小，即m进制。 通常第一次处理时开m=122是足够的
	// 接下来是长度为1的字串的后缀排序
	for(int i=1;i<=m;++i) buc[i]=0; // 初始化桶 并没有什么卵用，纯粹为了看着舒适
	for(int i=1;i<=n;++i) buc[x[i]=s[i]]++; // x的意义就是rak 这里将ascii码赋值给x，然后给那个值的桶++
	for(int i=2;i<=m;++i) buc[i]+=buc[i-1]; // 计算出x为i的后缀的排序范围，为下一行服务 （难理解！手推出真理！）
	for(int i=n;i>=1;--i) sa[buc[x[i]]--]=i; // 为sa赋值。 规定：越靠后，相同条件下sa越小
	// 然后开始倍增处理
	for(int k=1,t=1;t<=20;++t,k<<=1){
		p=0;
		for(int i=n-k+1;i<=n;++i) y[++p]=i; // 这里是指有一些第二关键字是0的直接进队
		for(int i=1;i<=n;++i) if(sa[i]>k) y[++p]=sa[i]-k; // 有第二关键字的按照顺序进队
		for(int i=1;i<=m;++i) buc[i]=0; //接下来三行与第一次处理时意义相同
		for(int i=1;i<=n;++i) buc[x[i]]++;
		for(int i=2;i<=m;++i) buc[i]+=buc[i-1];
		for(int i=n;i>=1;--i) sa[buc[x[y[i]]]--]=y[i]; // 如果一个值的第二关键字排序后靠后出现，那么它的sa值也应当同条件下偏大
		swap(x,y); //y数组没有用了，而求新的x数组正好需要用到旧的x
		x[sa[1]]=1; p=1;  //处理以下边界
		for(int i=2;i<=n;++i) x[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])?p:++p; 
			// x是rak值，很明显有一些后缀在当前长度的排序是完全相同的，它们的x值应该相同
			// 判断语句判断的就是第一关键字与第二关键字是否相同。如果完全相同说明后缀完全重复，排名就应当相同
			// 否则排名后移
		if(p==n) break; // 小优化，如果排名的最后一名等于字符串长度，那么说明排序完成
		else m=p; // 否则更新一下桶的大小，准备下一轮倍增
	}
}

void get_height(){
	for(int i=1;i<=n;++i) rak[sa[i]]=i; //首先线性的把rak[]求出来
	height[rak[1]]=0; //初始化边界
	int k=0; //表面意思
	for(int i=1;i<=n;++i){ // 利用了h[i]的性质，所有height的求解也要按照字符串未排序前的下标顺序来
		if(rak[i]==1) continue; // 已处理过，跳过
		if(k) k--; // 利用性质 h[i]>=h[i-1]-1 实现伪线性处理
		int j=sa[rak[i]-1]; // 排名后前一位的下标
		while(i+k<=n&&j+k<=n&&s[i+k]==s[j+k]) ++k; // 不断尝试扩大k来获得最优解
		height[rak[i]]=k; //赋值 ok！
	}
}

后记

后缀数组，非人哉

真的好奇当初是哪位神人能发明出后缀数组这种神仙东西

后续打算把所有疑难杂症都解决后好好刷一刷字符串相关的题

记得填坑补上！！