图的最短路径-Dijkstra算法和Floyd算法

Dijkstra算法

单源点最短路径问题

Dijkstra算法主要用来解决单源点最短路径问题。

给定带权有向图G=（V,E)，其中每条边的权是非负数。另外，还给定V中的一个顶点，称为源。现在要计算从源到所有其他各顶点的最短路径长度，这里路径的长度是指路径上各边权之和。这个问题通常称为单源最短路径问题（Single-Source Shortest Paths)。

应用实例——计算机网络传输：怎样找到一种最经济的方式，从一台计算机向网上所有其它计算机发送一条消息。

思想

设置一个集合S存放已经找到最短路径的顶点，S的初始状态只包含源点v，对vi∈V-S，假设从源点v到vi的有向边为最短路径。以后每求得一条最短路径v, …, vk，就将vk加入集合S中，并将路径v, …, vk , vi与原来的假设相比较，取路径长度较小者为最短路径。重复上述过程，直到集合V中全部顶点加入到集合S中。

数据结构：
图的存储结构：带权的邻接矩阵。
数组distance[n]：每个distance[i]记录源点到各顶点的最小距离。

例：

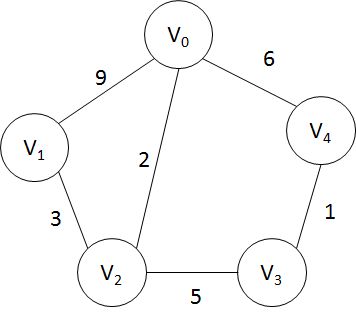
它的邻接矩阵：

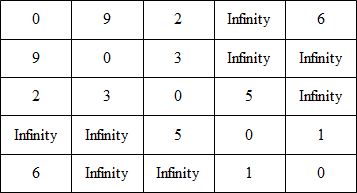
第一步：假设源点为V0，那么目前最短路径的顶点集合Q中就只有{V0}和无法到达顶点集合R中有{V1, V2, V3, V4}

第二步：初始化distance数组，就是下面这样

第三步：以distance数组中值为非Infinity的顶点为中转跳点，这一步就是V0，依照如果distance[V] + matrix[V][W] < distance[W]，那么distance[W] = distance[V] + matrix[V][W]的规则，distance数组就会变成下面这样，同时集合Q变成了{V0, V1, V2, V4}，集合R变成了{V3}

第四步：因为集合R中还有1个顶点，所以重复第三步的方法，然后变成以V1为中转跳点，但是以V1为中转顶点都不满足distance[V] + matrix[V][W] < distance[W]，所以没更新distance和两个集合

第五步：因为集合R中还有1个顶点，所以重复第三步的方法，此时变成以V2为中转跳点，然后发现V0到达V3的距离可以更新，因为2 + 3 < 9，所以distance更新，集合也更新。

之后同理，遍历完distance之后，输出

代码

function Dijkstra(matrix, start = 0) {
    const rows = matrix.length,//rows和cols一样，其实就是顶点个数
        cols = matrix[0].length;
 
    if(rows !== cols || start >= rows) return new Error("邻接矩阵错误或者源点错误");
 
    //初始化distance
    const distance = new Array(rows).fill(Infinity);
    distance[start] = 0;
 
    for(let i = 0; i < rows; i++) {
        //达到不了的顶点不能作为中转跳点
        if(distance[i] < Infinity) {
            for(let j = 0; j < cols; j++) {
                //比如通过比较distance[i] + matrix[i][j]和distance[j]的大小来决定是否更新distance[j]。
                if(matrix[i][j] + distance[i] < distance[j]) {
                    distance[j] = matrix[i][j] + distance[i];
                }
            }
            console.log(distance);
        }
    }
    return distance;
}
 
/**
 * 邻接矩阵
 * 值为顶点与顶点之间边的权值，0表示无自环，一个大数表示无边(比如10000)
 * */
const MAX_INTEGER = Infinity;//没有边或者有向图中无法到达
const MIN_INTEGER = 0;//没有自环
 
const matrix= [
    [MIN_INTEGER, 9, 2, MAX_INTEGER, 6],
    [9, MIN_INTEGER, 3, MAX_INTEGER, MAX_INTEGER],
    [2, 3, MIN_INTEGER, 5, MAX_INTEGER],
    [MAX_INTEGER, MAX_INTEGER, 5, MIN_INTEGER, 1],
    [6, MAX_INTEGER, MAX_INTEGER, 1, MIN_INTEGER]
];

Floyd算法

主要用于解决任意两点间最短路径问题的算法。

思想

对于从vi到vj的弧，进行n次试探：首先考虑路径vi,v0,vj是否存在，如果存在，则比较vi,vj和vi,v0,vj的路径长度，取较短者为从vi到vj的中间顶点的序号不大于0的最短路径。在路径上再增加一个顶点v1，依此类推，在经过n次比较后，最后求得的必是从顶点vi到顶点vj的最短路径。