FIRST集合
定义
可从α推导得到的串的首符号的集合,其中α是任意的文法符号串。
规则
计算文法符号 X 的 FIRST(X),不断运用以下规则直到没有新终结符号或 ε可以被加入为止 :
(1)如果 X 是一个终结符号,那么 FIRST(X) = X。
(2)如果 X 是一个非终结符号,且 X ->Y1 Y2 … Yk是一个产生式,其中 k≥1,那么如果对于某个i,a在 FIRST(Y1)、FIRST(Y2)… FIRST(Yi-1)中,就把a加入到 FIRST(X) 中。
(3)如果 X ->ε是一个产生式,那么将ε加入到 FIRST(X)中。
以上是书上的官方规则,不仅读起来很拗口,理解也很累。
下面看一下精简版的规则(从别人 @樱草书 那里看来的,感觉很棒,这里引用一下):
(1)如果X是终结符,则FIRST(X) = { X } 。
(2)如果X是非终结符,且有产生式形如X → a…,则FIRST( X ) = { a }。
(3) 如果X是非终结符,且有产生式形如X → ABCdEF…(A、B、C均属于非终结符且包含 ε,d为终结符),需要把FIRST( A )、FIRST( B )、FIRST( C )、FIRST( d )加入到 FIRST( X ) 中。
(4)如果X经过一步或多步推导出空字符ε,将ε加入FIRST( X )。
实践
记得,曾经有人说过:
只读,就会白给
下面以这个文法为例讲解一波,会用精简版规则,更容易理解一些:
E -> T E'
E' -> + T E' | ε
T -> F T'
T' -> * F T' | ε
F -> ( E ) | id
- 1
- 2
- 3
- 4
- 5
- FIRST(E) = FIRST(T) 根据规则3,很容易理解,这里要注意的由于T不含ε,所以遍历到T就停止了,E’不会加入进来
- FIRST(E’) = FIRST(+) ∪ FIRST(ε)= { +, ε } 根据规则2和4,,很好理解
- FIRST(T) = FIRST(F) 根据规则3,和第一条推导过程一样
- FIRST(T’) = FIRST() ∪ FIRST(ε)= { , ε } 根据规则2和4,和第二条推导一样
- FIRST(F) = FIRST( ( ) ∪ FIRST(id)= { ( , id } 根据规则2
结果:
FIRST(E) = FIRST(T) = FIRST(F) = { ( , id }
FIRST(E') = FIRST(+) ∪ FIRST(ε)= { + , ε }
FIRST(E') = FIRST(*) ∪ FIRST(ε)= { * , ε }
- 1
- 2
- 3
FOLLOW集合
定义
对于非终结符号A,FOLLOW(A) 被定义为可能在某些句型中紧跟在A右边的终结符号集合。
规则
计算文法符号 X 的 FOLLOW(X) ,不断运用以下规则直到没有新终结符号可以被加入任意FOLLOW集合为止 :
(1)将$加入到FOLLOW(X)中,其中S是开始符号,而$是输出右端的结束标记。
(2)如果存在一个产生式S->αXβ,那么将集合FIRST(β)中除ε外的所有元素加入到FOLLOW(X)当中。
(3)如果存在一个产生式 S->αX , 或者S->αXβ且FIRST(β)中包含ε , 那么将集合FOLLOW(S)中的所有元素加入到集合FOLLOW(X)中。
实践
还是用之前的例子来做
E -> T E'
E' -> + T E' | ε
T -> F T'
T' -> * F T' | ε
F -> ( E ) | id
- 1
- 2
- 3
- 4
- 5
- FOLLOW(E) ,根据规则1,首先把$加入进来,根据规则2,可以得出 FOLLOW(E) = { ) , $ }
- FOLLOW(E’) = FOLLOW(E) = { ) , $ } 根据规则3
- FOLLOW(T) = FIRST(E’) ∪ FOLLOW(E) = { + , ) , $ } 根据规则2
- FOLLOW(T’) = FOLLOW(T) = { + , ) , $ } 根据规则3
- FOLLOW(F) = FOLLOW(T) ∪ FIRST(T’) = { * , + , ) , $ } 根据规则2和3
结果:
FOLLOW(E) = FOLLOW(E') = { ) , $ }
FOLLOW(T) = FOLLOW(T') = { + , ) , $ }
FOLLOW(F) = { * , + , ) , $ }
- 1
- 2
- 3
LL(1)文法
解释
LL(1) 中第一个“L”表示从左向右扫描输入,第二个“L”表示产生最左推导,而“1”表示在每一步中只需要向前看一个输入符号来决定语法分析动作。
定义
对于文法LL(1)文法G,当且仅当G的任意两个不同产生式 A -> α | β
(1)不存在终结符号a使得α和β都能推导出以a开头的串。
(2)α和β中最多只有一个可以推导出空串。
(3)如果 β=》ε ,那么α不能推导出任何以FOLLOW(A)中某个终结符号开头的串。
可能很多人看的云里雾里,解释一下:
(1)和(2)意思是α和β的FIRST集合相交。(3)是指如果FIRST(α)中有 ε,那么FIRST(β)和FOLLOW(A)是不相交的集合,反之一样。
预测分析表的构建
方法:
对于文法G的每个产生式 A->α ,进行如下处理
(1)对于FIRST(α)中每个终结符号a,将 A->α 加入到 M[A,a] 中。
(2)如果 ε在FIRST(α)中,那么对于FOLLOW(A)中每个终结符号b,将 A->α 加入到 M[A,b] 中。如果 ε在FIRST(α),且$在FOLLOW(A)中,也将 A->α 加入到 M[A,$] 中。
还是以之前的例子示例
E -> T E'
E' -> + T E' | ε
T -> F T'
T' -> * F T' | ε
F -> ( E ) | id
- 1
- 2
- 3
- 4
- 5
1.先求FIRST和FOLLOW集合:
FIRST(E) = FIRST(T) = FIRST(F) = { ( , id }
FIRST(E') = FIRST(+) ∪ FIRST(ε)= { + , ε }
FIRST(T') = FIRST(*) ∪ FIRST(ε)= { * , ε }
FOLLOW(E) = FOLLOW(E') = { ) , $ }
FOLLOW(T) = FOLLOW(T') = { + , ) , $ }
FOLLOW(F) = { * , + , ) , $ }
- 1
- 2
- 3
- 4
- 5
- 6
2.然后构建一个这样的表

3.然后依次填入非终结符号
4.按照规则1填写其余内容

5.按照规则2填写内容
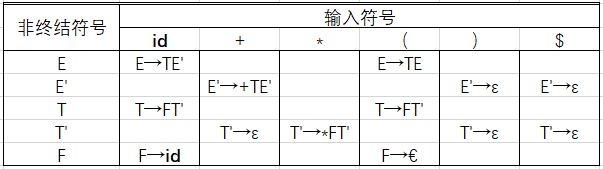
至此整个构建全部完成