基于R语言的线性回归模型诊断

一、线性回归模型假设条件

我们接着上篇文章《R语言下的线性回归模型》开始讲解线性模型诊断方面的操作。我们说过，线性模型的参数估计采用了最小二乘法的思想，但基于该思想是有前提假设的：

1）正态性假设：随机误差项服从均值为0，标准差为sigma的正态分布；

2）独立性：因变量y之间相互独立，即互不影响；

3）线性关系：因变量与自变量之间必须满足线性相关；

4）同方差性：随机误差项满足方差齐性；

只有线性模型满足以上几个假设条件，通过最小二乘法得到的结果才可能比较准确。

首先看一下多元线性模型的参数估计：

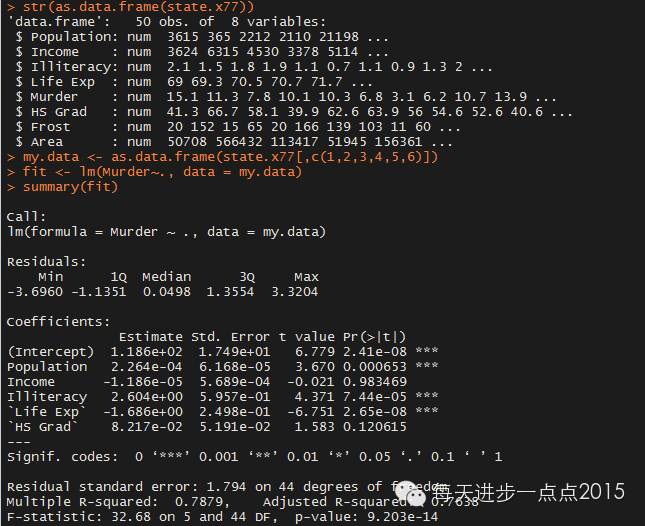
该模型除了Income和HS Grad变量没有通过显著性检验以外，剩余变量都是显著的，并且模型也通过检验，5个自变量解释了79%的因变量，似乎模型还能说的过去。接下来就对该模型做进一步的验证。

1、模型残差的正态性假设

正态性检验可以使用《定性与定量的单变量正态性检验》中自定义函数norm.test。

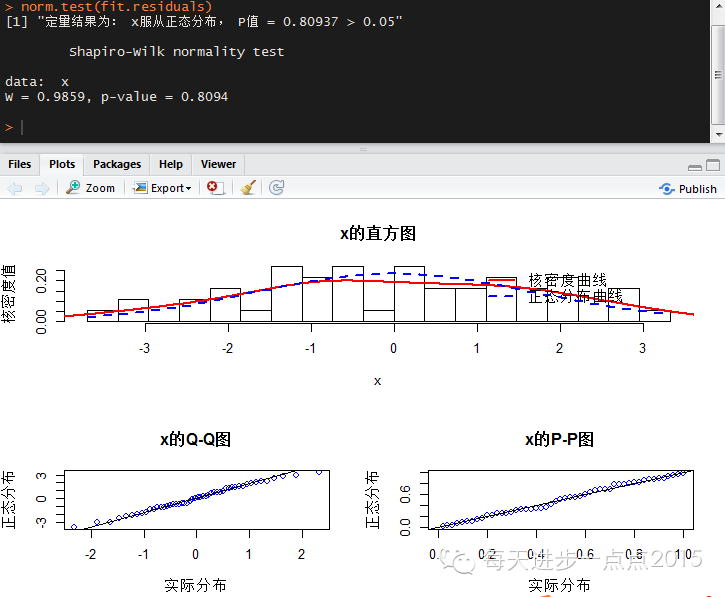
通过定性与定量的结果显示，模型的误差项满足正态性的假设。如果误差项不满足正态性检验，那么可以考虑对因变量采取Box-Cox转换（由于误差项是随机变量，因变量也是随机变量，如果误差项不满足正态性假设，也就意味着因变量也不满足正态性假设）。

关于Box-Cox转换可以使用car包中的powerTransform()函数。常见的转换形式可见如下表格：

从上图发现，需要变换的参数估计值为0.6，比较接近常见变换中的0.5，所以可以考虑将因变量Y变换为Y的开根号。但这里没有不建议这样操作，因为模型中的误差项已经服从正态分布了。

有关norm.test自定义函数的脚本可以到此处下载：

http://yunpan.cn/cH7dXVnCPRqKs 访问密码 f11e

2、独立性假设

对于截面数据，检验个体间是否相互独立，一般通过收集到的数据本身进行验证，无法直接定量得出。例如不同用户的购买习惯、网页浏览情况等。在本例中可以认为美国各洲之间的谋杀率是相互独立的。对于时间序列数据，检验观察间是否相互独立，可以考虑使用杜宾-瓦特森检验（D-W检验）。该检验可以使用car包中的durbinWatsonTest函数实现。为了使用该函数，我们不妨也使用一下该函数，检验观测检的独立性：

检验结果显示，P值大于0.05，接受独立的原假设，即序列间不存在自相关性。

3、线性关系

可以绘制因变量与各个自变量的散点图，确定两者之间是否存在明显的线性关系。如果不存在线性关系，可以考虑变量变换（如对数变换、指数变换、多项式变换等），实现因变量与自变量的线性关系。

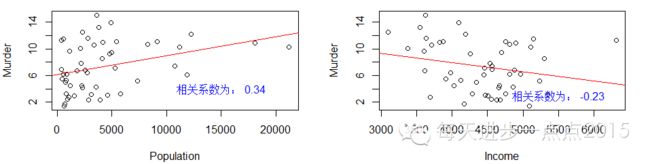
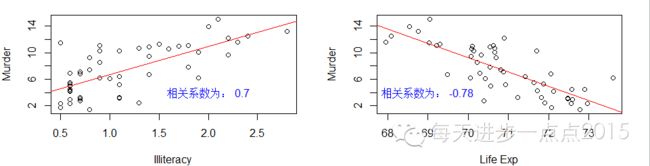
下面对因变量和自变量分别绘制散点图，以显示变量之间是否存在线性关系：

脚本如下：

#谋杀率与人口数的散点图

opar <- par(no.readonly = TRUE)

par(mfrow =c(1,2))

plot(my.data$Population, my.data$Murder,

xlab = 'Population', ylab = 'Murder')

abline(lm(my.data$Murder~my.data$Population), col = 'red')

text(15000,4,paste('相关系数为：',

round(cor(my.data$Population, my.data$Murder),2)),

col = 'blue')

#谋杀率与收入的散点图

plot(my.data$Income, my.data$Murder,

xlab = 'Income', ylab = 'Murder')

abline(lm(my.data$Murder~my.data$Income), col = 'red')

text(5500,3,paste('相关系数为：',

round(cor(my.data$Income, my.data$Murder),2)),

col = 'blue')

#谋杀率与文盲率的散点图

plot(my.data$Illiteracy, my.data$Murder,

xlab = 'Illiteracy', ylab = 'Murder')

abline(lm(my.data$Murder~my.data$Illiteracy), col = 'red')

text(2,4,paste('相关系数为：',

round(cor(my.data$Illiteracy, my.data$Murder),2)),

col = 'blue')

#谋杀率与寿命的散点图

plot(my.data[,'Life Exp'], my.data$Murder,

xlab = 'Life Exp', ylab = 'Murder')

abline(lm(my.data$Murder~my.data[,'Life Exp']), col = 'red')

text(69,4,paste('相关系数为：',

round(cor(my.data[,'Life Exp'], my.data$Murder),2)),

col = 'blue')

#谋杀率与高中毕业率的散点图

plot(my.data[,'HS Grad'], my.data$Murder,

xlab = 'HS Grad', ylab = 'Murder')

abline(lm(my.data$Murder~my.data[,'HS Grad']), col = 'red')

text(43,4,paste('相关系数为：',

round(cor(my.data[,'HS Grad'], my.data$Murder),2)),

col = 'blue')

plot(fit,which = 1)

par(opar)

从结果中可以得知只有各洲的文盲率、寿命与谋杀率存在较高的线性相关性。并且文盲率越高，谋杀率越高；老龄化越严重谋杀率越低。其他变量与谋杀率的相关性就显得不明显了。在“残差拟合值”散点图中明显存在一条非线性的曲线，说明某些变量与因变量之间不存在线性关系。

关于因变量与自变量的线性性假设，还可以通过成分残差图来判断各个自变量与因变量之间是否存在线性相关。该图的实现可运用car包的crPlots()函数。

library(car)

crPlots(fit)

可见该函数返回的线性相关性检验可视化图与上图中的散点图结论基本一致。

4、同方差性

如果模型的残差项不满足方差齐性的话，最小二乘估计将产生严重的错误，如参数估计量的方差不具有最小方差性，那么估计与预测的精度降低。

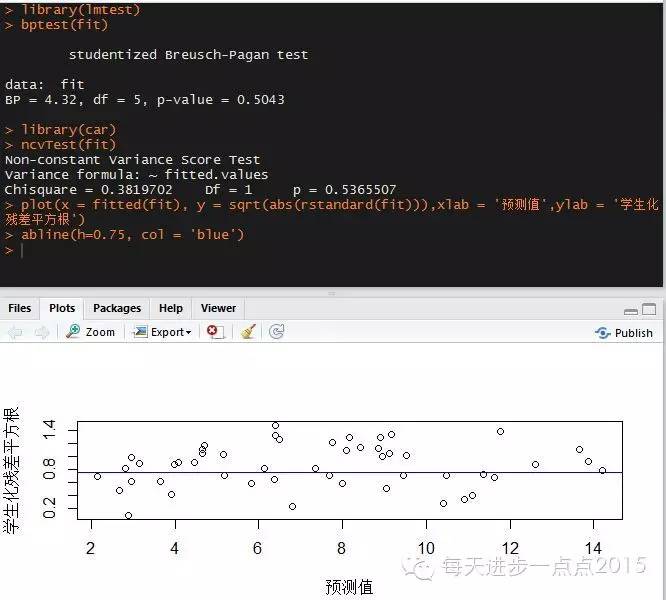
对于模型误差项方差齐性的检验可以使用扩展包lmtest中的bptest()函数。或者利用car包中的ncv.test()函数。

library(lmtest)

bptest(fit)

library(car)

ncvTest(fit)

不论从定性（位置尺度图中的散点随机分布在水平线0.75附近）和定量（P值均大于0.05）的角度，都可以说明模型的误差项符合方差齐性的假设。如果误差项不满足方差齐性的假设，也可以考虑Box-Cox变换，使模型的误差项满足方差齐性。

二、线性回归模型诊断

自变量之间如果有较强的相关关系，就很难求得较为理想的回归方程；若个别观测点与多数观测点偏离很远或因过失误差(如抄写或输入错误所致)，它们也会对回归方程的质量产生极坏的影响。对这两面的问题进行监测和分析的方法，称为回归诊断。前者属于共线性诊断问题；后者属于异常点诊断问题。

1、共线性诊断

多重共线性是指线性回归模型中的解释变量之间由于存在精确相关关系或高度相关关系而使模型估计失真或难以估计准确。一般通过方差膨胀因子（VIF）检验模型中的自变量间是否存在多重共线性。car包中的vif()函数可以实现检验。

一般方差膨胀因子大于4就可能存在多重共线性问题。从上图中，没有一个变量的方差膨胀因子大于4，可以认为变量间不存在多重共线性。除了vif函数外，还可以使用R自带的kappa()函数检验模型中变量的多重共线性。

kappa(cor(my.data[,c('Population', 'Income',

'Illiteracy', 'Life Exp', 'HS Grad')]))

[1] 8.75853

一般k<100时，则认为多重共线性可能性很小，100<= k <= 1000时，认为存在中等程度或较强的多重共线性，而k>1000时，认为存在严重的多重共线性。从结果中也说明这5个变量间不存在多重共线性。

2、异常点诊断

有关异常点诊断，《统计建模与R语言》中提到了帽子矩阵对角元素检验法、DFFITS准则、Cook统计量和COVRATIO准则。

帽子矩阵对角元素检验法

如果帽子矩阵对角元素满足如下条件，则认为第i组样本影响较大，可以结合其他准则，考虑是否将其剔除。

其中X为自变量值矩阵，p为自变量个数，n为样本量。

R中hatvalues()函数可以直接求得帽子矩阵的对角元素。

DFFITS准则

在满足以上条件时，可以认为第i个样本影响比较大，需要引起注意。R中dffits()函数可以计算得到D统计量。

Cook统计量

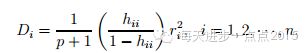
该统计量的计算可以使用cooks.distance()函数求得。一般来说，Cook统计量越大，说明该点越可能为异常点。但该方法的缺点是无法界定Cook统计量多大才算大，这需要视具体情况而定。

COVRATIO准则

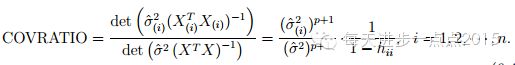
有关COVRATIO值的计算可以直接使用covratio()函数得到。判定原则是：COVRATIO值离1越远，则认为样本对模型的的影响越大。

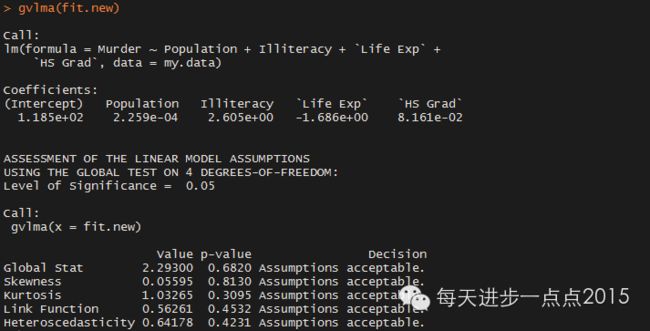
到此，基本完成了本文的两个任务，即模型的假设检验和模型的诊断，中间使用到了很多的函数来实现模型的检验。R中提供了一个非常便捷的函数可以直接进行模型的假设检验，该函数是gvlma包中的gvlma函数。

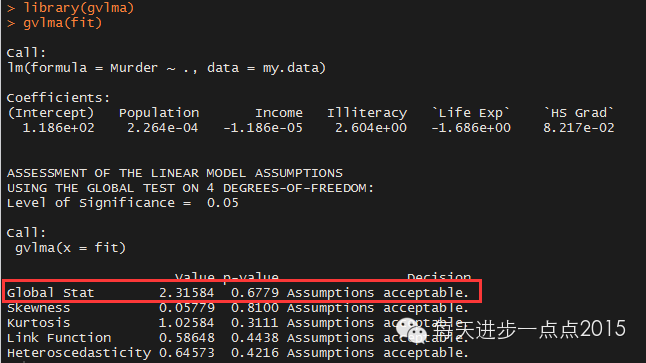
从上图中的红框内容显示，数据满足OLS回归模型的所有统计假设。如果“全局统计量”被拒绝，即认为模型不满足统计假设时，可以回到前面的检验过程进行一一验证并修正。

最后再讲解一下多元线性回归模型中逐步回归的过程，该过程分向前回归、向后回归和向前向后回归。

向前回归指原始模型不包含任何自变量，在该回归过程中一一向模型添加满足条件的自变量。

向后回归指原始模型包含所有自变量，在该过程中一一删除某些不满足条件的自变量。

向前向后回归则是同时考虑向前回归和向后回归，使模型在选择变量时有出有进。

R中step()函数就是用于实现多元线性模型的逐步回归过程，指定step()函数中direction参数，可以实现向前、向后和向前向后逐步回归。

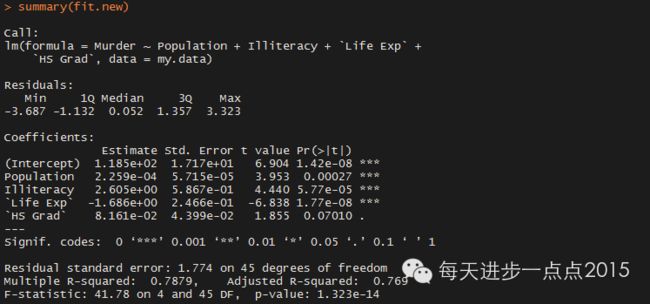
fit.new <- step(fit,direction = 'both')

summary(fit.new)

gvlma(fit.new)

可见新模型在满足OLS假设条件前提下，模型的系数也通过了显著性检验，模型有进一步的提升。

参考文献

http://blog.csdn.net/yujunbeta/article/details/8169475

R语言实战

统计建模与R语言

总结：文中涉及到的R包和函数

stats包

lm()

plot()

abline()

kappa()

hatvalues()

dffits()

cooks.distance()

covratio()

step()

car包

powerTransform()

durbinWatsonTest()

crPlots()

ncvTest()

lmtest包

bptest()

vif()

gvlma包

gvlma()