吴恩达深度学习课后作业汇总及遇到的问题

         近期正在学习吴恩达老师的深度学习课程，相关的博文正在逐步更新，之所以没有写完之后再发布是为了再学习过程中能和更多的人交流，希望能够找到一群跟我进度差不多的小伙伴共同交流进步~~所以欢迎大家积极留言~

        本文主要是分享了一位博主整理的课后作业，以及自己在做作业过程中遇到的一些疑问以及解决办法。

作业：

         网易云课堂上没有提供作业的下载入口，在CSDN上找了很多作业的分享，下面这个博主总结的还是比较全面且细致的：

https://blog.csdn.net/u013733326/article/details/79827273

         上面的博客中写的是博主翻译过来的，以及一些答案，英文版的原始作业下载链接如下：

https://download.csdn.net/download/m0_37704205/11615539

遇到的问题：

第一课第二周：

1.在深度学习课程作业中有这样一段话：

A trick when you want to flatten a matrix X of shape (a,b,c,d) to a matrix X_flatten of shape (b * c *d, a) is to use:

X_flatten = X.reshape(-1,X.shape[0])

但是后面实际应用的代码与上述语句还是有一些不同的：

train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0],-1).T

可见降维操作输入的两个参数的位置有点不同，而且trick中降维之后也不需要进行转置，于是我试着用trick中的方式实现降维操作，相关语句如下：

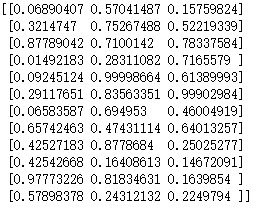
train_set_x_flatten = train_set_x_orig.reshape(-1,train_set_x_orig.shape[0])

发现输出的目标维度和示例代码中的没有差别，都是（12288,209），那为什么示例代码中和提示中的示例不一样呢？用trick中的语句到底行不行呢？后来检测一下将为后的前5个数据输出，发现确实不一样：

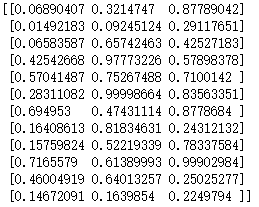
而正确输出则应该是这样：

后来我在 jupyter 中写了一个小的例子验证了一下才知道了原因：

首先我们要知道reshape函数中输入参数-1 的含义：根据另一个维度自动计算出相应的参数，比如一共有500个参数，如果你输入了一个参数为5，那么-1代表的便是500/5=100。

因此之前那两种不同的写法的输出参数的维度是相同的，导致数据不同的原因只能是对这些数据的组合方式不同，于是我在jupyter中写了如下代码：

import numpy as np
a = np.random.random((3,2,2,3))#随机生成一个数组
print(a)
a1 = a.reshape(a.shape[0],-1).T
print(a1)
a2 = a.reshape(-1,a.shape[0])
print(a2)

输出结果如下：

原数组：

数组a1:

数组a2:

通过观察可以发现，维度都是相同的，但是数据的排列方式不同。哪一种方式才是我们想要的呢？我们的目的是重新排列这些数组，使得每一列中所有的数据都是同一副图片中的数据，所以我们可以看到带转置的那种方式是正确的。

第一课第三周：

1.如何理解np.random.randn()？

在使用numpy时，经常会用到随机数生成器，在吴老师的作业中便出现了这样一行代码：

np.random.seed(1) # set a seed so that the results are consistent

我查阅的相关资料，网上说这个方法的作用是利用随机数种子，使每次生成的随机数相同，这句话不是很好理解；也有一些说法说这个只是一次有效，对后面的不会有影响，也有的人说对后面一直有效，于是我做了以下的实验进行验证：

首先初始化一个随机数种子，然后生成一个10个数的序列，然后再初始化一次，重新生成两个5个数的序列

np.random.seed(0)
print(np.random.randn(1,10))
np.random.seed(0)
print(np.random.randn(1,5))
print(np.random.randn(1,5))

 生成的结果如下：

    可见这两次运行的结果都是一样的。这边可以解释“使每次生成的随机数相同”这句话，而且我们可以看到，后面的用两行代码分别生成一些随机数，这些数和一次性生成的10个是相同的，所以说这个种子只是确定了随机数开始的位置，是会一直影响后面随机数生成的。

第一课第四周：

  1.参数初始化的问题。

在构建多层神经网络时，按照吴恩达老师的课后作业中的代码，对权重矩阵参数W的初始化方法为：

np.random.seed(3)
parameters['W' + str(l)] = np.random.randn(layer_dims[l],layer_dims[l-1]) * 0.01

即设置好随机数种子之后，将W进行随即初始化，然后乘上0.01。这种方法在运行时出现了一个问题：就是其代价函数停在0.64左右，似乎是陷入了一个局部最小值，我尝试了改变乘的系数，改变迭代次数和学习速率发现效果都不是很好。准确率甚至达不到0.5。后来参考了很多答案发现他们初始化时乘的不是0.01，而是一个根据维度变化的值：

parameters['W' + str(l)] = np.random.randn(layer_dims[l],layer_dims[l-1]) * np.sqrt(1.0/layer_dims[l-1])

然后在这位博主的博客下面找到了答案：

https://blog.csdn.net/cherry_yu08/article/details/79116862

原因是不同的激活函数的初始化方法是不同的，（吴老师的视频当时只是说还有其他的方法，并没有详细的解释）例如：

1.激活函数为tanh时，令W的方差为 ：

w[l] = np.random.randn(n[l],n[l-1])*np.sqrt(1/n[l-1])

2.激活函数是ReLU，权重w的初始化一般令其方差为  ：

w[l] = np.random.randn(n[l],n[l-1])*np.sqrt(2/n[l-1]) 

3.Yoshua Bengio提出一种初始化w的方法，令其方差为 ：

w[l] = np.random.randn(n[l],n[l-1])*np.sqrt(2/(n[l-1]+n[l])) 

由于文中的激活函数用的是relu函数，所以我按照上图中的激活函数进行初始化之后，发现代价函数变得非常小了，而且准确度也比作业答案中提高了0.02个点。看来不同参数的初始化方式对最终的结果影响还是很大的。