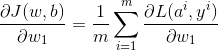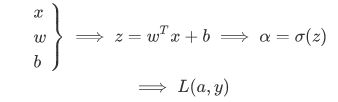吴恩达深度学习系列笔记：第一课 神经网络和深度学习

第二周 神经网络基础

1.logistic回归

       logistic回归是一个用于二分分类的算法，即输入一幅图像（64x64x3=12288），输出1或者0，将图像中的特征全部提取出来，形成一个[12288,1]的特征矩阵，若是M个样本，则M_train = [12288,m]，Y=[y1,y2...ym].输入参数X的维度为[12288,m]，参数w的维度同为[12288,1]，b为一个实数，则输出

                                                                              

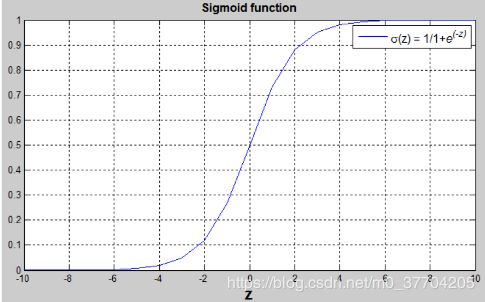
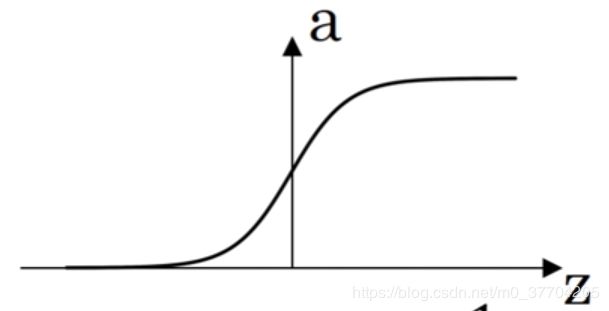
由于输出要控制在0-1之间，因此要通过激活函数将输出变换一下。logistic回归常通过sigmoid函数进行变换，其函数图像如下：

                                                              

数学表达式为

 

 

                                                                          

符号约定：在神经网络中，我们常会把w和b分开，b在这里对应着一个拦截器，有的约定法则将b也写入参数矩阵w中。

2.代价函数

        我们可以这样定义一个损失函数：
                                                                        

        这个函数比较容易理解，但是当使用在logistic回归过程中，在学习这些参数时，之后讨论的优化问题会变成非凸的，容易得到一些局部最优解，梯度下降法可能找不到局部最优值。在logistic回归中，我们常定义以下函数为损失函数，便可以使得损失函数变为一个凸函数：

                                                        

        当y=1时，，如果我们想让损失函数尽可能的小，则需要尽可能的大，但是被sigmoid函数限制在0-1之间，所以最终会趋向于1。同理我们可以推出当y=0时，想让损失函数尽可能的小，需要让尽可能的小，所以最终也会趋向于0。

       损失函数是衡量单个样本的输出值和真实值之间的差距，要衡量所有样本输出值和真实值的差距，我们需要定义一个代价函数：

                                     

可以看出，代价函数只是对所有样本的损失函数进行了简单的平均化处理。

       代价函数推导：

已知：

                                                       

我们设定y帽为给定样本x条件下y=1的概率。

                                                                     

则给定样本x条件下y=0的概率为：

                                                                     

将两式合在一起可以得到：

                                                                    

然后取对数即可获得：

                                                          

由于训练过程需要最小化损失函数，所以前面要加一个负号。

多样本损失函数是假设各样本在独立同分布的条件下进行极大思然估计，使得损失函数达到最小。

3.梯度下降法

        用来训练w和b，来使代价函数达到最小。首先初始化w,b,梯度下降法便是使代价函数上面的点每次都向着它周围最陡的方向走一步，直到到达最优解。

        首先我们以一阶的代价函数为例，其函数图像如下图所示。

                                                   

每次都按照以下公式进行参数更新：

                                                                    

容易看出，当导数为负数时，w会增大，随之J(w)的值会逐渐变小。反之，如果导数为正，w会逐渐变小，导致J(w)的值会逐渐增大。由于实际使用时J(w)有w和b两个参数，所以我们还需要用相同的方式更新b:

                                                                     

4.logistic回归中梯度下降法的应用

        将前文中求得的logistic回归所用到的公式整理如下：

                                                                 

                                                                

                                             

其中a是logistic回归的输出，y是实际的值。

假设logistic回归中有x1,x2两个输入参数，我们需要更新参数w和b来使损失函数逐渐变小：

                                   

由于链式法则，要求得最终损失函数L的偏导，我们首先要求得a的导数：

                                                                     

然后可以求出a对z的偏导：

                                                             

最终容易求得

                                                                 

在实际编程中我们常用dz来表示L对z的偏导数。

之后便容易求得参数

                                                

                                                 

                                                                       

然后根据下式进行更新即可：

                                                                        

                                                                        

                                                                            

5.多样本的梯度下降法

    多样本的梯度下降法就是将单样本对某一参数的梯度求平均，以w1为例：

                                                         

梯度下降法迭代一步参数更新代码如下：

import numpy as np
J=0  
dw1=0
dw2=0
db=0
for i in range(m):
    z(i)=w'*x(i)+b
    a(i)=sigmoid(z(i))
    J = J-[y(i)*loga(i)+(1-y(i)*log(1-a(i)]
    dz(i) =a(i)-y(i)
    dw1 = dw1+x1(i)+dz(i)
    dw2 = dw2+x2(i)+dz(i) 
    db = db+dz(i)
J=J/m
dw1 = dw1/m #全局的累加，所以没有标号
dw2 = dw2/m
db = db/m
w1:=w1-alpha*dw1
w2:=w2-alpha*dw2
b:=b-alpha*db

        可见如果w的数目特别多的时候，计算起来很不方便，如果使用for循环则会大大的降低程序的效率，所以我们要进行向量化处理。

6.向量化

      向量化处理常用于消除代码中显式的for循环，提高代码效率。对于一个100k大小的数组，使用向量化进行处理比for循环快近300倍。

       假设有m个样本，每个样本有10000个特征，则X就是一个10000*m大小的矩阵，同样w是一个10000*1的矩阵,b是一个mx1的矩阵，根据之前得到的式子容易推出

                                                                                

则第5节中的代码去掉for循环之后为：

import numpy as np
Z = np.dot(w.T,x)+b #[1,1000]*[1000,60]+[1,60]
A = sigmoid(Z)  #[1,60]
dZ = A-Y        #[1,60]
dW = X*dZ.T/m   #[1000,1]
db = np.sum(dZ)/m #1
W:=W-alpha*dW
b:=b-alpha*db

7.python使用时的一些编程技巧

1.生成矩阵时一定要声明矩阵的大小,例如：

import numpy as np
a = np.random.randn(5)#不规范的初始化方式
a = np.random.randn(5,1)#初始化为5X1的矩阵

第三周 浅层神经网络

1.神经网络概览

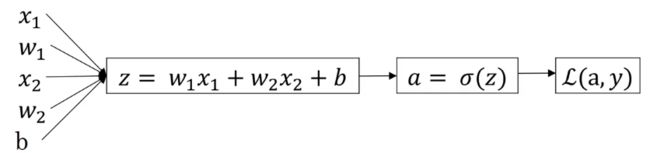
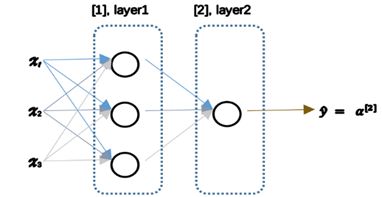
       本周的任务是实现一个神经网络，我们首先把前面学到的公式和常用的神经网络模型结合起来，最简单常见的一个神经网络模型如下图所示：

公式：

      首先第一个神经元完成了两部分操作：计算出Z并且使用sigmoid函数进行激活得到a。然后用a来表示y帽。最后就可以计算损失函数L。

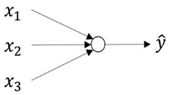
      在神经网络中，我们可以将许多个sigmoid单元堆叠起来形成一个大的神经网络:

在神经网络的第一层中的三个节点分别进行的操作如下：

                                                                      

        这里的上标【1】表示的是第一层网络，下标1,2,3表示的是某一层的第几个参数 ，算出来之后，再把这些作为新的输入参数，然后再赋予一个权重矩阵,然后在第2层中再一次计算.然后输出,即最终输出。简单的说，就是每一层都要单独输入一个权重矩阵。

例：共有600个训练样本，每个样本有10000个特征，则输入矩阵X的维度为(10000,600)，如果训练的网络模型如上所示，则对应的的维度都为(10000,1)，（PS：单个神经元的600个样本的w都是相同的，即使是600个样本，也应该只有一个w）。b的维度可以直接通过广播来确定，也可以人为设置为（10000,1）。所以第一层神经网络可以获得这三个参数，分别对应着第一个神经元对所有第二层的维度为（3,1），也为（3,1）。

2.激活函数

1.sigmoid函数

函数表达式为：

                                                           

图像如下：

2.双曲正切函数

函数表达式为：

                                                     

图像如下：

        可见双曲正切函数是相当于对sigmoid函数进行上下平移，这样使得输出的平均值可以为0，类似于数据中心化的效果，可以使下一层的计算更加方便。

        以上说的这两种激活函数也有一个比较明显的缺陷：当Z特别大或者特别小的时候，该点的斜率就会变得比较小，这样一来应用梯度下降法的效果就不显著，下面这一种激活函数（又叫线性修正单元）ReLU可以避免这个问题。

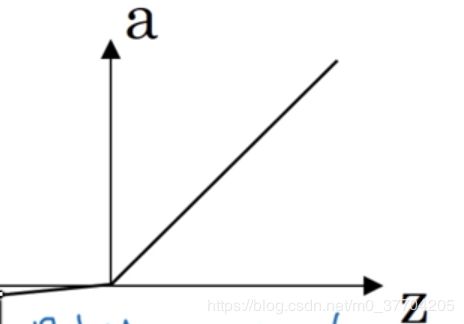
3.线性修正单元（RELU）

    该函数的表达式如下：

                                                                   

当Z大于零的时候，函数的导数一直为一，小于零则为零。这个函数一般是隐藏层节点的默认激活函数。

4.leaking ReLU

      该函数的表达式如下：

                                                                 

       图像：

3.为什么要用非线性激活函数？

如果使用线性激活函数，则模型的复杂度和直接计算输入参数不相上下，不如直接去掉隐藏层。只有当遇到机器学习中的回归函数时才会使用线性函数进行计算。 

4.激活函数的导数

sigmoid函数：

                                                                     

双曲正切函数导数：

                                                   

ReLU函数：

                                                                 

                                                               

Leaky ReLU函数:

                                                            

                                                            

5.神经网络的梯度下降法（反向传播）

        本节主要是进一步的解释了梯度下降法在神经网络中的应用，与之前梯度下降法那一节的课程有一些重复的地方，可以当作是重新温习一下。

以一个2层的神经网络为例，单个样本的特征数目，第一层节点个数为，第二层节点个数为。

相关参数：的维度分别为。z=w^{T}x+b，a为经过激活后的输出。

如之前所介绍，正向传播需要以下四个公式：

                                                                   

                                                                  

                                                                  

                                                                 

反向传播需要的公式稍微多一点，推导过程可以参照之前对梯度下降法的介绍：

                                                                            

                                                                           

                                                

                                         应注意这里用的是激活函数的导数

                                                                           

                                                  

第四周 深层神经网络

1.深层神经网络的概念

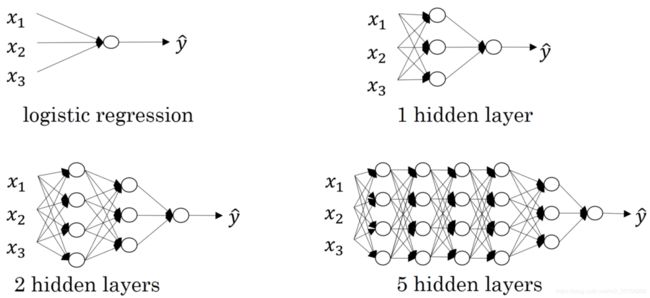
线性回归、单隐层神经网络（双层神经网络）、双隐层神经网络和5隐层神经网络的结构图如下所示：

符号约定：

L是神经网络层数；为神经网络某一层的节点数,n0为输入层，为某一层的激活函数

2.核对矩阵的维数

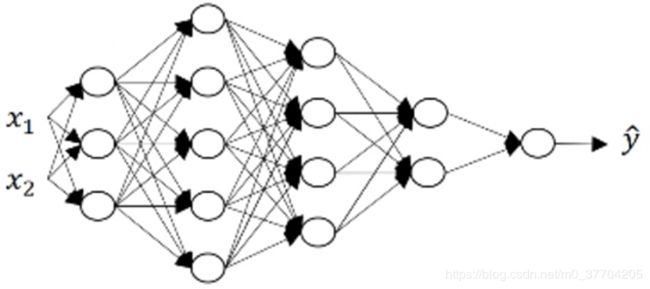
       以一个5层神经网络为例，其示意图如下所示：

        遵循上一节的符号约定，加上输入参数x,该神经网络的层数分别表示为,下面举一个例子来确认一下神经网络的层数：

        假设共有600(m=600)个输入样本，每个样本分别有1000个特征（即）,则向量化后X的维数为[1000,600],即,则神经网络第一层参数的维度分别为：

            其中：

                                                                     自然  

同样的可以计算出第二层各参数的维度：

                                                            其中：

                   

                                                     同样  

通过这两层的例子，我们可以看出如下规律：

                    他们的导数维数也不变.

3.实现正向和反向传播

正向传播：输入，输出，缓存。

反向传播：输入，输出,

反向传播的公式如下：

                                                              应注意这里用的是激活函数的导数

                                                              

                                                

                                                               

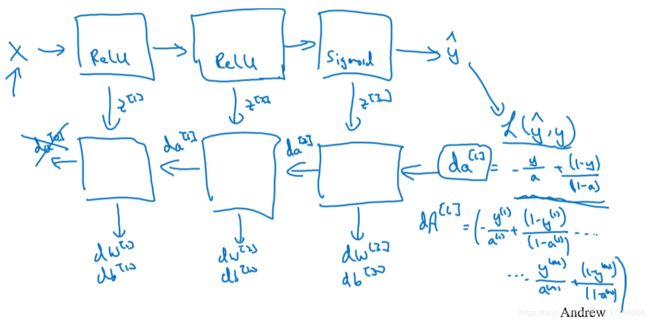
 一个深度神经网络的实现过程可以由下图来展示：

4.参数和超参数

超参数：能够控制学习参数的参数被称为超参数。例如在神经网络中，学习率、隐层的数量、节点的数量、迭代的次数、激活函数的选择等等这些参数都可以控制W和B的变化，因此这些参数被称为超参数。

可以通过查看代价函数的收敛情况来改变学习率这个超参数。