泊松分布分布与Python图解
import numpy as np
import matplotlib.pyplot as plt
from numpy import power
from scipy.special import comb
相关知识
Bernoulli Experiment (伯努利试验)
对于一个试验(事件),如果重复发生的概率是独立的(互补影响),那么它是独立试验。特别的,如果这个试验只存在两种结果,则称其为伯努利试验。
Binomial Distribution (二项式分布)
对于重复 n n n次的伯努利试验,我们可以计算成功 k k k次的概率:
P k = C n k p k ( 1 − p ) n − k = n ! ( n − k ) ! k ! ⋅ p k ( 1 − p ) n − k P_{k}=C_{n}^{k} p^{k}(1-p)^{n-k}=\frac{n !}{(n-k) ! k !} \cdot p^{k}(1-p)^{n-k} Pk=Cnkpk(1−p)n−k=(n−k)!k!n!⋅pk(1−p)n−k
def BinomialDist(n, k, p=.5):
return comb(n, k) * power(p, k) * power(1-p, n-k)
e.g. 假设我们抛一枚硬币,总共抛10次,求10次都是正面的概率?
解: P 10 = 0. 5 10 P_{10} = 0.5^{10} P10=0.510
验证一下我们的函数:
BinomialDist(10, 10) == power(0.5, 10)
True
e.g. 假设我们抛一枚硬币,总共抛10次,分别求 k = 0 , 1 , 2 , . . . , 10 k=0,1,2,...,10 k=0,1,2,...,10次是正面的概率?
ks = np.linspace(0, 10, 11) #ks=0,1,2,...,10
Plst = BinomialDist(10, ks)
plt.plot(Plst, '.')
plt.title(r'$P(X=k),\ X \sim B(10,0.5)$')
plt.show()
从上图可以看出, k = 5 k=5 k=5时候最大,这符合我们的预期:抛10次硬币,正面朝上的次数最有可能为5。即随机变量 ξ ∼ B ( 10 , 0.5 ) \xi \sim B(10, 0.5) ξ∼B(10,0.5), E ( ξ ) = n p = 5 E(\xi)=np=5 E(ξ)=np=5。
简单证明一下 E ( ξ ) = n p E(\xi)=np E(ξ)=np:
-
预备公式: k c n k = n c n − 1 k − 1 k c_{n}^{k}=n c_{n-1}^{k-1} kcnk=ncn−1k−1
-
离散型随机变量 ξ \xi ξ的期望: E ( ξ ) = ∑ i n ( x i ⋅ p ( x i ) ) E(\xi)=\sum_i^n(x_i\cdot p(x_i)) E(ξ)=∑in(xi⋅p(xi))
-
这里 x i = k = 0 , 1 , . . . , n x_i = k = 0,1,...,n xi=k=0,1,...,n,而 p ( x i ) = p ( k ) = C n k p k ( 1 − p ) n − k p(x_i)=p(k)=C_{n}^{k} p^{k}(1-p)^{n-k} p(xi)=p(k)=Cnkpk(1−p)n−k
E ( ξ ) = 0 × c n 0 p 0 q n + 1 × c n 1 p 1 q n − 1 + 2 × c n 2 p 2 q n − 2 … + n c n n p 0 q n = n p ( c n − 1 0 p 0 q n − 1 + c n − 1 1 p 0 q n − 2 + c n − 1 2 p 0 q n − 2 … + c n − 1 n − 1 p n − 1 q 0 ) = n p ( p + q ) n − 1 = n p \begin{aligned}E(\xi) &= 0 \times c_{n}^{0} p^{0} q^{n}+1 \times c_{n}^{1} p^{1} q^{n-1}+ 2 \times c_{n}^{2} p^{2} q^{n-2}\ldots+n c_{n}^{n} p^{0} q^{n}\\ &= n p\left(c_{n-1}^{0} p^{0} q^{n-1}+c_{n-1}^{1} p^{0} q^{n-2}+c_{n-1}^{2} p^{0} q^{n-2} \ldots+c_{n-1}^{n-1} p^{n-1} q^{0}\right)\\ &= n p(p+q)^{n-1}\\ &= n p\end{aligned} E(ξ)=0×cn0p0qn+1×cn1p1qn−1+2×cn2p2qn−2…+ncnnp0qn=np(cn−10p0qn−1+cn−11p0qn−2+cn−12p0qn−2…+cn−1n−1pn−1q0)=np(p+q)n−1=np
计算一下 E ( ξ ) = ∑ i n ( x i ⋅ p ( x i ) ) E(\xi)=\sum_i^n(x_i\cdot p(x_i)) E(ξ)=∑in(xi⋅p(xi)),ks相当于 x i x_i xi,Plst相当于 p ( x i ) p(x_i) p(xi)
print('mean =', (ks*Plst).sum())
print('mean =', 10*0.5)
mean = 5.0
mean = 5.0
其他证明方法和方差( D ( ξ ) = n p q D(\xi)=npq D(ξ)=npq)可以参考二项分布的期望和方差的详细证明。
D ( X ) = E ( X 2 ) − E 2 ( X ) = ∑ k = 0 ∞ k 2 ⋅ λ k k ! e − λ − λ 2 = λ e − λ ∑ k = 1 ∞ k λ k − 1 ( k − 1 ) ! − λ 2 = λ e − λ [ ∑ k = 2 ∞ λ k − 1 ( k − 2 ) ! + ∑ k = 1 ∞ λ k − 1 ( k − 1 ) ! ] − λ 2 = λ e − λ [ λ e λ + e λ ] − λ 2 = λ \begin{array}{l} D(X)=E\left(X^{2}\right)-E^{2}(X)=\sum_{k=0}^{\infty} k^{2} \cdot \frac{\lambda^{k}}{k !} e^{-\lambda}-\lambda^{2} \\ =\lambda e^{-\lambda} \sum_{k=1}^{\infty} \frac{k \lambda^{k-1}}{(k-1) !}-\lambda^{2}=\lambda e^{-\lambda}\left[\sum_{k=2}^{\infty} \frac{\lambda^{k-1}}{(k-2) !}+\sum_{k=1}^{\infty} \frac{\lambda^{k-1}}{(k-1) !}\right]-\lambda^{2} \\ =\lambda e^{-\lambda}\left[\lambda e^{\lambda}+e^{\lambda}\right]-\lambda^{2}=\lambda \end{array} D(X)=E(X2)−E2(X)=∑k=0∞k2⋅k!λke−λ−λ2=λe−λ∑k=1∞(k−1)!kλk−1−λ2=λe−λ[∑k=2∞(k−2)!λk−1+∑k=1∞(k−1)!λk−1]−λ2=λe−λ[λeλ+eλ]−λ2=λ
总结,如果随机变量 X = k X=k X=k的概率满足 P ( X = k ) = C n k p k ( 1 − p ) n − k P(X=k)=C_{n}^{k} p^{k}(1-p)^{n-k} P(X=k)=Cnkpk(1−p)n−k二项式分布,则 X ∼ B ( n , p ) X \sim B(n,p) X∼B(n,p)。
定义
二项式分布 P ( k ) = n ! ( n − k ) ! k ! ⋅ p k ( 1 − p ) n − k P\left(k\right)=\frac{n !}{(n-k) ! k !} \cdot p^{k}(1-p)^{n-k} P(k)=(n−k)!k!n!⋅pk(1−p)n−k要求 n n n必须为已知数,但是生活中很多事情是没法统计出或者不存在精确的总数,这些事情往往是在一段连续的时间内出现一定的次数,相互之间没有影响(随机发生),并且单次事件耗时和概率几乎可以忽略(只有出现或者未出现,类似二项式分布;任意时刻发生的概率几乎为0)。例如,某个医院一天/一小时/一周内来的病人数量;某个包子店一天/一小时/一周内卖出的包子数量,我们能得到只有一段时间内事情发生的次数。
由于事情是随机发生的,也就是在统计的一定时间内,任意时刻都有可能发生,所以我们就要对二项式公式改进。假设一个小时内发生了 k k k次,如果我们10分钟统计一次,总共统计 n = 6 n=6 n=6次,我们期待 p = k n p=\frac{k}{n} p=nk,也就是 k k k次需要分别散落在6个10分钟内,显然 k k k次可能出现在一个10分钟内。那么1秒钟统计一次呢?还是不行,因为还是存在1秒钟发生 k k k次的可能性。为了保证单位时间内最多只有一次事件发生,泊松分布将 n → + ∞ n \rightarrow +\infty n→+∞,那么单次事件只能发生在 1 n \frac{1}{n} n1时间内。
我们可以统计出一段时间内出现的平均次数 λ \lambda λ,那么可以认为单次事件概率 p = λ n p=\frac{\lambda}{n} p=nλ,于是二项式分布就变成了:
lim n → ∞ P ( X = k ) = lim n → ∞ ( n k ) p k ( 1 − p ) n − k = ( λ k k ! ) exp ( − λ ) = λ k k ! e − λ \lim _{n \rightarrow \infty} P(X=k) \\ = \lim _{n \rightarrow \infty}\left(\begin{array}{l}n \\ k\end{array}\right) p^{k}(1-p)^{n-k}\\ = \left(\frac{\lambda^{k}}{k !}\right) \exp (-\lambda)\\ = \frac{\lambda^k}{k!}e^{-\lambda} n→∞limP(X=k)=n→∞lim(nk)pk(1−p)n−k=(k!λk)exp(−λ)=k!λke−λ
其实 e e e的定义就是(参见:自然常数e的含义):
lim n → + ∞ ( 1 + 1 n ) n \lim_{n \rightarrow +\infty}(1+\frac{1}{n})^n n→+∞lim(1+n1)n
而 e − λ = lim n → + ∞ ( 1 + − λ n ) n e^{-\lambda} = \lim_{n \rightarrow +\infty}(1+\frac{-\lambda}{n})^n e−λ=limn→+∞(1+n−λ)n。
最终泊松分布定义为:若 X X X服从参数为 λ \lambda λ的泊松分布,记为 X ∼ π ( λ ) X\sim \pi(\lambda) X∼π(λ)或 X ∼ P ( λ ) X\sim P(\lambda) X∼P(λ)。
P ( X = k ) = e − λ k ! λ k P(X=k)=\frac{e^{-\lambda}}{k !}\lambda^{k} P(X=k)=k!e−λλk
相关性质:
- E ( X ) = λ E(X) = \lambda E(X)=λ
- D ( X ) = λ D(X) = \lambda D(X)=λ
PMF与PDF
虽然 n → + ∞ n\rightarrow +\infty n→+∞,并且公式也可以计算 k > 0 k>0 k>0的非整数,但是泊松分布还是针对离散型随机变量,所以上述公式又称为泊松分布的PMF(概率质量函数)。
-
PMF(Probability Mass Function,概率质量函数): 是对离散随机变量的定义。是离散随机变量在各个特定取值的概率。该函数通俗来说,就是对于一个离散型概率事件来说,使用这个函数来求它的各个成功事件结果的概率。
-
PDF(Probability Density Function,概率密度函数 ):是对连续性随机变量的定义。与PMF不同的是,PDF在特定点上的值并不是该点的概率, 连续随机概率事件只能求一段区域内发生事件的概率, 通过对这段区间进行积分来求。通俗来说, 使用这个概率密度函数将想要求概率的区间的临界点(最大值和最小值)带入求积分,就是该区间的概率。
参数lambda
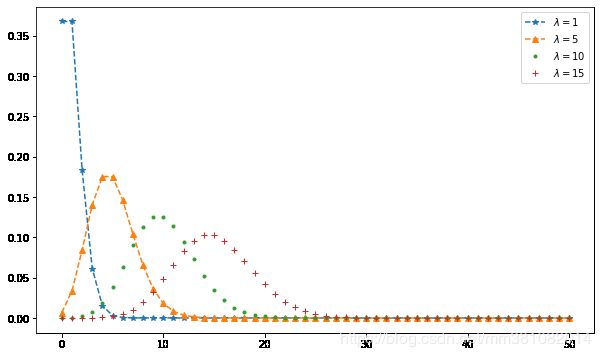
我们来看不同参数 λ \lambda λ的泊松分布情况。注意,由于是离散随机变量,所以我们对 k k k只能取 ≥ 0 \geq 0 ≥0的整数。
from scipy.special import factorial
Xs = np.linspace(0, 50, 51)
def PD(k, lmd):
return np.power(lmd, k) * np.exp(-lmd) / factorial(k)
plt.figure(figsize=(10, 6))
plt.plot(Xs, PD(Xs, lmd=1), '*--', label=rf'$\lambda=1$')
plt.plot(Xs, PD(Xs, lmd=5), '^--', label=rf'$\lambda=5$')
plt.plot(Xs, PD(Xs, lmd=10), '.', label=rf'$\lambda=10$')
plt.plot(Xs, PD(Xs, lmd=15), '+', label=rf'$\lambda=15$')
plt.legend()
plt.show()
从上图中,可以看出,泊松分布围绕着 λ \lambda λ为中心的,而且 λ \lambda λ越大,越对称,也越像正态分布。
与正态分布的关系
知乎上有个答案这样说的:
正态分布是所有分布趋于极限大样本的分布,属于连续分布。二项分布与泊松分布,则都是离散分布。二项分布的极限分布是泊松分布,泊松分布的极限分布是正态分布,即 n p = λ np=\lambda np=λ,当 n n n很大时,可以近似相等。当 n n n很大时(还没达到连续的程度),可以用泊松分布近似代替二项分布;当n再变大,几乎可以看成连续时,二项分布和泊松分布都可以用正态分布来代替!
乍一看,好像是这么回事,但是仔细想想我们本来就是假设 n → + ∞ n \rightarrow +\infty n→+∞。从上面的实验中我们发现, λ \lambda λ越大越接近正态分布。
简书上一篇blog认为:当发生次数 k k k比较大的时候,泊松分布会变成均值为 λ \lambda λ,方差为 λ \lambda λ的正态分布:
lim k → ∞ λ k k ! e − λ = 1 2 π λ e − ( x − λ ) 2 / 2 λ ∼ N ( λ , λ ) \lim _{k \rightarrow \infty} \frac{\lambda^{k}}{k !} e^{-\lambda}=\frac{1}{\sqrt{2 \pi \lambda}} e^{-(x-\lambda)^{2} / 2 \lambda} \sim N(\lambda, \lambda) k→∞limk!λke−λ=2πλ1e−(x−λ)2/2λ∼N(λ,λ)
个人认为这个结论也是明显不对,因为不论参数 λ \lambda λ, k k k都可以 → ∞ \rightarrow \infty →∞。不过后半句话应该是对的。
根据这篇数学文章上的图(截取如下),当 μ \mu μ也就是 λ → ∞ \lambda\rightarrow \infty λ→∞和 σ 2 = λ \sigma^{2}=\lambda σ2=λ时,变成了 N ( μ , σ ) N(\mu, \sigma) N(μ,σ):