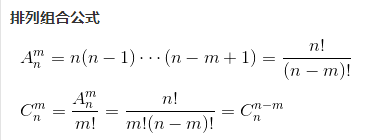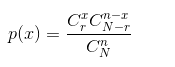概率统计（一）随机事件与随机变量

一、随机事件

本文为在学习概率统计中，进行的汇总

1.基本概念

在一定条件下，在个别试验或观察中呈现不确定性，但在大量重复试验或观察中其结果又具有一定规律性的现象，称为随机现象。
使随机现象得以实现和对它观察的全过程称为随机试验，记为E。

关于几个基础概念，以最常见的掷骰子为例进行说明：

1. 随机试验的所有可能结果组成的集合为样本空间，记为Ω：如Ω = {1,2,3,4,5,6}；
2. 试验的每一个可能结果称为样本点，记为ω：如ω1 = {1}，ω2 = {2}，ω3 = {3}；
3. 样本空间Ω中满足一定条件的子集为随机事件，用大写字母A、B、C…表示。（随机事件在随机试验中可能出现也可能不出现）：如A = {1,2,3}；
4. ；在试验中，一个事件发生是指构成该事件的一个样本点出现，由于样本空间Ω包含了所有的样本点，所以在每次试验中，它总是发生，因此称Ω为必然事件；
5. 空集φ不包含任何样本点，且在每次试验中总不发生，所以是不可能事件：如掷骰子出现的点数为7。

2.概率

事件A发生的几率。

同样以掷骰子为例，1,2,3,4,5,6出现的概率均为1/6，我们令A = {1,2}，B = {1,2,3}，根据性质则有

1. 对于任一事件A，均有P（~A） = 1 - P（A）
   P（~A） = 1 - P（A） = 1 - 1/3 = 2/3
2. 对于两个事件A和B，若A∈B，则有P（B - A） = P（B） - P（A），P（B） > P（A）
   P（B - A） = P（B） - P（A） = 1/2 - 1/3 = 1/6
3. 对于任意两个事件A和B，有P（A∪B） = P（A） + P（B） - P（A ∩ B）
   P（A∪B） = P（A） + P（B） - P（A ∩ B） = 1/3 + 1/2 -1/3 = 1/2

3.古典概型

首先需要复习一下排列组合的计算公式：

• 定义
  设随机事件E的样本空间中只有有限个样本点，即Ω = {ω₁，ω₂…}，其中n为样本点的总数，每个样本点出现的概率是相等的，并且每次试验有且仅有一个样本点发生，则称这类现象为古典概型。

• 举例
  假设有n个不同颜色的球，每个球以同样的概率1/m落到m个格子（m >= n）中，且每个格子可以容纳任意多个球，分别求出如下两个事件A和B的概率。

  A：指定的n个格子中各有一个球；
  由于每个球可以平均地落入m个格子中的任一个，并且每一个格子中可落入任意多个球，所以n个球落入m个格子中的分布情况相当于从m个格子中选取n个的可重复排列，故样本空间共有mⁿ种可能的基本结果，所以事件A所含基本结果数是n个球在指定的m个格子中的全排列数，即：
  P（A） = n！/ mⁿ

  B：存在k个格子，其中各有一个球；
  由于m个格子是可以任意选取的，故先从m个格子中任意选出n个来，那么选法共有C（m，n）种，对于每种选定的n个格子，有n！个几本结果，则有
  P（B） = C（m，n）* n！/ mⁿ = n！/ （mⁿ * （m - n）！）

• Python实现
  将上述例子应用到具体的问题中，概率论的历史上有一个颇为著名的生日问题：求n个同班同学没有两人生日相同的概率。
  如果把这n个同学看作上例中的n个球，而把一年365天看作格子，即m = 365，则上述的P（B）就是我们要求的概率，令n = 40。
  用Python实现古典概率的计算

#采用函数的递归方法计算阶乘
def factorial(n):
  	if n == 0:
  	   return 1;
  	else:
  	   return (n * factorial(n-1))

l_fac = factorial(365) #计算l的阶乘
l_k_fac = factorial(365 - 40) #l-k的阶乘
l_k_exp = 365**40 #l的k次方

p_b = l_fac / (l_k_fac * l_k_exp)
print("事件B的概率为：",p_b)
print("40个同学中至少两人同一天过生日的概率是：",1-p_b)

4.条件概率

• 定义
  设A和B是两个事件，且P（B） > 0，称P（A|B）= P（AB）/ P（B）为在事件B发生的条件下，事件A发生的概率。

• 举例
  某集体中有N个男人和M个女人，其中患色盲者男性n人，女性m人。我们用Ω表示该集体，A表示其中全体女性的集合，B表示其中全体色盲者的集合。如果从Ω中随意抽取一人，则这个人分别是女性、色盲者和既为女性又是色盲者的概率分别为：
  P（A） = M / （M + N）
  P（B） = （m + n） / （M + N）
  P（AB） = m / （M + N）
  如果限定只从女性中随机抽取一人（即事件A已发生），那么这个女人为色盲者的条件概率为
  P（B|A） = m / M = P（AB）/ P（A）

5.全概率公式和贝叶斯公式

概率的乘法公式：
P（AB） = P（B|A）P（A） = P（A|B）P（B）

• 全概率公式
  

• 贝叶斯公式
  

• 先验概率与后验概率
  先验概率：P（L_k）
  L_k视为导致试验结果A发生的原因，而P（L_k）表示各种原因发生的可能性大小，故称为先验概率
  后验概率：P（L_k| C）
  P（L_k| C）反应了当试验产生了结果A后，再对各种原因概率的新认识，故称为后验概率

• 两者的区别与联系
  全概率公式是已知第一阶段求第二阶段，比如第一阶段分A、B、C三种，然后A、B、C中均有D发生的概率，最后求D的概率
  P(D)=P(A)*P(D|A）+ P(B)*P(D|B）+ P©*P(D|C）
  贝叶斯公式是已知第二阶段反推第一阶段，跟上面建立的A、B、C、D模型一样，已知P(D)，求在A发生下D发生的概率
  P(A|D)=P(AD)/P(D)=P(A)*P(D|A)/P(D)

• 举例
  例题：甲乙两人独立对同一目标射击一次，命中率分别为50%和60%
  设事件A={甲中}，事件B={乙中}，事件C={命中}，P(A)=50%，P(B)=60%，C=A+B

  （1）甲乙同时射击，求命中率；
  P（C） = P(A+B) = P(A) + P(B) - P(AB) = P(A) + P(B) - P(A)P(B) = 0.8

  （2）甲乙先取一人，由其射击，求命中率；
  令A1 = {选甲}，A2 = {选乙}，则 P(A1)=1/2,P(A2)=1/2;
  P（C）= P(A1)P(C|A1) + P(A2)P(C|A2) = 0.55

  （3）甲乙先取一人，由其射击，已知目标被命中，求是甲命中的概率
  P(A1|C) = P(A1)P(C|A1)/[P(A1)P(C|A1) + P(A2)P(C|A2)]

原文链接：https://blog.csdn.net/chixuezhihun/article/details/51968612

二、随机变量

1.随机变量及其分布

• 随机变量定义

  随机变量是定义在样本空间Ω上，取值在实数域上的函数。由于它的自变量是随机试验的结果，而随机试验结果的出现具有随机性，因此随机变量的取值也具有一定的随机性。

• 随机变量的分布函数
  设X是一个随机变量，对任意的实数x，令F(x) = P{X <= x},x ∈ (-∞, +∞)，
  则称F(x)为随机变量x的分布函数，也称为概率累积函数。
  直观上看，分布函数F(x)是一个定义在(-∞, +∞)上的实值函数，F(x)在点x处取值为随机变量X落在区间(-∞, +x)上的概率，分布函数就是在一个区间范围内概率函数的累加，这个区间就是负无穷到当前节点。

2.离散型随机变量

如果随机变量X的全部可能取值只有有限多个或可列无穷多个，则称X为离散型随机变量。
掷骰子的结果就是离散型随机变量。

（1）二项分布（伯努利试验）

• 定义
  如果一个随机试验只有两种可能的结果A和~A，并且P(A) = p,P( ~A) = 1 - p = q,0 < p < 1，则称此试验为伯努利试验（Bernoulli），Bernoulli试验独立重复进行n次，称为n重伯努利试验。

• 举例
  从一批产品中检验次品，在其中进行有放回抽样n次，抽到次品称为“成功”，抽到正品称为“失败”，这就是n重伯努利试验。

• 分布函数
  上例中，设A = {n重伯努利试验中A出现k次}，一共抽了n次，k(k < n)次抽中了A，概率为p，k次则为p^k，n-k次抽中了非A，概率为1-p的组合的次数就是C(n,k)，则
  
  这就是著名的二项分布，常记作B(n, k)，当n=1时为二点分布，记为B(1, k)，其中
  均值：μ = np
  方差：δ² = npq

• 应用
  在知道某种实验结果概率的情况下，能够很好地推断试验次数后发生其中某一结果的概率

（2）超几何分布

• 定义
  超几何分布和二项分布比较相似，二项分布每次实验完全一样，而超几何分布前一次的实验结果会影响后面的实验结果。简单地讲，二项分布是有放回抽取，而超几何分布是无放回的抽取。

• 分布函数
  
  其中
  均值：μ = nr / N
  方差：δ² = r(N - r)n(N - n) / N²(N - 1)

• 举例
  在一个口袋中装有30个球，其中有10个红球，其余为白球，这些球除颜色外完全相同。游戏者一次从中摸出5个球。摸到至少4个红球就中一等奖，那么获一等奖的概率是多少？
  由题可知 N = 30，r = 10，n = 5，
  P（一等奖）= P(X = 4)+ P(X = 5) = 106 / 3933

（3）泊松分布

• 定义
  泊松分布适合于描述单位时间（或空间）内随机事件发生的次数。如某一服务设施在一定时间内到达的人数，电话交换机接到呼叫的次数，汽车站台的候客人数，机器出现的故障数，自然灾害发生的次数，一块产品上的缺陷数，显微镜下单位分区内的细菌分布数等等。

• 分布函数
  
  其中
  均值：μ = λ（单位时间内随机事件的平均发生率）
  方差：δ² = λ

• 应用
  泊松分布是二项分布中n很大而p很小的一种极限形式，可应用于某个时间范围内，发生某事件x次的概率是多大

3.连续型随机变量

（1）均匀分布

均匀概率分布是指连续随机变量所有可能出现值出现概率都相同。

• 分布函数
  
• Python实现

import numpy as np
from matplotlib import pyplot as plt
 
# 定义x的取值范围
# print(x) # -99-99
x = np.arange(-100, 100)
 
# 闭区间[a,b]上每个变量出现的概率相等
def uniform(x, a , b):
  # prob的取值要么是1/(b-a)，要么是0
  prob = [1/(b-a) if a <= v and v <= b else 0 for v in x]
  # 返回x,prob,以及随机变量出现概率的均值和方差
  return x, prob, np.mean(prob), np.std(prob)
 
# 给定两个区间,且这两个区间位于（-100, 100）内
list = [(-50, 50), (20, 30)]
for li in list:
  a, b = li[0], li[1]
  x, prob, m, s = uniform(x, a, b)
  # mu代表均值u,sigma代表标准差
  plt.plot(x, prob, label=r'$\mu=%.2f,\ \sigma=%.2f$' %(m ,s))
 
# 画出两个子区间均匀分布的图形
plt.legend()
plt.savefig('./uniform.png')
plt.show()

（2）正态分布

• 定义
  正态分布又称高斯分布，是统计学中常见的一种分布，表现为两边对称，是一种钟型的概率分布，其概率密度图为：
  
  分布函数：
  
  其中
  μ是正态随机变量的均值；δ是标准差； π是圆周率，约等于3.1416··· ；e=2.71828⋅⋅⋅
  特别的，当μ=0且δ=1的正态分布，被称为标准正态分布。

• 如何来确定数据是否正态分布，主要有以下几种方法：

1. 图形感受法：建立直方图或者枝干图，看图像的形状是否类似正态曲线，既土墩形或者钟形，并且两端对称。
2. 计算区间μ ± δ、μ ± 2δ、μ ± 3δ，看落在区间的百分比是否近似于68%，95%，100%。（切比雪夫法则和经验法则）
3. 求IQR和标准差s，计算IQR/s，如若是正态分布，则IQR/s≈1.3.
4. 建立正态概率图，如果近似正态分布，点会落在一条直线上。

• 正态分布为什么常见：
  真正原因是中心极限定理。
  根据中心极限定理，如果一个事物受到多种因素的影响，不管每个因素本身服从什么分布，它们加总后，结果的平均值是正态分布的。

（3）指数分布

• 指数分布是描述泊松分布中事件发生时间间隔的概率分布。

• 指数分布有如下的适用条件：

1. x是两个事件发生之间的时间间隔，并且x>0;
2. 事件之间是相互独立的；
3. 事件发生的频率是稳定的；
4. 两个事件不能发生在同一瞬间。

• 这几个条件实质上也是使用泊松分布的前提条件。如果满足上述条件，则x是一个指数随机变量，x的分布是一个指数分布。如果不满足上述条件，那么需要使用Weibull分布或者gamma分布。

4.随机变量的数字特征

（1） 数学期望

数学期望代表了随机变量取值的平均值。

数学期望的性质：
（1）若c是常数，则E© = c；
（2）E(aX + bY) = aE(X) + bE(Y)，其中a、b为任意常数；
（3）若X、Y相互独立，则E(XY) = E(X) E(Y) 。

（2） 方差

方差是用来描述随机变量取值相对于均值的离散程度的一个量。

方差性质：
（1）若c是常数，则Var© = 0；
（2）Var(aX + b) = a²Var(X)，其中a、b为任意常数；
（3）若X、Y相互独立，则Var(X + Y) = Var(X) + Var(Y)。

（3）协方差

协方差和相关系数都是描述随机变量X与随机变量Y之间的线性联系成都的数字量。

协方差的性质：
（1）Cov(X, Y) = Cov(Y, X)；
（2）Cov(aX + b, cY + d) = acCov(X, Y)，其中a、b、c、d为任意常数；
（3）Cov(X₁ + X₂, Y) = Cov(X₁, Y) + Cov(X₂, Y) ；
（4）Cov(X, Y) = E(X, Y) - E(X) E(Y)，当X、Y相互独立时，有Cov(X, Y) = 0；
（5）Cov(X, X) = Var(X)。

（4）相关系数