吴恩达机器学习第二周学习笔记及编程作业答案

吴恩达机器学习第二周学习笔记及编程作业答案

一、理论基础
1、机器学习定义：一个程序被认为能从经验 E 中学习，解决任务 T，达到性能度量值P，当且仅当，有了经验 E 后，经过 P 评判，程序在处理 T 时的性能有所提升

机器学习都可以分为两大类：监督学习；无监督学习。

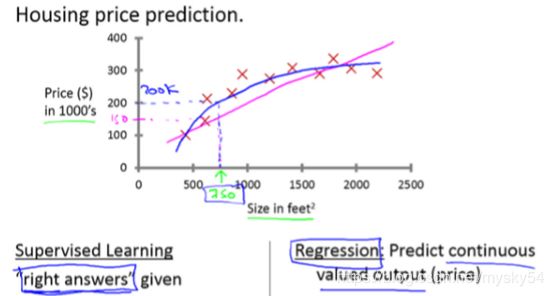
监督学习：在监督学习中，我们会得到一个数据集，并且已经知道我们的正确输出应该是什么样子的，因为我们认为输入和输出之间是有关系的。

监督学习问题分为回归问题和分类问题。在回归问题中，我们试图在连续输出中预测结果，这意味着我们试图将输入变量映射到某个连续函数。在分类问题中，我们试图预测离散输出的结果。换句话说，我们试图将输入变量映射到离散类别中。

无监督学习：无监督的学习使我们能够在很少或根本不知道我们的结果应该是什么的情况下处理问题。我们可以从数据中导出结构，在这些数据中，我们不一定知道变量的影响。

监督学习问题实例：垃圾邮件分类问题；糖尿病、乳腺癌良、恶性问题

无监督学习问题实例：谷歌新闻的例子；细分市场的例子

2、单变量线性回归(Linear Regression with One Variable)

2.1建模误差（modeling error）：模型所预测的值与训练集中实际值之间的差距

代价函数公式：


2.2.梯度下降

梯度下降是一个用来求函数最小值的算法，我们将使用梯度下降算法来求出代价函数J的最小值。

梯度下降思想是：开始时我们随机选择一个参数的组合，计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到到到一个局部最小值（local minimum），因为我们并没有尝试完所有的参数组合，所以不能确定我们得到的局部最小值是否便是全局最小值（global minimum），选择不同的初始参数组合，可能会找到不同的局部最小值。

批量梯度下降（batch gradient descent）算法的公式为：

其中α是学习率（learning rate），它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大，在批量梯度下降中，我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。

注释：如果α太小，它会需要很多步才能到达全局最低点。如果α太大，那么梯度下降法可能会越过最低点，甚至可能无法收敛。学习速率α保持不变时，梯度下降也可以收敛到局部最低点（刚开始就处于局部最低点的时候，α将不会影响）。

注：同时更新θ1和θ2；



多变量梯度下降：


梯度下降法实践 1-特征缩放


在运行梯度下降算法之前，进行特征缩放依旧是非常必要的。

梯度下降法实践 2-学习率

梯度下降算法的每次迭代受到学习率的影响，如果学习率过小，则达到收敛所需的迭代次数会非常高；如果学习率过大，每次迭代可能不会减小代价函数，可能会越过局部最小值导致无法收敛。

正规方程

梯度下降与正规方程的比较：

只要特征变量数量小于一万，我通常使用标准方程法，而不使用梯度下降法，梯度下降法可以用在有大量特征变量的线性回归问题。

二、编程作业
1.warmUpExercise.m（Simple
example function in Octave/MATLAB）：实现5×5的单位矩阵

function A = warmUpExercise()  
A = [];  
A=eye(5);  

2.plotData.m（Function to display the dataset）：implement linear regression with one variable to predict
profits for a food truck.

The file ex1data1.txt contains the dataset for our linear
regression problem. The first column is the population of a city and the second column is the profit of a food truck in that city.
use a scatter plot（散点图） to visualize the data, since it has only two properties to plot (profit and population).

unction plotData(x, y)    
figure; % open a new figure window  
ta=load('ex1data1.txt');  
x=data(:,1);%读取矩阵的第一列  
y=data(:,2);%读取矩阵的第二列  
%m=length(y);      
%To change the markers to red “x”, we used the option ‘rx’ together with the plot command, i.e., plot(..,[your options here],.., ‘rx’); )  
  %用rx将我们选择的内容变成红色  
 plot(x, y, 'rx', 'MarkerSize', 10);  %10表示标记点的大小
xlabel('Population of City in 10,000s');% set the x-axis label  
ylabel('Profit in $10,000s');% set the y-axis label 

3. gradientDescent.m（Function to run gradient descent）：fit the linear regression parameters θ to our dataset
using gradient descent

The objective of linear regression is to minimize the
cost function

where the hypothesis hθ(x) is given by the linear model

minimize cost J(θ). One way to do this is to use the
batch gradient descent algorithm（批量梯度下降算法）.In batch gradient descent, each iteration performs the update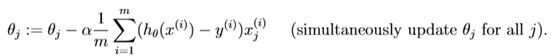

function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)  
Initialize some useful values  
m = length(y); % number of training examples    
J_history = zeros(num_iters, 1);  
for iter = 1:num_iters  
 theta = theta - alpha/length(y)*(X'*(X*theta-y));  
    % Save the cost J in every iteration        
J_history(iter) = computeCost(X, y, theta);  
end  
end  

解释：(X’(Xtheta-y))中X需要转置一下的原因是因为需要乘以X的列向量，因为theta是列向量
4.computeCost.m（Function to compute the cost of linear regression）：implement a function to calculate J(θ) so you can check the convergence of your gradient descent implementation.
代价函数公式如下：

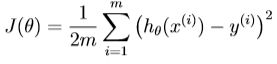
function J = computeCost(X, y, theta)  
Initialize some useful values  
m = length(y); % number of training examples  
J = 0;  
sum((X * theta - y) .^ 2) / (2*m);%theta为列向量，用X的每一行去乘以theta 
end  

解释：(X * theta - y) 是因为theta为列向量，用X的每一行去乘以theta