法线贴图技术原理与实践
目录
- Blinn-Phong光照模型中的法线
- 法线贴图让每个片元都有独立的法线
- 法线存储在什么坐标空间?
- 世界空间
- 模型空间
- 切线空间
- 将向量在切线空间和世界空间之间变换
- 从切线空间变换到世界空间
- 从世界空间变换到切线空间
- 存储切线空间法线到贴图
- 切线空间法线贴图中存的是什么?
- 法线和RGB之间的映射
- 为什么切线空间的法线贴图是偏蓝色?
- 法线贴图压缩
- 计算模型的顶点切线
- 使用法线贴图计算光照
- 在切线空间中计算
- 在世界空间中计算
- 参考资料
Blinn-Phong光照模型中的法线
在Blinn-Phong光照模型中,法线用于计算漫反射diffuse颜色和镜面高光specular颜色。有两种着色模型,逐顶点的高洛德着色(Gouraud Shading)和逐像素的Phong Shading。使用Gouraud Shading时,在vertex shader中,使用每个顶点的法线计算该顶点的diffuse和specular,然后在片元上插值。使用Phong Shading时,在fragment shader中,使用插值后的逐片元的法线计算该片元的diffuse和specular。使用顶点级的法线是很粗糙的,因为对于低模,顶点数量有限,导致物体上使用法线计算出来的明暗的变化没那么细致;而使用插值后的法线虽然效果要好一些,但是仍然缺少细节,因为法线是插值得到的,顶点之间的片元的法线只能是从顶点法线光滑过渡得到,无法体现出丰富的方向。如果使用高模,则由于顶点数足够多,通过光照可以得到比较丰富的明暗细节。
法线贴图让每个片元都有独立的法线
高模虽然顶点够多,细节够丰富,但是渲染开销太大。其实我们仅仅通过增加法线数量就可以得到比较丰富的明暗细节,在一定程度上达到高模的渲染效果。因此诞生了法线贴图技术,将高模的法线细节保存到一张贴图上,给低模使用。在片元着色器中,通过采样法线贴图,让每个片元都有自己独立的法线。这样每个片元都可以独立计算出光照明暗。效果比法线插值好得多。
法线存储在什么坐标空间?
既然要把法线存储到贴图中,那么使用哪个坐标空间的法线呢?
世界空间
因为光照往往在世界空间计算,一种想法是把世界空间的法线保存到法线贴图中。然而这样做法线的方向就定死了,物体只要一旋转或非等比缩放,其顶点法线向量的世界坐标就要变化,这样就不能使用预先计算好的世界空间的法线了。
模型空间
那么使用模型空间的法线行不行呢?毕竟顶点法线数据就是模型空间的。这样仍然不够灵活。比如一个立方体的六个面就需要六张法线贴图,即便他们的细节是一样的,但是对于每个面,其在模型空间中法线的朝向是不同的。
切线空间
图形学的前辈们想到了一个灵活的方法,将法线存储到切线空间。那么什么是切线空间呢?切线空间是每个顶点上的独立的坐标系,有TBN三个轴,其中N为顶点的法线,而T,B分别为顶点的切线和副切线。对于TBN坐标系,T是X轴,B是Y轴,N是Z轴。每个顶点的TBN坐标系都不一样。如何在模型空间中确定每个顶点的TBN坐标系的朝向呢?(TBN坐标系原点所在的位置就是顶点的位置,一般不需要关心,因为我们只变换方向)。对于N好办,就是顶点的法线方向。而T和B互相垂直,且位于和N垂直的平面内,这个平面内互相垂直的向量有无数组,那么如何确定T和B呢?
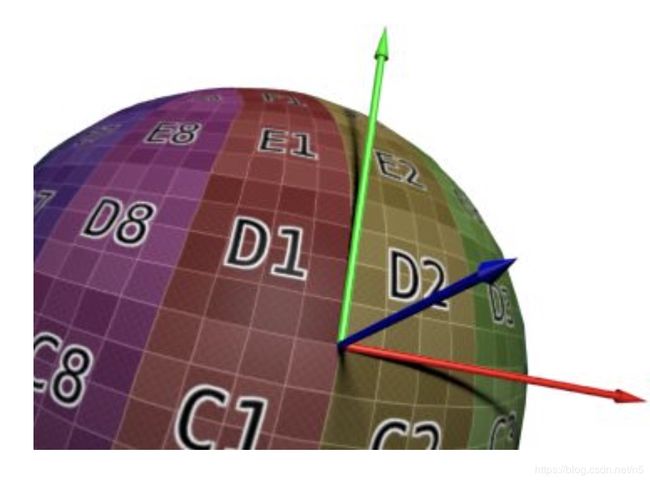
考虑到顶点的UV坐标恰好沿着互相垂直的两个轴定义,所以我们可以沿着UV坐标变化的方向确定T和B的方向。下面会说如何计算顶点的切线和副切线。另外某些文章会说切线空间是定义在三角形上的,这个没错,法线和切线本身就是针对面来说的,一个点并不存在法线。不过为了使用VS和FS进行光照计算,我们才平均出了顶点法线,切线也是一样的道理。如果某套渲染系统是以面为单位进行渲染的,我们只需要计算出面的法线和切线。
将向量在切线空间和世界空间之间变换
TBN坐标系中,N是坐标系的z轴,因此N的值就是(0,0,1)。尽管每个顶点具有不同的模型空间的法线,但切线空间中的顶点法线N就是Z轴,因为切线空间就是这么定义的。同样,TBN坐标系中,切线T是x轴(1,0,0),副切线B是y轴(0,1,0)。可以将切线空间理解为模型空间的子坐标系,而每个顶点都有一个独立的切线空间坐标系。理解了这一点,才能理解如何构建切线空间和世界空间之间的变换矩阵。但是并非切线空间中所有的片元的法线都是对齐Z轴的,只有当片元法线和顶点法线方向一致是才是,其他的片元法线方向是偏离开Z轴的。
从切线空间变换到世界空间
切线空间中,切线T是X轴,副切线B是Y轴,法线N是Z轴,这个三个向量都是单位向量。而我们定义在模型数据中的顶点的法线和切线都是在模型空间中的,而副切线可以由法线和切线的叉乘得到。根据空间变换矩阵的构造方法,对于向量右乘约定,构造一个3x3向量空间变换矩阵,将空间B中表示的空间A的三个轴,填入3x3矩阵的三个列,就得到了空间A到空间B的变换矩阵。(参考:谈一谈3D编程中的矩阵)因为切线空间的这三个向量都是单位向量,而他们在模型空间中的值可认为是将单位向量从切线空间变换到模型空间后得到,那么将模型空间的T,B,N作为矩阵的三个列即可得到切线空间到模型空间的变换矩阵。同样,为了得到切线空间到世界空间的变换矩阵,我们先将模型空间下的顶点切线,副切线和法线变换到世界空间,然后将世界空间的这三个向量填入矩阵的三列,就得到了切线空间到世界空间的变换矩阵。
glsl中的例子:
vec3 worldNormal = normalize(a_Normal * mat3(u_world2Object));
vec3 worldTangent = normalize(u_object2World*a_Tangent).xyz;
vec3 worldBinormal = cross(worldNormal, worldTangent) * a_Tangent.w;
//将TBN向量按列放入矩阵,构造出tangentToWorld矩阵
//注意glsl中mat3是列主的
mat3 tangentToWorld = mat3(worldTangent, worldBinormal, worldNormal);
从世界空间变换到切线空间
因为我们构造的是坐标系的变换矩阵,这是一个纯旋转矩阵,也是正交矩阵。因此逆矩阵就是转置矩阵。所以从世界空间变换到切线空间的矩阵,就是从切线空间变换到世界空间的矩阵的转置矩阵。对于向量右乘约定下的矩阵,我们将世界空间中的T,B,N向量按行填入矩阵即可。
//将TBN向量按行放入矩阵,构造出worldToTangent矩阵
//注意glsl中mat3是列主的
mat3 worldToTangent = mat3(worldTangent.x, worldBinormal.x, worldNormal.x,
worldTangent.y, worldBinormal.y, worldNormal.y,
worldTangent.z, worldBinormal.z, worldNormal.z);
存储切线空间法线到贴图
切线空间法线贴图中存的是什么?
需要认识到,切线空间的法线贴图中存储的是切线空间的法线。但是这并不是低模顶点的那些TBN空间中的N,那些N其实都是z轴,是(0,0,1),如果只有那些,是没有意义的。法线贴图的意义在于提供了远多于顶点数目的法线。比如可以从高模得到这些法线,然后将其转换到切线空间,这些法线就不是低模某个顶点的TBN空间的Z轴了,如果变换到这个顶点的TBN中,他就是一个偏离Z轴的方向。所以说,法线贴图存放的是对法线的扰动,如果某个片元没有扰动,法线值就是(0,0,1),代表了顶点原本的法线。如果有扰动,法线值在TBN空间中就是一个从Z轴偏移的方向,在模型空间中就是一个从顶点法线偏移的方向。
法线和RGB之间的映射
因为法线向量x,y,z的范围为[-1,1],而贴图颜色R,G,B的范围是[0,1],因此需要进行一个简单的映射,即 R|G|B = (x|y|z + 1)*0.5。
为什么切线空间的法线贴图是偏蓝色?
对于某个片元,当法线贴图没有对其法线进行扰动时,切线空间的法线值是(0,0,1),映射到RGB是(0.5,0.5,1),这是一种浅蓝色。当存在扰动时,基本上也只是x,y分量有一些偏移,幅度不会特别大,因此整个切线空间的法线贴图看上去是偏蓝色的。
法线贴图压缩
因为切线空间的法线都是朝向平面外的,z值总为正,因此可以只保存x,y,然后通过z=sqrt(1-(x*x+y*y))计算出z。
计算模型的顶点切线
模型数据不一定自带顶点切线数据,所以往往需要自己计算出顶点的切线。类似于法线的计算,我们先计算出三角面的切线,然后对于顶点,计算其所属的各个面的切线的平均值。那么如何计算出三角面的切线呢?简单介绍一下原理。
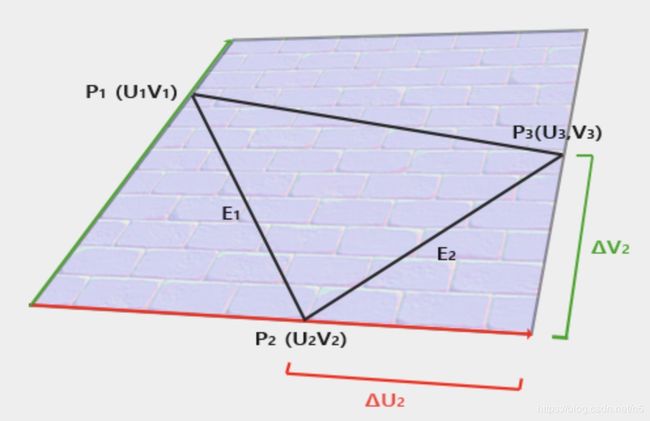
在上图中,红色向量为切线T,绿色为副切线B。因为T和B是TB平面的坐标轴,因此可以用T和B线性表出E1和E2:
E1 = deltaU1 * T + deltaV1 * B
E2 = deltaU2 * T + deltaV2 * B
而在模型空间中,E1和E2可以由顶点坐标计算出来,代入上式左边后,得到了一组线性方程,可以转化成矩阵乘法并通过计算逆矩阵就可以获得T和B。
参考代码:
static _calcFaceTangent(p0, p1, p2, uv0, uv1, uv2){
let edge1 = Vector3.sub(p1, p0, new Vector3());
let edge2 = Vector3.sub(p2, p0, new Vector3());
let deltaUV1 = Vector3.sub(uv1, uv0, new Vector3());
let deltaUV2 = Vector3.sub(uv2, uv0, new Vector3());
let f = 1.0 / (deltaUV1.x * deltaUV2.y - deltaUV2.x * deltaUV1.y);
let tangent = new Vector3();
tangent.x = f * (deltaUV2.y * edge1.x - deltaUV1.y * edge2.x);
tangent.y = f * (deltaUV2.y * edge1.y - deltaUV1.y * edge2.y);
tangent.z = f * (deltaUV2.y * edge1.z - deltaUV1.y * edge2.z);
tangent.normalize();
//compute binormal
let binormal = new Vector3();
binormal.x = f * (-deltaUV2.x * edge1.x + deltaUV1.x * edge2.x);
binormal.y = f * (-deltaUV2.x * edge1.y + deltaUV1.x * edge2.y);
binormal.z = f * (-deltaUV2.x * edge1.z + deltaUV1.x * edge2.z);
binormal.normalize();
//计算tangent和binormal的叉积,如果得到的向量和normal是反向的
//则将tangent.w设置为-1,在shader里面用这个w将计算出来的binormal反向
//注:这儿计算的并不会反向,但是如果是外部导入的切线,计算时的坐标系的手向不同是可能反向的
//保留这段代码主要是演示作用,此处计算的tanget的w总是1
let crossTB = new Vector3();
Vector3.cross(tangent, binormal, crossTB);
let normal = new Vector3();
Vector3.cross(edge1, edge2, normal);
if(Vector3.dot(crossTB, normal)<0){
tangent.w = -1;
} else {
tangent.w = 1;
}
return tangent;
}
实际上只需要计算切线即可,副切线在shader中通过法线和切线的叉乘计算。但是一般会根据手向性计算出切线的w值为-1或1。用于计算副切线时确定方向。
使用法线贴图计算光照
经过上面的讨论,我们弄明白了切线空间是什么,法线贴图中存储的是啥,为什么使用切线空间,以及如何在切线空间和世界空间之间进行变换。并且我们还简单了解了如何计算出模型的顶点切线。现在我们只需从法线贴图中获取到片元的法线,然后将光照需要的向量变换到一个统一的空间,就可以基于法线贴图进行光照计算。那么一般有两个方案,在切线空间计算以及在世界空间计算。
在切线空间中计算
因为法线贴图中存储的就是切线空间的法线,因此只要将光线方向和视线方向变换到切线空间就可以进行光照计算。而变换光线和视线可以在VS中完成,效率较高。然后在FS中,从法线贴图中获取切线空间的法线,并在切线空间中计算光照。这个方法中,需要将世界空间的光线方向和视线方向变换到切线空间,因此需要计算世界空间到切线空间的变换矩阵,这在上面已经讨论过。另外从法线贴图中获取法线,需要从RGB空间转换到向量空间,而法线在存储时进行了向量到RGB的映射,因此此处需要反映射。另外如果法线贴图是压缩存储的,还需要解压。
WebGL1.0/OpenGL ES2.x glsl shader代码:
- vertex shader
attribute vec4 a_Position;
attribute vec3 a_Normal;
attribute vec4 a_Tangent;
attribute vec2 a_Texcoord;
uniform mat4 u_mvpMatrix;
uniform mat4 u_object2World;
uniform mat4 u_world2Object;
uniform vec4 u_texMain_ST; // Main texture tiling and offset
uniform vec4 u_normalMap_ST; // Normal map tiling and offset
uniform vec3 u_worldCameraPos; // world space camera position
uniform vec4 u_worldLightPos; // World space light direction or position, if w==0 the light is directional
varying vec3 v_tangentLightDir; // tangent space light dir
varying vec3 v_tangentViewDir; // tangent space view dir
varying vec4 v_texcoord;
varying float v_atten;
void main(){
gl_Position = u_mvpMatrix * a_Position;
v_texcoord.xy = a_Texcoord.xy * u_texMain_ST.xy + u_texMain_ST.zw;
v_texcoord.zw = a_Texcoord.xy * u_normalMap_ST.xy + u_normalMap_ST.zw;
vec3 worldNormal = normalize(a_Normal * mat3(u_world2Object));
vec3 worldTangent = normalize(u_object2World*a_Tangent).xyz;
vec3 worldBinormal = cross(worldNormal, worldTangent) * a_Tangent.w;
//将TBN向量按行放入矩阵,构造出worldToTangent矩阵
//注意glsl中mat3是列主的
mat3 worldToTangent = mat3(worldTangent.x, worldBinormal.x, worldNormal.x,
worldTangent.y, worldBinormal.y, worldNormal.y,
worldTangent.z, worldBinormal.z, worldNormal.z);
vec4 worldPos = u_object2World*a_Position;
vec3 worldViewDir = normalize(u_worldCameraPos - worldPos.xyz);
v_tangentViewDir = worldToTangent * worldViewDir;
vec3 worldLightDir;
v_atten = 1.0;
if(u_worldLightPos.w==1.0){ //点光源
vec3 lightver = u_worldLightPos.xyz - worldPos.xyz;
float dis = length(lightver);
worldLightDir = normalize(lightver);
vec3 a = vec3(0.01);
v_atten = 1.0/(a.x + a.y*dis + a.z*dis*dis);
} else {
worldLightDir = normalize(u_worldLightPos.xyz);
}
v_tangentLightDir = worldToTangent * worldLightDir;
}
- fragment shader
#ifdef GL_ES
precision mediump float;
#endif
uniform vec3 u_LightColor; // Light color
uniform sampler2D u_texMain;
uniform sampler2D u_normalMap;
uniform vec3 u_colorTint;
#ifdef USE_AMBIENT
uniform vec3 u_ambient; // scene ambient
#endif
uniform vec3 u_specular; // specular
uniform float u_gloss; //gloss
varying vec3 v_tangentLightDir; // tangent space light dir
varying vec3 v_tangentViewDir; // tangent space view dir
varying vec4 v_texcoord;
varying float v_atten;
void main(){
vec3 tangentLightDir = normalize(v_tangentLightDir);
vec3 tangentViewDir = normalize(v_tangentViewDir);
#ifdef PACK_NORMAL_MAP
vec4 packedNormal = texture2D(u_normalMap, v_texcoord.zw);
vec3 tangentNormal;
tangentNormal.xy = packedNormal.xy * 2.0 - 1.0;
tangentNormal.z = sqrt(1.0 - clamp(dot(tangentNormal.xy, tangentNormal.xy), 0.0, 1.0));
#else
vec3 tangentNormal = texture2D(u_normalMap, v_texcoord.zw).xyz * 2.0 - 1.0;
#endif
vec3 albedo = texture2D(u_texMain, v_texcoord.xy).rgb * u_colorTint;
vec3 diffuse = u_LightColor * albedo * max(0.0, dot(tangentNormal, tangentLightDir));
#ifdef LIGHT_MODEL_PHONG
vec3 reflectDir = normalize(reflect(-tangentLightDir, tangentNormal));
vec3 specular = u_LightColor * u_specular * pow(max(0.0, dot(reflectDir,tangentViewDir)), u_gloss);
#else
vec3 halfDir = normalize(tangentLightDir + tangentViewDir);
vec3 specular = u_LightColor * u_specular * pow(max(0.0, dot(tangentNormal,halfDir)), u_gloss);
#endif
#ifdef USE_AMBIENT
vec3 ambient = u_ambient * albedo;
gl_FragColor = vec4(ambient + (diffuse + specular) * v_atten, 1.0);
#else
gl_FragColor = vec4((diffuse + specular) * v_atten, 1.0);
#endif
}
在世界空间中计算
在切线空间计算光照很方便,但是有时需要在世界空间做某些计算,例如采样cube map实现反射,这样就需要在世界空间进行光照。那么我们需要将所有的向量统一到世界空间,因为光线方向,视线方向通常都是在世界空间计算出来的,我们主要需要把法线贴图中的切线空间的法线变换到世界空间,因此我们需要切线空间到世界空间的变换矩阵,这在上面也已经推导过了,我们在VS中计算这个矩阵,并将这个矩阵传到FS中。而其他的计算方法和在切线空间是一样的。这里直接给出参考的WebGL1.0/OpenGLES2.x的glsl shader代码:
- vertex shader
attribute vec4 a_Position;
attribute vec3 a_Normal;
attribute vec4 a_Tangent;
attribute vec2 a_Texcoord;
uniform mat4 u_mvpMatrix;
uniform mat4 u_object2World;
uniform mat4 u_world2Object;
uniform vec4 u_texMain_ST; // Main texture tiling and offset
uniform vec4 u_normalMap_ST; // Normal map tiling and offset
// Tangent to World 3x3 matrix and worldPos
// 每个vec4的xyz是矩阵的一行,w存放了worldPos
varying vec4 v_TtoW0;
varying vec4 v_TtoW1;
varying vec4 v_TtoW2;
varying vec4 v_texcoord;
void main(){
gl_Position = u_mvpMatrix * a_Position;
v_texcoord.xy = a_Texcoord.xy * u_texMain_ST.xy + u_texMain_ST.zw;
v_texcoord.zw = a_Texcoord.xy * u_normalMap_ST.xy + u_normalMap_ST.zw;
vec3 worldNormal = normalize(a_Normal * mat3(u_world2Object));
vec3 worldTangent = normalize(u_object2World*a_Tangent).xyz;
vec3 worldBinormal = cross(worldNormal, worldTangent) * a_Tangent.w;
vec4 worldPos = u_object2World*a_Position;
//TBN向量按列放入矩阵,构造出 TangentToWorld矩阵,使用三个向量保存矩阵的三行,传入fs
//同时将worldPos存入三个向量的w中
v_TtoW0 = vec4(worldTangent.x, worldBinormal.x, worldNormal.x, worldPos.x);
v_TtoW1 = vec4(worldTangent.y, worldBinormal.y, worldNormal.y, worldPos.y);
v_TtoW2 = vec4(worldTangent.z, worldBinormal.z, worldNormal.z, worldPos.z);
}
- fragment shader
#ifdef GL_ES
precision mediump float;
#endif
uniform vec3 u_LightColor; // Light color
uniform sampler2D u_texMain;
uniform sampler2D u_normalMap;
uniform vec3 u_worldCameraPos; // world space camera position
uniform vec4 u_worldLightPos; // World space light direction or position, if w==0 the light is directional
uniform vec3 u_colorTint;
#ifdef USE_AMBIENT
uniform vec3 u_ambient; // scene ambient
#endif
uniform vec3 u_specular; // specular
uniform float u_gloss; //gloss
varying vec4 v_TtoW0;
varying vec4 v_TtoW1;
varying vec4 v_TtoW2;
varying vec4 v_texcoord;
void main(){
vec3 worldPos = vec3(v_TtoW0.w, v_TtoW1.w, v_TtoW2.w);
vec3 worldViewDir = normalize(u_worldCameraPos - worldPos.xyz);
vec3 worldLightDir;
float atten = 1.0;
if(u_worldLightPos.w==1.0){ //点光源
vec3 lightver = u_worldLightPos.xyz - worldPos.xyz;
float dis = length(lightver);
worldLightDir = normalize(lightver);
vec3 a = vec3(0.01);
atten = 1.0/(a.x + a.y*dis + a.z*dis*dis);
} else {
worldLightDir = normalize(u_worldLightPos.xyz);
}
#ifdef PACK_NORMAL_MAP
vec4 packedNormal = texture2D(u_normalMap, v_texcoord.zw);
vec3 normal;
normal.xy = packedNormal.xy * 2.0 - 1.0;
normal.z = sqrt(1.0 - clamp(dot(normal.xy, normal.xy), 0.0, 1.0));
#else
vec3 normal = texture2D(u_normalMap, v_texcoord.zw).xyz * 2.0 - 1.0;
#endif
//Transform the normal from tangent space to world space
normal = normalize(vec3(dot(v_TtoW0.xyz, normal), dot(v_TtoW1.xyz, normal), dot(v_TtoW2.xyz, normal)));
vec3 albedo = texture2D(u_texMain, v_texcoord.xy).rgb * u_colorTint;
vec3 diffuse = u_LightColor * albedo * max(0.0, dot(normal, worldLightDir));
#ifdef LIGHT_MODEL_PHONG
vec3 reflectDir = normalize(reflect(-worldLightDir, normal));
vec3 specular = u_LightColor * u_specular * pow(max(0.0, dot(reflectDir,worldViewDir)), u_gloss);
#else
vec3 halfDir = normalize(worldLightDir + worldViewDir);
vec3 specular = u_LightColor * u_specular * pow(max(0.0, dot(normal,halfDir)), u_gloss);
#endif
#ifdef USE_AMBIENT
vec3 ambient = u_ambient * albedo;
gl_FragColor = vec4(ambient + (diffuse + specular) * atten, 1.0);
#else
gl_FragColor = vec4((diffuse + specular) * atten, 1.0);
#endif
}
参考资料
- 《Unity Shader入门精要》
- LearnOpenGL - Normal Mapping
